龔健

　　(廣州鐵路職業技術學院，廣東 廣州 510430)

　　摘要：傳統無線傳感網絡定位算法沒有考慮節點移動問題，采用多次測量、推算節點運動軌跡方式估算節點位置，定位偏差偏大。針對節點移動會對周圍信號產生波動和多普勒頻移，提出一種基于移動節點信號衰減漸變模型，利用極大似然估計算法思想將移動節點對周圍RSSI指紋參量影響轉變為概率事件，并通過泰勒級數修正漸變模型。仿真實驗證明，新算法既可以減少對移動節點定位偏差，又可以有效彌補RSSI易受環境干擾的不足。

　　關鍵詞：極大似然估計算法；泰勒級數；接收信號強度指示；衰減漸變模型

0引言

　　在無線傳感網絡中，路徑傳播損耗定位算法屬于測距算法，首先根據信號強度與傳播距離損耗規律建立衰減模型，再依據實測節點信號強度測算之間距離，通過多邊測量、圓周或雙曲線函數計算節點位置［12］。RSSI接收信號強度指示算法屬于非測距算法，節點通過采集的信號參數與指紋數據庫進行最近匹配，從而估算節點位置。然而這兩類算法都沒有考慮到節點移動問題［3］。在實際工程中，錨節點位置通常會隨環境變化而移動，如對大氣、洋流的監測，如何利用現有設施實現對移動節點的精確定位是目前無線傳感網絡研究的難點和熱點。

　　目前業界對移動節點定位研究尚不成熟［45］。為避免算法過于復雜，一般采用多次測量，推算運動軌跡方法，以時間換取空間計算的復雜度。由于每次節點定位都存在誤差，很難描述節點真實運動狀態［6］，因此多次測量方法定位偏差較大，難以滿足真實工程需求。RSSI算法對靜止節點定位精確，但易受信號波動和多徑衰減影響，同時錨節點移動會對周圍信號產生信號波動和多普勒頻移［7］。如圖1所示，在RSSI算法模型中，節點隨機運動，速率越大，定位偏差也越大，若簡單地根據RSSI指紋數據庫最近匹配原則計算節點位置勢必產生較大誤差。

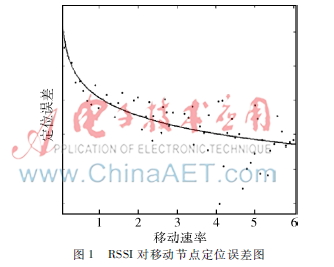
　　有鑒于此，本文提出一種基于移動節點信號衰減漸變模型，利用極大似然估計算法思想將移動節點對周圍RSSI指紋參量影響轉變為概率事件，并通過泰勒級數修正漸變模型，推導移動速率對定位誤差的關系和影響，既可以提高對移動節點定位的精確性，又可以彌補RSSI易受環境干擾的不足。

1極大似然估計算法

　　極大似然估計算法由德國數學家GAUSS C F提出，本質上是概率論在統計學中的應用［8］，目前已成為圖2極大似然算法原理圖無線傳感網絡測距算法之一，其概率統計定位原理如圖2所示。

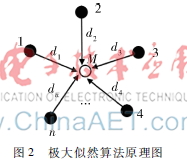
　　設目的節點M坐標為(x,y)，附近錨節點1，2，3，…，n的坐標分別為(x1,y1),(x2,y2),(x3,y3)，…,(xn,yn)，它們與節點M距離分別為d1，d2，d3，…，dn,則：

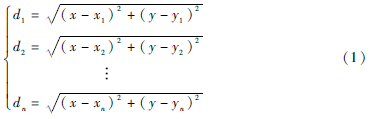
　　將式（1）轉化為線性方程AX=B形式，有以下關系：

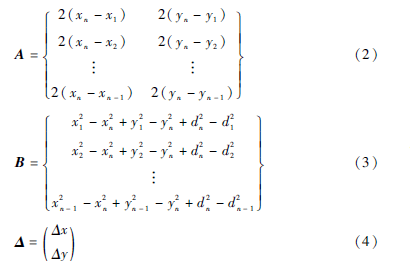
　　根據標準最小平均方差計算節點M坐標為:

　　X=(AT×A)-1×AT×B(5)

　　在上述定位過程中，極大似然估計算法通過周圍節點概率統計分布估算節點M位置。本文利用該思想建立移動節點信號漸變衰減模型，將周圍移動節點向量狀態轉換為對目的節點M的RSSI指紋參量的影響概率。

2新算法定位過程

　　2.1漸變模型

　　移動節點速率對周圍信號波動和多普勒頻移影響是一個漸變的過程［9］。各個節點信號參量以某種概率影響節點M的RSSI指紋參量。在漸變衰減模型中，距離d處信號強度是載波頻率、節點移動速率、影響概率和衰減因子構成的復雜函數，表示為：

　　RSSI(dBm)=RSSI(d0)－10×n×lg10(ddf)+Q×v×∑Pn(6)

　　其中，RSSI(dBm)是節點接收信號參量，f為信號頻率，d是實際距離，v為節點移動速率，Pn是來自移動節點n的影響概率，Q是修正參數。

　　2.2算法設計

　　泰勒級數是一種遞歸調用算法。由于移動節點速率對周圍信號的影響是一個漸變過程，節點速率越大，對RSSI測量誤差影響越大。新算法利用RSSI指紋參數值計算的距離信息和實際距離偏差遞歸校正概率影響參數Q,直到誤差小于一定范圍,結束遞歸調用，算法收斂。

　　設M為目的節點,測得其到周圍錨節點參考距離為d1,d2,d3,…,dk，速率為v1,v2,v3,…,vk，利用極大似然估計法計算M(x,y)作為初始位置，fi(x,y)表示目的節點M到周圍錨節點實際距離di之間的距離差值：

　　fi(x,y)=di－(xi－xd)2+(yi－yd)2－vi×t(i=1,2,3，…，n)（7）

　　將式（7）中距離節點M的初始距離M(xd,yd)和初始速率V(xv,yv)利用泰勒級數展開。為減少算法復雜性并計算影響概率Pn值, 舍去展開式高次項,得到式（8）:

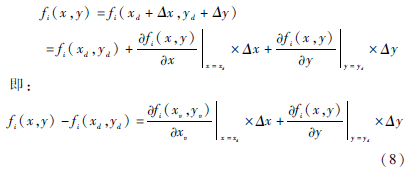
　　將式（8）轉換為矩陣運算形式A*Δ=B，其中：

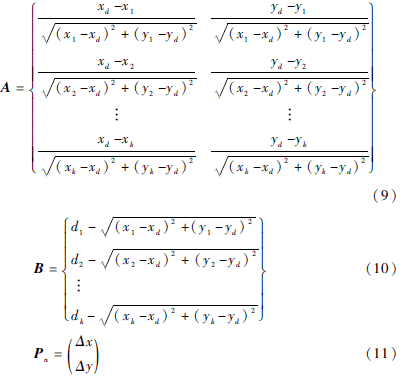
　　考慮節點移動速率對Pn的非線性影響，需施加權重因子Q并對A×Δ=B做加權矩陣修正。當加權矩陣Q為正定對角矩陣時：

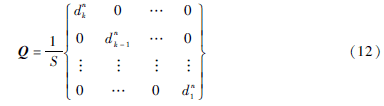
　　求線性方程A×Δ=Q×B的解：Δ=A－1×Q×B。

　　令:

　　xd=xd+Δx

　　yd=yd+Δy(13)

　　重復上述泰勒級數迭代過程, 直到|Δx|+|Δy|<ε,ε是偏差閾值，當校正量在閾值范圍內結束迭代，計算修正參數Q。

　　2.3誤差分析

　　假設目的節點M和錨節點i、n的實際距離分別為di^和dn^，估算距離分別為di和dn，則：

　　di^=di+di

　　dn^=dn+dn(14)

　　將n分別代入n和n-1項，計算n-（n-1）項有：

　　(di^)2－(dn^)=(di+di)2－(dn+dn)2(15)

　　得出目的節點M的平均定位誤差為：

3仿真測試

　　3.1測試環境

　　將節點隨機分布在100 m×100 m的網絡區域，設最大錨節點數量為90，隨機初始化節點移動狀態并限制v0∈［0,5］,節點通信半徑為20 m，利用MATLAB7.0軟件對算法進行仿真比較。

　　3.2靜態節點定位偏差測試

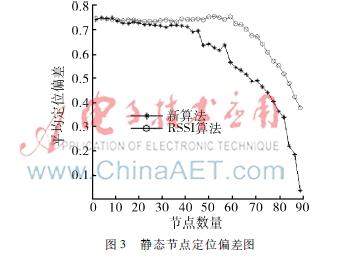
　　圖3靜態節點定位偏差圖當節點速率為0時，兩種算法定位偏差差別不大，在錨節點數量少于30個時兩條曲線幾乎重疊，如圖3所示。這是由于節點數量較小，泰勒級數修正值幾乎可以忽略不計。當節點數量大于60時，兩種算法定位偏差急劇下降，算法差異明顯。這是由于靜止節點之間雖然不存在信號多普勒頻移現象，但之間的信號波動和多徑衰減影響依然存在，此時泰勒級數修正可以很好地彌補RSSI易受環境干擾的不足，對移動節點定位更加精確。

　　3.3動態節點定位偏差測試

　　動態節點定位偏差測試結果如圖4所示。由于新算法考慮到節點移動因素，利用泰勒級數修正節點運動對周圍信號波動和多普勒頻移的影響，其平均定位偏差比傳統最大似然估計算法低約18.6%。另外，兩種算法偏差都隨節點密度的提高而逐漸減小，滿足無線傳感網絡定位的共性，但新算法更具優勢。

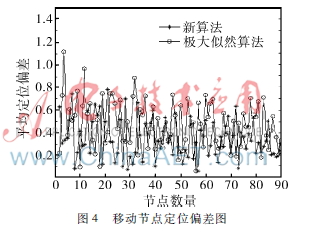
4結論

　　移動節點速率對周圍信號波動和多普勒頻移影響是一個漸變的過程，本文提出一種基于移動節點信號衰減漸變模型，利用極大似然估計算法思想將移動節點對周圍RSSI指紋參量影響轉變為概率事件，并通過泰勒級數修正漸變模型，減少節點移動對周圍電磁環境的影響，有效彌補了RSSI易受環境干擾的不足。算法相對復雜，但定位結果更為精確。

　　參考文獻

　　［1］ 曹曉梅,何欣,陳貴海.傳感器節點定位系統攻防機制研究［J］.計算機科學，2008,35(7):3641.

　　［2］ 鄧文蓮.無線傳感器網絡節點定位的仿真研究［J］.計算機仿真,2012,29(5):167169.

　　［3］ 梅舉,陳滌,辛玲.基于蒙特卡洛方法的移動傳感網節點定位優化算法［J］.傳感技術學報, 2013,26(5):689694.

　　［4］ 李鋒.粒子群離散算法在無線傳感網絡中的應用［J］.微型機與應用,2014,33(12):5456,60.

　　［5］ 石琴琴,霍宏,方濤,等.使用最速下降算法提高極大似然估計算法的節點定位精度［J］. 計算機應用研究,2008,25(7):20382042.

　　［6］ 陳三風,陳萬明.基于RSSI誤差分析的無線傳感器網絡定位研究［J］.計算機工程與應用, 2011,47(14):1012.

　　［7］ 沈軍,黃春華,羅護,等.基于RSSI優化的模型參數實時估計定位算法［J］.計算機工程與設計,2012,33(2):464468.

　　［8］ LAZOS L,POOVENDRAN R.HiRLoc:highresolution robust localization for wireless sensor networks［J］.IEEE Journal on Selected Areas in Communications,2006,24(2):233246.