吳宇翔,龔濤,梁文宇
(東華大學 信息科學與技術學院,上海 201600)
摘要:傳統模糊C-均值聚類算法需要輸入初始聚類中心,但是輸入錯誤的初始聚類中心會產生較差的圖像分割結果。對此提出一種改進的醫學圖像分割算法——基于免疫模糊聚類的醫學圖像分割。該算法能夠快速有效地找出合適的初始聚類中心值,使之最大可能地趨近于理想值,從而大大提高算法的效率,避免陷入局部解。同時,將免疫克隆選擇算法融入到模糊聚類算法中。實驗結果表明,該算法能快速有效地找到合適的初始聚類中心,能有效提高搜索效率和準確率,得到較理想的分割效果。
關鍵詞:免疫模糊聚類;圖像分割;克隆選擇
0引言
醫學圖像分割是醫學圖像處理的重要手段,圖像分割的優良會直接影響醫生對病情的診斷,所以醫學圖像分割一直是熱點問題。對于一般對比度明顯的圖片,直接利用簡單閾值算法進行分割即可,但是對于醫學圖像,灰度差異不明顯,圖像呈現模糊性。模糊聚類算法可以有效解決模糊圖像分割的問題。
模糊C-均值聚類算法目前應用已相當廣泛[1],如果初始聚類中心選擇不恰當,容易造成算法收斂到局部極值,會對結果產生較大影響,造成圖像誤分割。本文提出一種針對初始聚類中心改進的免疫模糊聚類算法(FCMAIA)。運用輪盤賭的思想產生接近目標函數極值的初始聚類中心,之后加入免疫克隆算法提高算法的搜索能力,以防止算法早熟,陷入局部解。
1模糊C-均值聚類算法(FCM)
聚類算法中,目前FCM算法是一種主流的迭代聚類算法[2],基于其模糊性的處理優勢,對醫學模糊圖像處理效果較佳。FCM算法分為以下幾步:待求解樣本數據集合R={r1,r2,r3,…,rn},根據先驗知識將樣本數據集合R中的數據分成c組,聚類中心V={v1,v2,…,vn},模糊隸屬度矩陣U={uij|i=1,2…,n,j=1,2,…,c},uij表示第i個樣本屬于第j個聚類中心的隸屬度,通過反復循環迭代調整V和U的值,使得目標函數J值最小,其目標函數定義為:

在滿足∑ci=1uij=1的條件下,根據拉格朗日乘數法,可得目標函數式(1)取得極小值的必要條件:
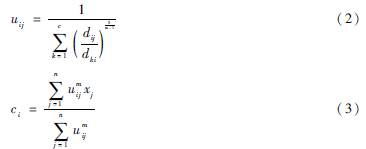
其中,m為權重系數,一般取值范圍是[1.5,2.5],本文令m=2;dij=xi-vj表示樣本點xi到聚類中心vj的歐式距離。
2基于人工免疫的模糊聚類算法
免疫系統具有無監督學習和自適應性的特性[3]。將人工免疫算法融入模糊聚類算法中,可以加強全局搜索能力,使解不易陷入局部峰值。相關概念定義如下:
圖1算法流程
(1)抗原:灰度圖像數據;
(2)抗體:聚類中心;
(3)抗體的產生過程:圖像數據的歸類過程。
算法流程圖如圖1所示。

2.1免疫模糊聚類迭代過程
算法流程如下。
(1)初始化聚類數目c,聚類中心V1(1),隸屬度矩陣U(1);
(2)在迭代過程中不斷修正聚類中心,將待求解存入記憶抗體庫;
(3)對記憶抗體庫中的抗體根據親和度大小進行克隆操作;
(4)將克隆抗體庫中的抗體按照親和力大小進行不等步長的變異;
(5)對更新后的記憶抗體庫根據抗體之間的親和度進行相應抑制操作;
(6)對隸屬度矩陣U不斷進行調整;
(7)計算免疫模糊聚類迭代當前代的親和度f,如果與前一代親和度相差結果小于某個閾值ε則迭代結束,否則轉至步驟(2)循環。
2.2初始化聚類中心計算
由于醫學圖像模糊性的特點,如果初始聚類中心選擇得不恰當,容易導致圖像分割效果較差。本文初始聚類中心查找過程如下:
(1)做出肺部圖像灰度直方圖,令直方圖中的最高點所對應的灰度值作為第一個聚類中心,如果出現多個相等峰值,隨機選擇其中一個即可;
(2)計算數據集中的樣本點r離最近聚類中心的距離L(r);
(3)選擇L(r)較大的點作為下一個聚類中心;
(4)不斷重復步驟(2)和步驟(3)直到找出所需初始聚類中心個數。
其中關鍵步驟是步驟(3)中D(X)能夠反映被選取點的概率,算法實現過程如下(類似輪盤賭原理):
①對于每個點,計算其與最近的一個聚類中心的距離D(X);
②將所有D(X)相加,得到Sum(D(X))+=D(X);
③取一個[0,1]之間的隨機值random(n),令S=random(n)*Sum(D(x));
④利用S-=D(X),直到S<0,此時對應的點就是下一個初始聚類中心。
2.3親和度計算
基于免疫計算的圖像聚類算法[4],通過不斷優化隸屬度U和聚類中心V,使圖像數據達到較理想的聚類效果,本文采用基于誤差平方和準則定義抗體親和度f。
親和度f的公式定義如下:

從式(4)可以看出,目標函數J值越小,親和度越大,圖像數據聚類分割效果越好。如式(5)所示。

2.4記憶抗體克隆選擇操作
本文中記憶抗體庫存儲待求解聚類中心,為使結果不陷入局部最優解,加速全局搜索能力,需要對記憶抗體庫抗體進行比例不一的克隆選擇操作[5]。抗體克隆個數由式(6)確定:
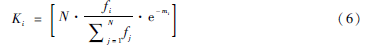
其中,fi表示第i個抗體的親和度值,N表示抗體總數,mi表示相似抗體濃度因子。
相似抗體過多會導致克隆抗體庫的抗體趨向均等化,不利于增加抗體的多樣性。針對此問題,本文加入可調節相似濃度因子。設定閾值δ,當抗體之間親和度差值小于該值時,稱為相似抗體。抗體i的相似抗體因子mi=p·NiN。其中,p為調節系數,Ni為相似抗體數。
2.5克隆抗體庫選擇性高頻變異
本文根據抗體親和度大小相應地采用小步長和大步長相結合的變異過程。對親和度高的抗體采用小步長的高斯變異,提高局部搜索能力,不斷提高解的精度。對親和度低的抗體采用大步長的柯西變異,使親和度低的抗體向優良抗體靠攏。
(1)高斯變異——小步長變異

其中,gi表示第i代抗體,g′i為變異后的抗體,N(0,1)為均值μ=0、方差σ=1的隨機高斯分布,β是控制函數衰減的因子,f為親和度。
(2)柯西變異——大步長變異
g′i=gi+α·φm(9)
其中,φm為柯西方程產生的隨機概率數,α為修正步長參數。
經過記憶抗體克隆選擇操作和克隆抗體庫選擇性高頻變異之后,通過將變異后的抗體進行排序,選擇克隆抗體庫中親和度高的一部分抗體替換記憶抗體庫中親和度較低的抗體,完成記憶抗體庫更新操作。
2.6記憶抗體庫免疫抑制操作過程
在記憶抗體庫不斷迭代的過程中,需要對抗體作免疫抑制操作[6],避免抗體集中分布,防止記憶抗體庫抗體趨于無差別化。在此,定義抗體之間的親和度為:

其中,dij=xi-xj為第i個抗體與第j個抗體之間的歐式距離,歐氏距離越小,表明抗體之間的親和度越高,就越需要抑制操作,保持記憶抗體庫多樣性;反之,則保留。
免疫抑制過程如下:
(1)根據歐式距離公式得出記憶抗體庫中任意兩個抗體之間的距離,根據式(10),得出fij;
(2)設定閾值τ,當任意抗體對親和度fij>τ時,隨機刪除其中一個抗體并隨機從克隆抗體庫篩選一個抗體補充記憶抗體庫。
3實驗與分析
本文所用算法均在MATLAB 2010a環境進行。為了驗證新算法的有效性,準備一張肺部原始圖像,圖像大小為225×224,圖像整體偏暗,對比度較低,邊界較模糊,如圖1所示。將本文算法應用于該肺部圖像分割中,為了進行對比,將普通C均值聚類算法與經典遺傳算法進行比較,比較內容分為圖像質量和分割效率。在免疫模糊聚類分割中,設置c=2,最大迭代次數n=50。
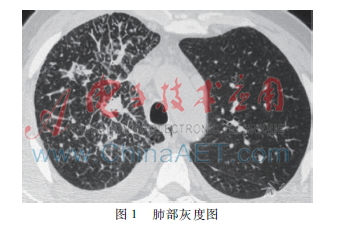
表1列出本文算法與普通C均值聚類算法分別應用于上述肺部圖片得到最佳閾值對和所消耗時間。由表可看出,本文算法搜索到最佳閾值對的時間相對普通C均值聚類算法時間效率大大提高,主要是因為利用本文算法可以有效地選取接近最佳閾值對的聚類中心,并加入克隆選擇,通過抗體克隆、變異,選擇加速全局收斂。可以看出,本文算法用于醫學圖像處理可行。

表2給出本文算法與經典遺傳算法對肺部圖像分割結果迭代次數的比較,本文算法迭代10次可以得到最優聚類中心,但是經典遺傳算法在10次迭代以內無法搜尋 到最優值,經過20~30次迭代,搜索能力才有所加強,勉強找到最優值。本文算法中的克隆選擇過程通過克隆選擇、變異、免疫抑制確保優秀抗體可以得到保存,從而加速收斂效果。
本文算法與C均值聚類算法和經典遺傳算法的圖像分割結果如圖2所示。

4結論
本文提出一種基于改進的免疫模糊聚類算法,通過算法初步得出最佳的初始聚類中心,防止其落入局部極值附近,加速搜索速度。在此基礎上加入免疫克隆算法,保證抗體的多樣性和全局尋優能力。實驗證明,肺部圖像分割較清晰,有助于醫生對肺部疾病的判斷。后期改進工作中,需要不斷提高算法精度,使其達到醫學圖像的精準分割,真正適用于臨床醫學研究。
參考文獻
[1] 高洪波.模糊聚類分析及其應用[M].西安:西安電子科技大學出版社,2004.
[2] BEZDEK J C, PAL S K. Fuzzy models for pattern recognition[M]. Piscataway, New Jersey: IEEE Press, 1999.
[3] 葛紅.免疫算法綜述[J].華南師范大學學報(自然科學版),2002 (3):120126.
[4] 王磊,潘進,焦李成.免疫規劃[J].計算機學報,2000,23(8):806812.
[5] 肖人彬,王磊.人工免疫系統:原理、模型 、分析及展望[J].計算機報,2002,25(12):12811293.
[6] 劉麗玨,唐琎,蔡自興.一種用于函數優化的免疫算法[J].電子技術應用,2006,32(6):2224.

