張檣,周西峰,郭前崗
(南京郵電大學 自動化學院, 江蘇 南京 210046)
摘要:利用最小二乘法將超聲回波參數估計問題轉化為優化問題,采用改進的差分進化算法(DE算法)對待優化函數進行優化處理。仿真研究說明,該方法在噪聲環境下依然有效,并且不依賴于初始值選擇,不需計算梯度,可以在全局范圍內搜索。
0引言
超聲無損檢測一直是無損檢測的研究熱點,超聲信號波形中包含有被檢測物體的幾何形狀、大小、缺陷故障等一系列有價值的信息。模型化的超聲信號分析方法能有效提取信號中有用信息,其中每個回波模型都是一個非線性函數包含有一系列的參數:回波帶寬、中心頻率、相位、幅度、超聲回波的渡越時間。這些參數實時反映超聲信號的波形,并且與反射器的物理特性以及傳播路徑的頻率特性密切相關[1]。1981年,SANIIE J[2]提出了利用高斯回波模型模擬超聲信號的方法; 2001年,DEMIRLI R[3]利用高斯牛頓算法迭代出了高斯回波模型的參數,具有十分高的精度。但是高斯牛頓法過度依賴于初值點的選取,若初值點選取偏差較大將會影響算法整體的收斂性,而且該算法從理論上來說獲取的是局部最優解,并非全局最優解,所以這種方法在實際應用中具有很大局限性。
針對以上問題,本文基于超聲回波信號的高斯模型,提出改進的差分進化算法對超聲信號的參數進行估計。
1差分進化算法原理
差分進化算法是基于群體智能理論的優化算法[46]。按照算法分析指標對DE算法分析如下:(1)在編碼標準方面,DE算法與粒子群優化算法類似,都是采用實數編碼;(2)在參數設置問題上,研究表明DE算法的參數設置較少,對結果影響不是很明顯,優于遺傳算法和粒子群優化算法;(3)在高維問題中,DE算法和粒子群優化算法能夠很好地解決問題,而且DE算法收斂快且精確;(4)收斂性能上,粒子群優化算法容易陷入局部最優解并且不穩定,DE算法不存在這樣的問題。差分進化算法的基本原理是:采用對個體進行方向擾動,以達到個體的函數值下降的目的。同其他進化算法一樣,差分進化算法不利用函數的梯度信息,因此對函數的可導性甚至連續性沒有要求,適用性很強。DE 算法的搜索性能取決于算法全局探索和局部開發能力的平衡 ,而這在很大程度上依賴于算法的控制參數的選取 ,包括種群規模、縮放比例因子和交叉概率等[7]。但是實驗表明,在噪聲環境下差分進化算法的優化功能遠遠低于進化算法。本文所應用的改進差分進化算法能有效處理噪聲環境下函數優化。
2超聲回波模型
超聲換能器的脈沖響應可以模擬成高斯信號[8],響應的脈沖幅度可以表示為:
x(t)=βe-αt2cos(2πfct)(1)
高斯回波的一般模型為:
s(θ;t)=βe-α(t-τ)2cos[2πfc(t-τ)+](2)
參數向量θ=[βατfc]為超聲回波的參數向量。其中,α為帶寬,τ為到達時間,fc為中心頻率,為相位,β為幅度系數。
回波模型做加性白噪聲處理得到:
y(t)=s(θ;t)+v(t)(3)
其中,v(t)為加性高斯白噪聲。
3改進差分進化函數算法
為了準確估計超聲信號模型參數,首先應用最小二乘法構造目標待優化函數[9]如下:
J(θ)=[y-s(θ)]T[y-s(θ)]=y-s(θ)2(4)
問題就轉化為求J(θ)為最小值時的參數向量θ,J(θ)為目標待優化函數,y為實際信號,s(θ)為信號模型,θ為目標待估測參數向量。
4改進差分進化算法
差分進化算法的參數定義[1011]如下:
NP:群體大小,即種群中個體數目,NP越大,種群多樣性越強,活動最優解的概率越大,但是計算量也越大,一般選擇在5D~10D之間;
F:變異因子,經典DE算法中它是一個實常數因數,圖1超聲估計信號它決定偏差向量的放大比例,本文方法中將F定義如下:
F=0.5×(1+rand(0,1))(5)
比列因子的均值保持在0.75,因子的隨機變化有利于搜索的多樣性,在真正的最優解搜索到之前不易陷入停滯,在噪聲背景下,尤其適用。
CR:交叉因子,經典DE算法中它是一個范圍在[0,1]的實數,控制一個試驗向量來自隨機選擇的變異向量而不是原來向量的概率的參數。
G:最大迭代次數,G越大,獲得的最優解越精確,計算量增加;
D:問題維數;
Xi(t):群體中每個目標個體;
Vi(t):變異的目標個體;
Ui(t):交叉操作后的試驗個體。
算法具體步驟如下:
(1)初始化種群,同時初始化算法中的各參數;
(2)計算每個個體的適應值,適應度函數根據具體問題決定;
(3)判斷是否滿足終止條件(終止條件是指找到最優解或者達到最大迭代次數),若是則進化終止得到最優解,若不滿足終止條件則跳到步驟(4);
(4)執行變異操作,將式(5)代入式(6)中:
Vi(t)=Xr1(t)+F×(Xr2(t)-Xr3(t))(6)
產生變異個體Vi(t),其中i、r1、r2、r3是取值在1~NP之間的4個不同整數,執行步驟(5);
(5)執行交叉操作,按照式(7)生成試驗個體Ui(t);
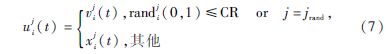
(6)執行選擇操作,采用的是貪婪選擇的策略,即選擇較優的個體作為新的個體:
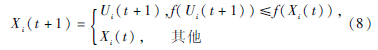
f(*)即目標待優化函數J(θ)。
5仿真結果與分析
在仿真試驗中,超聲信號的模型參數向量取值為θ=[3.2253.551.8]。超聲信號的采樣頻率為100 MHz,采樣信號保存為s(θ),分別在該信號中添加30 dB、20 dB、10 dB的高斯白噪聲作為實測信號。估計出的信號如圖1所示。

在差分進化算法中設置種群NP=50,交叉因子CR=0.3,最大迭代次數為500,仿真結果如表1所示。
從表1可以看出,無噪聲情況下高斯法可以100%的估計得到原始信號,本文方法有誤差,但是與真實值很接近,如圖1(a)所示。在有噪聲信號的影響下,高斯法根本無法迭代估計參數,本文方法可以得到優化解。但是隨著噪聲影響增大,估測得到參數的誤差也在加大,但是超聲信號特征參數的3個重要參數估測的精確度依然很高,誤差分析如表2所示。

6結論
本文提出利用最小二乘法構造目標待優化函數,并應用DE算法的變異因子的特點提出改進的DE算法估計噪聲情況下的參數,該方法充分利用DE算法對初值依賴性不大、不需計算梯度、善于在全局范圍內搜索等優點。實驗結果表明,與高斯牛頓法相比,該算法收斂速度很快而且結果很精確,具有很高的工程應用性。
參考文獻
[1] DEMIRLI R. Model based estimation of ultrasonic echoes: analysis, algorithms, and applications[M]. Illinois Institute of Technology, 2001.
[2] SANIIE J. Ultrasonic signal processing: system identification and parameter estimation of reverberant and inhomogeneous targets[J]. Ultrasonic Signal Processing: System Identification and Parameter EST, 1981.
[3] DEMIRLI R,SANIIE J.Modelbased estimation of ultrasonic echoes. Part I: analysis and algorithms[J]. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 2001,48(3):787802.
[4] Fan Huiyuan, LAMPINEN J. A trigonometric mutation operation to differential evolution[J]. Journal of Global Optimization, 2003, 27(1): 105129.
[5] 胡中波.差分演化算法及其在函數優化中的應用研究[D]. 武漢:武漢理工大學,2006.
[6] 李凱斌.智能進化優化算法的研究與應用[D]. 杭州:浙江大學,2008.
[7] KRINK T, FILIPIC B, FOGEL G B, et al. Noisy optimization problemsa particular challenge for differential evolution[C].Proceedings of the 2004 Congress on Evolutionary Computation,2004:332339.
[8] 周方,張小鳳,張光斌.超聲回波參數的蟻群算法估計[J]. 陜西師范大學學報(自然科學版), 2012,40(2):3540.
[9] 周西峰, 朱文文, 郭前崗. 基于遺傳算法和高斯牛頓法的超聲回波信號參數估計[J]. 解放軍理工大學學報(自然科學版), 2012, 13(3): 247251.
[10] 汪艷, 張小鳳, 張光斌, 等. 基于高斯模型的多重超聲回波信號重數估計[J]. 陜西師范大學學報 (自然科學版), 2015,43(1):7.
[11] 潘欣,高曉智.基于差分演化的果蠅優化算法[J].微型機與應用,2015,34(1):2325,28.

