郭鵬杰1,2,唐莉萍1,2
(1.東華大學 信息科學與技術學院,上海 201620;2.東華大學 數字化紡織服裝技術教育部工程研究中心,上海 201620)
摘要:討論了一種通過地磁進行智能系統導航控制的方法,通過地磁傳感器獲得智能系統的行駛狀態,并對地磁導航角進行誤差校正。綜合考慮車輛速度、轉向角大小等因素對智能系統行駛狀態的影響,提出一種適用于內核為Cortex_M4的智能小車轉向控制策略。
關鍵詞:地磁導航;智能系統;行駛狀態;轉向控制
0引言
21世紀,智能交通系統的飛速發展引發了智能導航技術的不斷進步。機器視覺由于其具有檢測范圍廣、信息容量大、類似于人類駕駛決策且成本低廉等諸多優勢,在國內外智能導航的研究中得到了廣泛應用[1]。但是機器視覺是通過視覺識別道路和障礙物,進而規劃路徑實現導航控制,控制結果容易受天氣狀況、光照等因素影響。全球定位系統(Global Positioning System,GPS)是另一種廣泛應用的導航技術,它可以為全球用戶提供三維位置、速度等信息[2]。但是GPS導航具有一定的局限性,它在使用時要求用戶實時連接網絡或者存儲高精度的數字地圖,否則其導航精度和實時性難以保證[3]。
地磁場是地球的固有資源,它能為航天、航海、航空提供天然的坐標系[3,4]。由于地磁場的矢量性,通過地磁傳感器感知測量即可確定系統當前的運動狀態信息[5,6]。與其他導航方式相比,地磁導航具有無源、全天候、全地域、低能耗等優勢,在工業部門、航空航天等諸多領域發揮了重要作用,成為近年來智能導航學術界關注的對象[7]。
本文在參考文獻[812]的基礎上,對基于地磁傳感器自動導航的智能小車控制方法進行探討,結合系統硬件框圖,對基于地磁導航的控制策略進行研究,并采用PID控制導航。對通過地磁傳感器獲得的當前航向角度,判斷其與目標角度的夾角的偏差,給出轉向角度指令,調節舵機,實現小車自動路徑行駛。最后在研究的理論算法基礎上,考慮硬件平臺限制,給出優化方案,并通過實踐證明該優化方案的可行性。
1系統設計總體方案
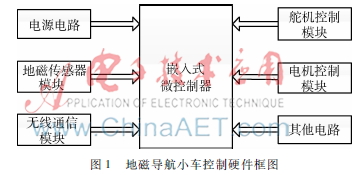
地磁導航小車在自動路徑運動中不斷通過地磁傳感器獲得當前行進方向的角度信息,與預設路徑的航向角比較,通過所得結果的偏差角度調整舵機的偏轉方向,從而控制智能小車的行駛軌跡。系統的硬件主要模塊如圖1所示。其中地磁傳感器采用意法半導體公司的MEMS數字集成芯片LSM303DLHC。
2地磁導航角度計算
圖5系統控制流程地磁傳感器只能提供當前所在區域的磁場量,要獲取當前小車的導航角,必須計算地球磁場和導航角之間的關系并進行標定。

地球的磁場總是由地磁南極指向地磁北極,在極點處磁場與當地水平面垂直,在赤道處與當地水平面平行,如圖2所示。對于地球上絕大部分區域來說,當地地磁場均可視為與水平面平行。由于地磁場是一個矢量,任意一點的地磁場都可以分解為兩個平行于當地水平面的分量和一個垂直于當地水平面的分量。如果保持地磁傳感器和當地的水平面平行,那么就有圖3所示的地磁傳感器的3個軸和這3個分量對應關系。
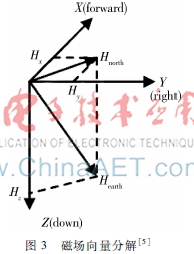
圖3磁場向量分解[5]圖3中,Hnorth和Hz分別為Hearth在水平面和垂直面的分量,Hx和Hy為Hnorth在相對坐標系X軸和Y軸的分量。
在水平方向上磁場兩個分量的矢量和總是指向磁北。地磁傳感器中的航向角(Azimuth)是當前方向和磁北的夾角,即:

當地磁傳感器保持水平,航向角只需要用傳感器水平方向兩軸(通常為X軸和Y軸)的數據就可以由式(1)計算得到。當地磁傳感器水平旋轉時,航向角在0°~360°之間變化。如果設備不是水平放置,那么設備與水平面存在一個夾角θ,如圖4所示。這個夾角將影響航向角的計算精度,需要借助加速度傳感器進行傾角補償。先通過測量3個軸上重力加速度的分量,得到:
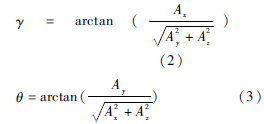
再將地磁傳感器測的得數據(XM,YM,ZM)通過γ和θ轉化為Hx、Hy:
Hy=YMcos(θ)+XMsin(θ)sin(φ)-ZMcos(φ)sin(θ)(4)
Hx=XMcos(φ)+ZMsin(φ)(5)
結合式(1)即可計算出航向角ψ。
圖4設備與水平面之間存在夾角[5]

3基于地磁導航的控制策略
3.1智能系統控制模型
智能導航控制的實質是對小車前進方向角度與設定目標角度偏差的控制。主要控制算法是基于自適應的PID控制。系統控制流程圖如圖5所示。
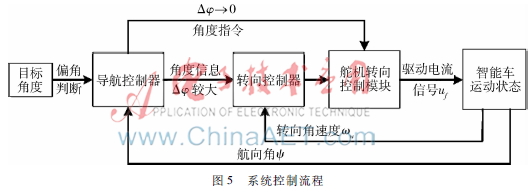
導航控制的具體過程如下:導航控制器根據接收到的智能車運行航向角信息ψ與設定目標角度進行比較,計算出航向偏差Δφ。當Δφ較大時,轉向控制器通過收到的角度信息和反饋的角速度信息計算出合適的轉向角θ,系統經過大角度轉向、預判目標、回轉等一系列操作后,以較小的偏差角度切入目標航線;當Δφ→0時,直接經過PID控制算法生成角度控制指令u,然后通過導航控制器不斷調整,系統進入直線行駛控制狀態。
3.2轉向控制器設計
轉向控制器采用PID控制方法,設定量和控制量都是角度值,反饋量為智能系統的轉向角速度ωw。
本地磁導航系統以方向角為預瞄條件,其中車輛系統的二自由度運動模型如圖6所示。
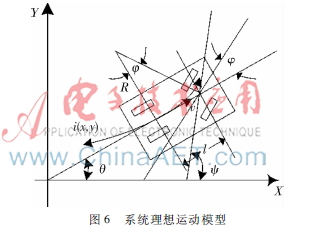
圖6中,θ為智能系統相對于相對坐標系x軸的方向角;φ為舵機轉角;R為智能系統的轉彎半徑;l為車輛軸距;v和ω分別為智能系統在點(x,y)處的速度和前輪轉向角速度。由圖6所示的車輛運動幾何關系可以得到車輛的運動模型如下:

為了使軌道誤差最小,根據智能系統當前狀態下的理想側向速率(t)與理想側向加速度(t),由系統理想運動模型,此時智能車所需理想側向加速度為:
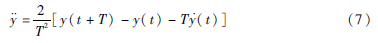
同時,在不考慮車輛的滯后情況下,其運動簡單地服從Acklman幾何關系。

式(8)表明智能車的曲率1/R與方向盤轉角δ成正比,即智能車轉彎半徑R與方向盤轉角δ成反比。汽車的側向加速度同時與車速v和舵機轉角φ有關。智能車通常行駛在低速狀態下,系統通過調整轉向角度即可獲得良好的轉彎半徑。考慮到切入目標角度和轉彎半徑的約束,必須首先輸出一個較大的轉向角度,然后達到此角度后舵機進行回轉,以達到切入目標角度時角度偏差最小的目的。
由于轉向系統中方向偏角是不斷積累的過程,故PID控制器采用比例控制和積分控制就能實現控制目的。這里采用位置式PID算法。
uf(k)=uf(k-1)+Kp[δe(k)-δe(k-1)]
+KiTδe(k-1)(9)
其中,uf為控制信號量,T為系統采樣周期,δe(k)為角度偏差,Kp為比例系數,Ki為積分系數。
3.3導航控制器設計
導航控制器采用PID控制算法,設定值為目標角度,反饋量為當前航向角ψ;當系統直線行駛或者與目標角度的偏差較小時,系統進入直行導航階段。為了防止系統調節時出現振蕩現象,當地磁傳感器所得到航向角與目標角度的偏差在±2°以內時,系統不進行調整,運動方向不發生改變。當偏差達到±3°時,系統采用PID控制方法調整智能車方向。
為了提高系統響應速度,算法采用比例控制方法,控制率為:
δ=αθ(10)
其中,δ代表轉向角指令,α為比例系數。
4實驗結果與改進
本文設計的智能小車其核心是Cortex_M4,嵌入式設備由于硬件限制,其運算能力不及PC,如果按照常規的控制算法進行自動導航,系統必然出現較大延時;如果要提高系統響應速度,則會影響系統轉向角的控制精度。因此需要對第3節討論的方法進行改進,以期在時間和精度之間得到一個較優的平衡。在智能小車自動導航過程中,可以將目標角度進行區域劃分,針對不同的車速和角度區域,根據經驗值設置不同的轉角指令,將智能車的轉彎曲線軌跡盡可能擬合為理想轉彎軌跡,以達到良好的轉彎效果。
在圖4所示的理想運動系統模型中,Δφ是系統導航控制的關鍵因素。在自動導航實驗中, 取Δφ≤2°角度作為導航控制器判斷的閾值時,系統具有良好的響應速度,但是系統偏角響應處理很快,系統振蕩周期較短,以至于系統出現明顯的左右擺動。取Δφ>5°時,系統有明顯的響應延時,造成明顯的路徑偏移。根據實驗結果取Δφ=±3°作為導航控制器和轉向控制器的閾值。
PID參數的選擇是影響系統性能的重要因素,對PID參數的整定比較繁瑣,需要進行復雜的積分、微分計算。這些運算如果在嵌入式硬件平臺上實現,由于計算工作需要占用大量的時間,系統的實時控制能力將下降。為此,對PID參數可以采用查表法進行選擇。首先建立一個模擬系統,計算出系統在不同角度與不同車速下的PID參數,再通過實驗不斷調整優化,最終建立PID參數經驗表。
優化過后的系統導航控制過程如圖7所示。

導航控制流程如下:MCU通過地磁傳感器獲得數據并計算出當前行駛角度v以及與目標角度的偏角差值Δφ,通過查找經驗表獲得適合當前車速與偏角Δφ的PID控制系數,然后調節PWM的占空比調節舵機轉向角度大小。
5結論
實踐證明:通過經驗表代替系統復雜的積分微分運算,在幾乎不影響系統的運行穩定性的情況下,提高了系統的響應速度,此優化方案具有可行性。
參考文獻
[1] 郭才發,胡正東,張士峰,等.地磁導航綜述[J].宇航學報,2009, 30(4): 1314-1319.
[2] 尤亞男.智能車輛導航技術[J].金田,2013(8): 346,323.
[3] STORMS W, SHOCKLEY J, RAQUET J. Magnetic field navigation in an indoor environment[C].Ubiquitous Positioning Indoor Navigation and Location Based Service (UPINLBS), 2010, IEEE, 2010: 1-10.
[4] 李興城,張慧心,張雙彪.地磁導航技術的發展現狀[J].飛航導彈,2013, 10(10): 80-83.
[5] 陳偉韜. 基于MEMS傳感器的電子羅盤系統的設計[D].廣州:廣東工業大學,

