摘要： 針對反射式太赫茲時域光譜系統所測時域信號存在反射峰、頻譜出現振蕩、頻域信噪比低等問題，提出基于經驗模態分解處理太赫茲時域反射峰的方法，同時消除頻域振蕩的影響。通過獲取本征模函數并代替反射峰，增加時域信號有效長度、提高太赫茲頻域分辨率，消除頻域振蕩影響。古代壁畫樣本的太赫茲反射譜實驗結果表明，該方法能自適應地處理反射峰，對太赫茲時域信號修復效果良好，頻域振蕩抑制效果良好。

　　關鍵詞：太赫茲反射譜；經驗模態分解；反射峰處理

0引言

　　太赫茲(THz)波是指頻率在03~3 THz范圍內的電磁波，對應的波長范圍為100 μm~1 mm［1］。由于太赫茲波有許多優越的特性，其在食品安全［2］、無損檢測［3］、生物分子探測［4］和毒品檢測［5］等方面都具有非常重要的科學價值。

　　太赫茲時域光譜（THzTDS）技術是20世紀80年代由IBM公司和AT&T Bell實驗室聯合發展起來的一種有效的相干探測技術［6］，該技術不僅能夠獲得THz脈沖的振幅，同時也能獲取相位信息。THzTDS系統主要有反射式THzTDS系統和透射式THzTDS系統，如果需要測量的樣品是較厚的介質或樣品吸收特別強，那么需要使用反射THzTDS系統來對其進行測量。因此，針對古代壁畫樣本，本文采用反射式THzTDS系統對樣品進行測量。

　　經驗模態分解(Empirical Mode Decomposition,EMD)是20世紀90年代后期由華裔美國院士黃鄂提出的自適應時頻分析方法［7］。相比于傳統的時域相關分析、時頻域小波變換等方法，EMD［8］在處理非平穩、非線性數據上具有明顯的優勢。

1算法原理

　　1.1EMD算法簡介

　　EMD的核心思想是能將復雜信號分解為若干個本征模函數(Intrinsic Mode Function，IMF)之和。 黃鄂認為，IMF分量必須滿足下面兩個條件：（1）在全部時間范圍內，局部極值點數和過零點數必須相等，或最多相差一個；（2）在任意時刻，局部最大值的包絡與局部最小值的包絡的平均值必須為零。本文利用EMD將復雜的原始信號分解成瞬時頻率不同的若干個IMF的特性去除THz反射峰。

　　1.2THz時域反射譜的EMD分解

　　下面采用EMD方法將復雜的原始測量信號分解成瞬時頻率不同的若干個IMF：

　　（1）找出原始測量信號中反射信號x(t)的所有局部最大值點和最小值點；

　　（2）分別得到(1)中的上包絡線xmax(t)和下包絡線xmin(t)：

　　xmin(t)≤x(t)≤xmax(t)(1)

　　（3）計算上包絡線和下包絡線的均值：

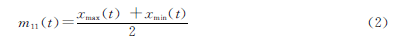
　　（4）得到x(t)去掉均值的新數據序列h11(t)：

　　（5）檢查h11(t)是否滿足本征模函數的條件，對于復雜信號，一般情況下，需要對h11(t)重復上述處理過程，直到滿足本征模函數的定義要求為止，則：

　　h1k(t)=h1(k-1)(t)-m1k(t)(4)

　　c1(t)=h1k(t)=x(t)-∑ki=1m1i(t)(5)

　　令：r1(t)=x(t)-c1(t)(6)

　　（6）以r1(t)為反射信號，重復上述處理步驟，則可以得到其他本征模函數：c2(t)、c3(t),...,cn(t)，即

　　cn(t)=rn-1(t)-rn(t)(7)

　　其中rn(t)稱為余項。至此，原始反射信號的EMD分解結束，原信號可以表示為：

　　x(t)=∑ni=1ci(t)+rn(t)(8)

　　分解出的本征模函數按頻率由高到低依次排列，本文選擇最后一個本征模函數，并用它替代原始的反射峰信號，獲得處理后的THz時域光譜信號。

　　2實驗結果與討論

　　采用12節的方法處理THz時域反射峰，然后通過快速傅里葉變換(FFT)得到時域反射峰被處理后的頻域譜。

　　圖1和圖2分別為參考和測量信號EMD處理前后THz時域反射譜對比圖。通過比較圖1、圖2可以明顯看出，兩個信號的反射峰的處理效果良好。

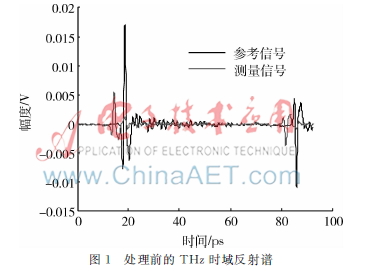
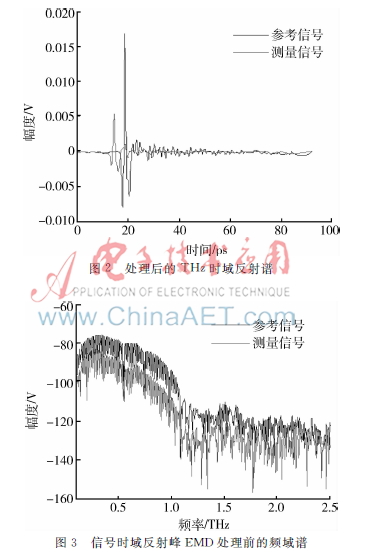
　　圖3和圖4分別為參考和測量信號EMD處理前后THz頻域反射譜對比圖。通過比較可以明顯地看出，參考信號和測量信號的時域反射峰被處理掉后，其頻域譜的振蕩被很好地抑制了，可以在頻率為015~11 THz范圍內觀察到很明顯的3條水的吸收峰，提高了頻域信噪比，更有利于研究樣本的吸收特性。

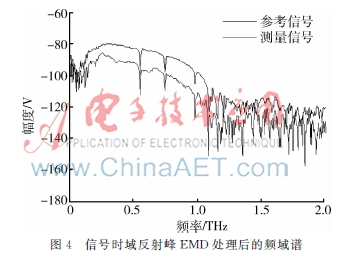
3結論

　　針對太赫茲反射譜中時域存在反射峰與頻域出現振蕩的問題，本文首次提出利用EMD自適應分解和處理THz時域反射峰的解決方法。以古代壁畫樣本的THz反射譜為例，比較了EMD處理時域反射峰前后的時域譜，反射峰消除效果良好；通過比較經EMD處理前后的頻域譜，發現頻域振蕩影響被很好地抑制，水的吸收峰明顯，提高了頻域信噪比，有利于進一步研究樣本的吸收特性。由于反射峰的去除可增加時域有效數據，因此也提高了頻率分辨率。

　　參考文獻

　　［1］ SIEGEL P H. Terahertz technology［J］. IEEE Transactions on Microwave Theory and Techniques, 2002, 50(3): 910928.

　　［2］ MASSAOUTI M, CHRISTINA D, GORODETSKY A, et al. Detection of harmful residues in honey using terahertz timedomain spectroscopy［J］.Applied Spectroscopy, 2013,67(11):12641269.

　　［3］STOIK C, BOHN M, BLACKSHIRE J. Nondestructive evaluation of aircraft composites using reflective terahertz time domain spectroscopy［J］. NDT&E International 43, 2010, 43(2):106-115.

　　［4］ VALERIA N C, MARTINA H. New insights into the role of water in biological function: studying solvated biomolecules using terahertz absorption spectroscopy in conjunction with molecular dynamics simulations ［J］. Journal of the American Chemical Society, 2014, 136(37): 1280012807.

　　［5］ He Ting, Shen Jingling. Applications of terahertz spectroscopy in illicit drugs detection ［J］. Spectroscopy and Spectral Analysis, 2013, 33(9):23482353.

　　［6］ 趙國忠. 太赫茲科學技術研究的新進展［J］. 國外電子測量技術,2014,33(2):16,20.

　　［7］ HUANG N E,Shen Zheng, STEVEN R L, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences . 1998,454:903995.

　　［8］ 寇艷廷,范濤濤,劉晨,等.EMD過程中數據擬合的算法改進與實現［J］.微型機與應用,2013,32(5):6668.