摘  要： 通過構建超聲回波信號模型，將基于小波包閾值去噪應用在超聲回波信號研究中。針對超聲回波信號的非平穩性，提出一種多閾值分段去噪方法應用于超聲回波信號的去噪研究中。仿真實驗表明，采用的多閾值分段去噪克服了單閾值規則的局限性，能夠較好地處理超聲信號中的噪聲分量。

　　關鍵詞： 超聲回波信號；小波包閾值去噪；非平穩性；多閾值

0 引言

　　超聲無損檢測技術是通過換能器發射脈沖與被檢測對象相互作用，并接收目標的反向散射回波來進行相關研究，達到對檢測對象進行宏觀缺陷、幾何特性、組織結構和力學性能等特定性評價的非侵入式檢測技術[1]。超聲檢測的回波信號是時頻有限的非平穩信號，需要表示局部時間范圍內的頻譜信息，傳統的頻域或時域分析方法不能滿足回波信號處理的要求。而小波變化由于具有靈活性、快速性、時頻雙域性等特點，成為分析非平穩信號的一種重要工具[2]。

　　小波去噪是小波變換在信號處理中的關鍵應用之一，主要方法有模極大值去噪、相關性去噪、小波閾值去噪等，其中小波閾值去噪因計算量較小，能保持信號奇異性被廣泛應用[3]。小波包閾值去噪在對信號低頻部分進行分解的同時，還能對信號的高頻部分進行分解，有效地提取各頻段的有用信息，更適合高精度的超聲回波信號分析[4]。目前傳統的幾種單閾值規則去噪方法因各自的局限性，無法在噪聲污染不穩定的各個頻段實現高精度去噪。為此提出一種多閾值分段去噪的方法，它克服了單閾值規則的局限性，仿真實驗結果也表明了這種去噪方法的可行性和優越性。

1 超聲傳播特性及回波信號模型

　　超聲檢測聲源一般由若干探頭晶片組成，發射的聲波形成一個沿著有限范圍向一定方向傳播的超聲束。超聲波在介質中傳播，并接收目標的反向散射回波，通過對獲得的目標回波進行分析，確定反射目標的物理特性和傳輸路徑上的各種信息。然而超聲波在傳播過程中由于受到聲束散射、介質吸收、異質界面的彈性反射以及外界加性噪聲的影響，所接收的回波信號會發生一些噪聲污染，因此精確的回波信號至關重要。經研究發現，超聲回波存在非線性現象，這種現象可用模型逼近。常用的超聲脈沖經驗模型有高斯脈沖模型、混合指數模型和雙指數模型，其參數設置靈活、估計精度高，被廣泛應用于模擬仿真中。

　　超聲換能器的脈沖響應可模擬成高斯信號，響應的脈沖幅度可表示為：

　　而底面回波、缺陷回波與材料散射波信號的產生機理十分相近，都是發射的超聲波入射到試件中遇到阻礙時，產生的波反射和散射信號。在寬帶窄脈沖超聲檢測中，根據超聲回波的物理特性，忽略在實際檢測中缺陷反射對超聲脈沖頻率的影響，用超聲換能器脈沖響應幅度的修改模型s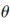（，t）表示接收到的有用回波信號[5]：

　　回波模型做加性噪聲處理可得含噪超聲回波模型：

　　x（t）=s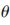（，t）+v（t）（3）

　　其中，v（t）為加性高斯噪聲。

2 小波包理論

　　小波分析是將任意信號f（t）表示為小波函數的線性組合，Mallat[6]在多分辨率分析的基礎上提出正交小波變換分解與重構的快速算法：信號f（t）的j層小波分解是將f（t）以尺度j變換到空間L2（R）的兩個正交子空間Vj和Wj上，由Vj得到離散逼近值cAj，由Wj得到離散細節值cDj，下層分解中以尺度j+1再將cAj分解到子空間Vj+1和Wj+1中，這樣不斷分解下去，實現對信號的多分辨率分解。

　　設{hn}n∈Z是正交尺度函數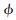（t）對應的正交低通實系數濾波器，{gn}n∈Z是正交小波函數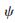（t）對應的高通濾波器，其中gn=（-1）nh1-n，則它們滿足以下兩尺度方程和小波方程：

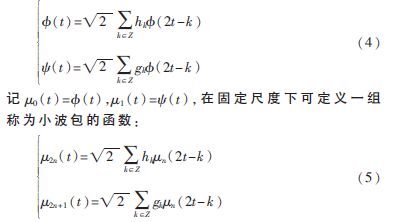
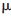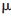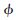　　遞歸定義的函數n（n=0，1，2...）稱為由正交尺度函數0=確定的小波包。

3 小波包閾值去噪

　　3.1 小波閾值

　　超聲回波信號中所含噪聲大多為高斯噪聲，噪聲對應的小波系數分布相近、個數多、幅值小。而回波信號經小波變換后可認為由信號產生的小波系數包含信號的重要信息，其幅值較大，數目較少。據此，設置一個合適的閾值，大于該閾值的小波系數判定為有用信號，予以保留；小于該閾值的小波系數判定為噪聲，予以剔除。最后將處理后的小波系數利用逆小波變換進行重構，恢復有效信號，達到去噪目的[7]。

　　小波變換由于分析窗的面積是固定的，高的時間分辨率對應差的頻率分辨率，針對超聲回波信號包含一定中、高頻率的時變信號這一特性，不能提供很好的頻率分析。小波包變換在多分辨率分析的基礎上對小波空間做了更精細的分割，特別是對高頻部分進一步分解。在小波包分解中，每一個高頻系數向量也像低頻部分一樣分解成為兩個部分，這種方法提供了更加豐富的分析方法，達到細致的刻畫效果，提高了超聲檢測信號的分析能力。

　　3.2 小波包分解與重構

　　3.3 小波包閾值規則

　　N為噪聲信號經小波分解得到的小波系數總和，?滓為噪聲信號均方差，閾值選擇規則[9]如下。

　　（1）Sqtwolog規則：采用Donoho和Johnstone統一閾值：

　　（2）Rigrsure規則：采用基于Stein無偏似然估計原理的自適應閾值。設p=[p1，p2，…，pN]，且p1≤p2≤…≤pn，p的元素為小波包系數的平方，按由小到大的順序排列。設R為風險向量，其元素為：

　　三種閾值規則各有特點，Sqtwolog閾值規則是將全部系數進行處理，因此去噪效果較強，但容易過度去噪，稱為“激進”規則，適合高頻部位；Rigruse閾值規則以及Minimaxi閾值規則是將部分系數進行處理，是較為保守的處理方法，可防止過度去噪，但也容易出現去噪不足，稱為“溫和”準則，適合低頻部分。

　　3.4 多閾值分段去噪

　　噪聲在頻率域上的分布主要集中在頻率較高的部分，在利用小波包去噪時，假如不同頻段信息采用同種閾值處理方法，或同一個頻段信息采用不同閾值處理方法都會影響去噪精度[10]。

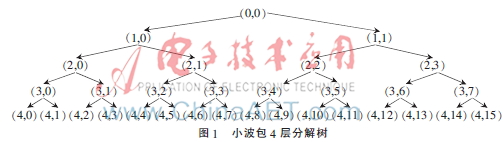
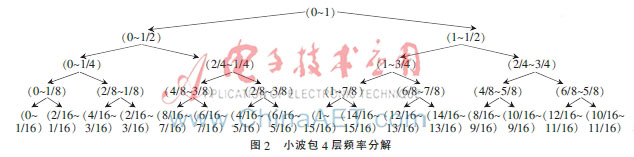
　　由圖1、圖2可以發現，小波包樹節點的自然順序與頻率順序存在不一致的現象。最低頻部分對應的是第一個節點，最高頻部分對應的是第九個節點。因此可以將一種多閾值分段去噪的方法應用于超聲信號檢測中。具體做法是：取低頻節點（4，0）為A段，高頻節點（4，8）為C段，剩余節點分在中頻段為B段，在A段采用Rigruse閾值規則，在B段采用Minimaxi閾值規則，在C段采用Sqtwolog閾值規則。

4 仿真實驗

　　基于式（2），取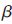0.4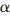，=25（MHz）2，fc=5 MHz，τ= 3.5 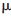s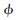，=1.8 rad，構建超聲回波信號。基于式（3），添加隨機高斯色噪聲，得到模擬含噪超聲回波信號。針對加噪后的信號，分別采用Sqtwolog閾值規則、Rigruse閾值規則、Minimaxi閾值規則和上文提到的多閾值分段規則進行去噪比較。其他條件統一為：采用sym4小波基，分解層數4層，軟閾值處理。仿真結果如圖3所示。

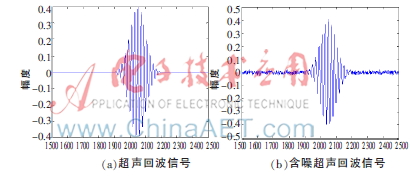
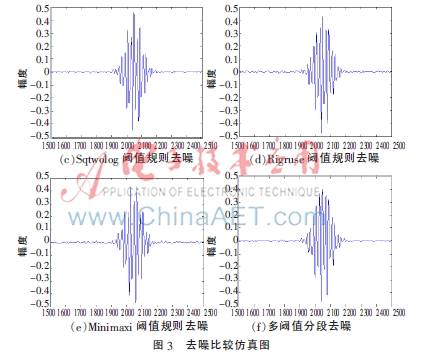
　　如圖3所示，（c）圖中采用Sqtwolog閾值規則，相比（b）圖含噪信號，有良好的去噪效果。但相比（a）圖原始信號，有用信號失真較為嚴重，屬“激進”去噪；（d）圖和（e）圖分別采用Rigruse閾值規則和Minimaxi閾值規則去噪，信號失真較小，但去噪效果不及Sqtwolog閾值規則，屬“溫和”去噪；從（f）圖中可看出，基于多閾值分段去噪的方法有用信號保留相對完整，整體去噪效果相對平滑。

　　為了更精確地區分這四種去噪方法的效果，將20組隨機高斯色噪聲加入超聲回波信號中，去噪處理前平均信噪比為15.910 7。選用信噪比（SNR）、均方根誤差（RMSE）、與原始信號的互相關系數（ρ）、平滑度（?酌）作為評價小波包閾值去噪對信號的處理效果[11-12]。信噪比為有用信號的能量與噪聲能量之比，信噪比越大越好；均方根誤差指重構后信號與原始信號的均方根誤差，其值越小表示去噪效果越好；互相關系數為原始信號與重構信號的方差，其值越接近1越好；平滑度是反映重構信號的平滑程度，平滑度越小則信號處理效果越好。比較結果如表1所示。

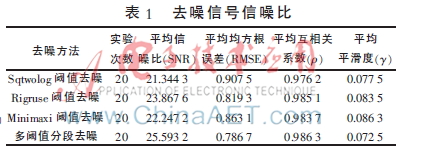
　　如表1所示，從信噪比和均方根誤差分析來看，在單閾值去噪方法中，Rigruse閾值規則去噪效果最明顯。但采取多閾值分段的方法進行去噪，比全局單閾值的方法要好。因為Sqtwolog閾值規則去噪更適合高頻去噪，而超聲回波信號的大部分有用信息在低頻部分，所以平均信噪比最差。Rigruse閾值規則去噪和Minimaxi閾值規則去噪在中低頻部分去噪效果良好，在超聲回波信號處理中優于Sqtwolog閾值規則去噪。多閾值分段去噪在高頻段采用了Sqtwolog規則，使其在有用信息含量較少的部分采用“激進”去噪，在有用信號大量集中的低頻段采用單閾值去噪效果最好的Rigruse規則，在中頻段采用相對“溫和”的Minimaxi規則，所以去噪效果最好；從互相關系數的數據分析中可以發現，采取Sqtwolog閾值規則其信號失真較嚴重，而多閾值分段去噪和Rigruse規則都對有用信號保留比較完整；從平滑度來看，Sqtwolog閾值規則去噪后較平滑，而Rigruse閾值規則是直接將一部分的高頻系數置0，雖很好地保留了信號的真實成分，但去噪后平滑度較差。從數據中可以看出，采用的多閾值分段規則進一步完善了Sqtwolog規則的信號處理效果，去噪后數據更加平滑，局部突變較小，更接近原始信號。

　　整體來說，四種不同的方法都能達到一定的去噪效果。但不同的閾值規則選取對最終去噪效果影響很大。本文通過分析單閾值規則去噪的各自優劣，結合Sqtwolog、Rigruse、Minimaxi這三種不同單閾值規則的表現而改進的多閾值分段去噪方法，使信噪比得到顯著提升，很好地保留了有用信號，整體去噪效果更平滑，特別適用于有用信息豐富的超聲回波信號處理。

5 結束語

　　本文通過將小波包分解按照頻率重新排列為高、中、低三個頻段，在不同頻段采用更加適合的閾值規則，進而將多閾值分段去噪應用在對超聲回波加噪信號的處理上。通過實驗仿真比較表明，多閾值分段去噪在超聲回波信號去噪中效果明顯，并最大程度地保留了有用信息，減少了信號失真，為解決實際超聲回波含噪信號的去噪問題提供了一種有效的信號處理方法。

　　參考文獻

　　[1] 羅雄彪，陳鐵群.超聲無損檢測的發展趨勢[J].無損檢測，2005，27（3）：148-152.

　　[2] 崔治.小波分析在超聲檢測信號處理中的應用研究[D].長沙：湖南大學，2012.

　　[3] 郭建峰.圖像小波閾值去噪方法研究[J].電腦知識與技術，2014（22）：5291-5292，5300.

　　[4] 鄭建國，石智，權豫西.非平穩信號的小波包閾值去噪方法[J].信息技術，2007，31（3）：16-18，55.

　　[5] 盧振坤.參數化的超聲回波模型及其參數估計[D].廣州：華南理工大學，2013.

　　[6] MALLAT S. Theory for multi-resolution signal decomposition： the wavelet represention[J]. IEEE Transactions on  Pattern Analysis and Machine Intelligence， 1989，11（7）：674-693.

　　[7] 張燕.超聲缺陷回波信號小波閾值去噪方法研究[D].南京：南京郵電大學，2012.

　　[8] 孫延奎.小波分析及其應用[M].北京：機械工業出版社，2005.

　　[9] 陳曉曦，王延杰，劉戀.小波閾值去噪法的深入研究[J].激光與紅外，2012，42（1）：105-110.

　　[10] 章浙濤，朱建軍，匡翠林，等.小波包多閾值去噪法及其在形變分析中的應用[J].測繪學報，2014，43（1）：13-20.

　　[11] 陶珂，朱建軍.多指標融合的小波去噪最佳分解尺度選擇方法[J].測繪學報，2012，41（5）：749-755.

　　[12] 李宗春，鄧勇，張冠宇，等.變形測量異常數據處理中小波變換最佳級數的確定[J].武漢大學學報（信息科學版），2011（3）：285-288.