0 引言

    LLC諧振功率變換器能夠?qū)崿F(xiàn)寬工作范圍內(nèi)的零電壓切換，且在輸入電壓和負載大范圍變化時開關(guān)頻率變化范圍較小，是一種當前備受關(guān)注的功率變換器。變頻調(diào)制是諧振變換器常用的調(diào)制方法，但其頻率變化范圍較寬，不利于磁性元件的優(yōu)化設計。

    自激移相調(diào)制（Self-Sustained Phase Shift Modulate，SSPSM）是由加拿大學者Mohamed Youseff提出的一種新的控制方法，該方法開關(guān)頻率變化范圍小，軟開關(guān)特性好，輸出調(diào)節(jié)能力強^[1]。文獻[2-6]研究了基于自激移相控制的全橋LCC變換器的基本原理和設計方法。將自激移相控制應用于LLC諧振變換器還具有較大的研究空間。

    本文將系統(tǒng)研究基于自激移相調(diào)制的全橋LLC變換器的工作特性。

1 全橋LLC變換器的工作原理

    圖1所示為全橋LLC變換器主電路，由開關(guān)網(wǎng)絡、諧振網(wǎng)絡、整流網(wǎng)絡等組成，調(diào)制器采用自激移相調(diào)制。

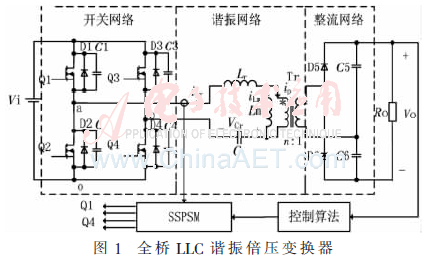
    圖2所示為自激移相調(diào)制的波形圖。該調(diào)制方法采用了兩個控制變量γ_a和γ_b，γ_a為反向諧振電感電流-i_Lr與開關(guān)管Q₂漏源電壓V_ao的相位差，γ_b為諧振電感電流i_Lr與開關(guān)管Q₄漏源電壓V_bo的相位差，相位角γ_a和γ_b的差值對應全橋開關(guān)電路輸出電壓V_ab的零電平相位角。自適應鋸齒波V_st為調(diào)制波，其歸零時刻與諧振電流-i_Lr的過零時刻相一致，V_st的幅值應保持恒定。V_ca和V_cb為兩路調(diào)制線，調(diào)制線與調(diào)制波相比較，并經(jīng)邏輯電路轉(zhuǎn)換，產(chǎn)生開關(guān)管的驅(qū)動信號。

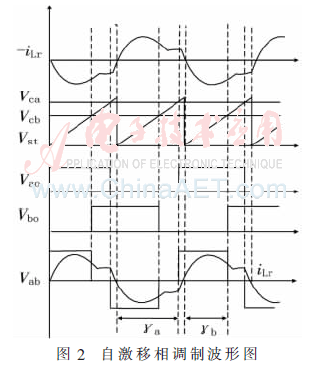
    自激移相調(diào)制有兩根調(diào)制線，通常需要保持上調(diào)制線恒定以作為參考基準，而下調(diào)制線動態(tài)變化。下調(diào)制線由變換器的輸出電壓等狀態(tài)量經(jīng)PI等控制算法解算得到，下調(diào)制線和鋸齒波相交時刻對應V_bo的上升和下降沿，則V_ab的脈寬主要受下調(diào)制線和自適應鋸齒波的控制。

    若保證V_ca小于三角波的幅值，即γ_a<180°，則能實現(xiàn)諧振電流i_Lr始終滯后于V_ab。該調(diào)制方式通過可控的角度γ_a來實現(xiàn)開關(guān)管的驅(qū)動信號超前于諧振電流，進而保證開關(guān)管ZVS零電壓開通。

2 LLC諧振變換器的建模

    采用基波分析法展開基于自激移相調(diào)制的LLC變換器的建模分析。基波分析法的思想是將變換器非線性環(huán)節(jié)的電壓、電流量用其基波成分近似替換，從而達到使變換器線性化的目的。

    根據(jù)LLC諧振變換器中各元件的功能的不同，可以將其劃分為開關(guān)網(wǎng)絡、諧振網(wǎng)絡和整流濾波網(wǎng)絡三部分。

2.1 開關(guān)網(wǎng)絡

    輸入電壓為V_in，開關(guān)網(wǎng)絡為一個全橋逆變器，橋臂中點輸出電壓(a、b兩點間電壓)v_ab(t)為一個方波。設定i_Lr(t)=I_Lr·sinωt為基準，由圖2中v_ab(t)和i_Lr(t)關(guān)系，可知：

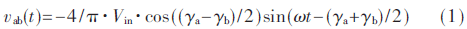
    則其有效值為：

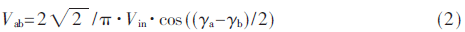
    故可將開關(guān)網(wǎng)絡近似等效為一個有效值為V_ab的正弦輸入電壓源。

2.2 整流濾波網(wǎng)絡

    設變壓器副邊電流為i_s。由于電流i_s經(jīng)過整流后的平均電流和負載電流I_o相等，則：

    v_s與i_s同相位，因此整流網(wǎng)絡可等效為一個純阻性負載R_eq。可以推導出R_eq的表達式為：

2.3 變換器的等效電路模型

    經(jīng)過以上簡化處理后，可以得到全橋 LLC諧振變換器的近似等效電路，如圖3所示。其中，R_ac=n²R_eq，為Req折算至變壓器原邊后的等效電阻。

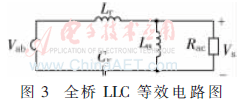
    根據(jù)基波等效電路，可得其傳遞函數(shù)：

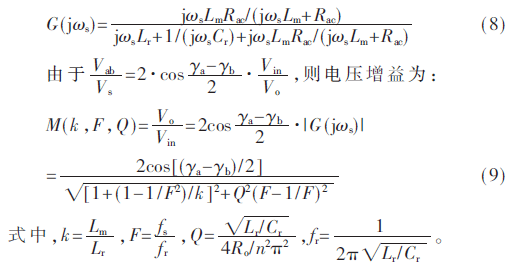
2.4 變換器的增益特性分析

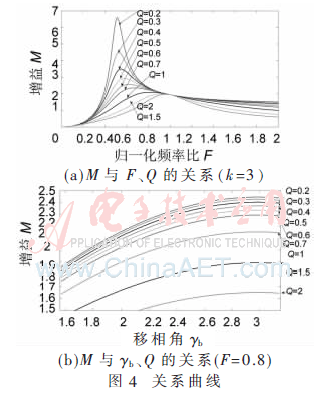
    根據(jù)得出的電壓增益表達式，通過MATLAB繪出相關(guān)圖形。圖4(a)為增益隨F和Q值變化的曲線圖，可見F=1時電壓增益幾乎獨立于負載，當開關(guān)頻率偏離諧振頻率時，增益隨著Q值的增大而減小。

    圖4(b)為增益隨γ_b和Q變化曲線圖，可見增益曲線隨著γ_b的增大而增大，隨著Q值的增大而減小。

3 自激移相調(diào)制下系統(tǒng)自振特性分析

    圖5給出諧振變換器的簡化結(jié)構(gòu)，由線性部分G(S)和非線性部分N(X)串聯(lián)。自振分析時r(t)=0。定義逆變輸出的一次諧波分量和反饋諧振電流信號的復數(shù)比為非線性環(huán)節(jié)的描述函數(shù)N(X)。諧振網(wǎng)絡的開關(guān)傳遞函數(shù)為G(S)。

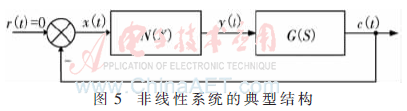
    非線性系統(tǒng)具有等幅振蕩的條件是等效的開環(huán)幅頻特性等于-1，即：N(X)·G(jω)=-1^[7]。在同一復平面內(nèi)作出自變量從0變化到∞時G(jω)和-1/N(X)的曲線，有：若G(jω)曲線不包圍-1/N(X)，則非線性系統(tǒng)穩(wěn)定；若G(jω)=-1/N(X)，則系統(tǒng)可能出現(xiàn)自激振蕩。但是并非所有交點都能構(gòu)成穩(wěn)定自激振蕩，只有-1/N(X)軌跡的進行方向是由G(jω)的包圍區(qū)過渡到非包圍區(qū)的交點才能構(gòu)成穩(wěn)定自激振蕩。

    由式(1)得非線性環(huán)節(jié)的描述函數(shù)為：

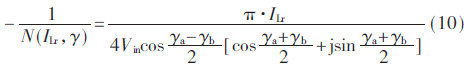
    取諧振電流為定值，在同一復平面上作出傳遞函數(shù)G(jω)和描述函數(shù)-1/N(X)的曲線，如圖6(a)所示。可知，當γ_a、γ_b∈[0，π/2]時，曲線無交點；當γ_a、γ_b∈[π/2，π]時，曲線有交點，因此系統(tǒng)在該范圍內(nèi)存在自振點。為了確定這些自振點是否穩(wěn)定，作出γ_a=γ_b=3π/4時傳遞函數(shù)G(jω)和描述函數(shù)-1/N(X)的曲線，如圖6(b)所示。

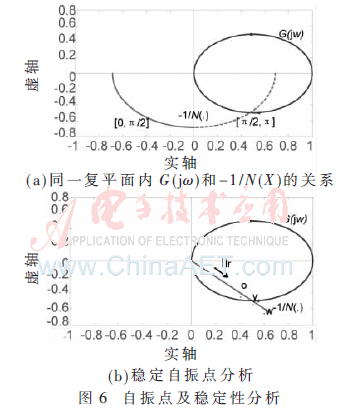
    隨著諧振電流的增大，-1/N(X)的軌跡從G(jω)的包圍區(qū)過渡到非包圍區(qū)。

    當諧振電流變化導致y點移到G(jω)包圍區(qū)的w點時，系統(tǒng)狀態(tài)不穩(wěn)定，振蕩變大，并向y點移動并最終處于穩(wěn)定狀態(tài)。當y點移動到G(jω)非包圍區(qū)的o點時，系統(tǒng)處于穩(wěn)定狀態(tài)，自振振幅減小，直至衰減為零，使系統(tǒng)重新回到y(tǒng)點處的狀態(tài)。綜上分析，該系統(tǒng)在γ_a、γ_b∈[π/2，π]時存在穩(wěn)定的自振點。

4 實驗研究

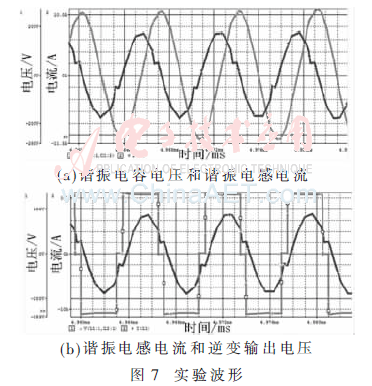
    根據(jù)前文理論，設計符合以下要求的變換器：輸入電壓V_in=270 V，輸出電壓V_out=1 200 V，功率P=800 W，開關(guān)頻率f_s=140 kHz。取F=1.1，k=3，Q=0.2，r_a=5π/6，γ_b∈[π/2，5π/6]。根據(jù)本文分析進行實驗，諧振參數(shù)：L_m=111.93 μH，L_r=37.31 μH，C_r=28.05 μH。圖7(a)為諧振電容電壓（峰值較大者）和諧振電感電流的波形圖，可見兩者均進行等幅的周期振蕩；圖7(b)為逆變輸出電壓（方波）和諧振電感電流的波形圖，可以看出諧振電流滯后于諧振電壓，變換器實現(xiàn)軟開關(guān)特性。

5 結(jié)論

    自激移相調(diào)制全橋LLC變換器可大幅降低開關(guān)損耗，有效提高工作效率。本文對基于自激移相調(diào)制的全橋LLC工作原理進行了詳細分析，并利用基波分析法對其進行數(shù)學建模，推導分析其電壓增益特性；將非線性理論中的描述函數(shù)法應用到自激移相調(diào)制LLC變換器上，深入分析系統(tǒng)的自振特性；最后通過仿真驗證了該調(diào)制方式的有效性。

參考文獻

[1] YOUSSEF M Z，JAIN P K.Design of a front end series parallel resonant converter with self-sustained phase shift modulation controller[J].IEEE Transactions on Power Electronics，2004，19(2)：328-333.

[2] 廖鴻飛.自持振蕩移相控制的全橋LCC諧振變換器的研究[D].廣州：華南理工大學，2007.

[3] PAHLEVANINEZHAD M，EREN S.Self-sustained oscillating control technique for current-driven full-bridge DC/DC converter[J].IEEE Transactions on Power Electronics，2013，28(11)：5293-5310.

[4] YOUSSEF M Z，JAIN P K.A review and performance evaluation of control techniques in resonant converters[C].The 30th Annual Conference of the IEEE Industrial Electronics Society，Busan：IEEE Conference Publications，2004：215-221.

[5] YOUSSEF M Z，PINHEIRO H，JAIN P K.Self-sustained phase shift modulated resonant converters：modeling，design，and performance[J].IEEE Transactions on Power Electronics，2006，21(2)：401-414.

[6] YOUSSEF M Z.Control and modeling of high frequency resonant DC/DC converters for powering the next generation microprocessors[D].Queen′s University from Canada，2005.

[7] 吳俊娟，孫孝峰，鄔偉揚.基于描述函數(shù)法的諧振變換器自持振蕩研究[J].電力電子技術(shù)，2011，45(2)：53-55.