摘 要: 在數據采集過程中結合網格聚類算法提高計算效率,為了保存采樣數據的分布特點引入權值。根據類別中心密度高、權值大的特征采用尋找連通分量的方法初步確定聚類中心,在此基礎上結合自適應免疫算法,動態地確定聚類中心及其類別數。進而使FCM算法跳出局部最優,最大可能地得到全局最優解。
關鍵詞: 聚類;權值合理性;自適應免疫算法;連通分量
FCM算法是當前最受關注的聚類方法之一。本質上,FCM算法是一種初始化數據與聚類結果之間的映射方法,其求解過程采用一種爬山技術進行迭代來尋找局部最優解。當初始化完成后,相應的聚類結果就已經確定了。所以FCM算法對初始化數據比較敏感,有可能陷入局部最優解,無法得到全局最優解。
針對此問題目前主要的解決方法有兩種:(1)在聚類的過程中進行全局隨機搜索[1],Xinchao等人采用模擬退火算法。對當前聚類所獲得的結果采用退火計劃進行擾動,并以一定的概率接受擾動后的結果為當前最優解,進而跳出局部最優解。此算法要求足夠多的擾動次數,配以嚴密的擾動計劃來獲取全局最優解,即此算法要求大量的計算。(2)改善FCM算法的初始化條件,選擇合適的聚類中心[2]。在初始化問題上,本文受第二種方法啟發,把網格劃分加權[3]、尋找連通分量、自適應免疫算法[2]相結合。對原始數據進行初始化處理,動態尋找初始類別數和相應的聚類中心。進而跳出局部最優,最大程度地找到全局最優解。本文將原始的FCM算法和改進的FCM算法進行對比分析。實驗表明,該改進方法能夠有效地降低時耗,提高聚類收斂速率。



2 改進的FCM算法
2.1 確定初始化聚類中心及類別數
(1)引入網格加權
將FCM算法與網格聚類的方法相結合,目的是引入網格聚類的優點:在處理數據時與數據對象的數目無關,只與每維空間所劃分的單元數目有關,保證聚類方法的高效性。在FCM算法中引入權重,對于網格密度大的空間,可以賦予相應大的權重,如定義3。最大程度保存原始數據分布特點,保證聚類結果的有效性。
(2)利用權值尋找連通分量法,確定初始化聚類中心
類別中的數據在一定范圍內是密集的,即相應的網格數據之間連通,并且相應的密度權值從最高密度中心向外遞減,密度權值最大的網格肯定包含于某一類別。步驟如下:
①找到權值最大的網格,遞歸尋找所有與之連通的網格。遞歸結束需滿足以下條件:沒有與之相連通的有數據的網格;雖然存在與之連通的網格,但是該網格的權值大于當前網格的權值。
②把步驟①中找到的連通網格看成一個初始類,并刪除選中的節點。然后重復上面的步驟,直到所有的數據網格都被處理完為止。
(3)對初始化聚類中心,與自適應免疫算法[2]進行結合。把聚類中心點看成是抗體,把相應的數據點看成是抗原。該抗體能夠識別周圍一定范圍內的抗原。其中?著,?滓是預先確定的門限值。具體步驟如下:
①對中心進行加權,權值以此中心所識別的抗原個數為依據。
②遍歷所有抗原計算其對于各抗體的親和度,并根據式(3)進行相應的變異。
變異率與抗原與抗體之間的距離成正比,與抗原的權值成反比,與親和力成反比,根據式(4)進行計算。
③把抗體之間的距離小于?著的抗原進行合并,形成記憶細胞。
④重復②、③直到無滿足條件的操作為止。
⑤去除不同記憶細胞中距離小于?滓的個體,即對其進行合并。所形成的新記憶細胞就是最后的初始化聚類中心,記憶細胞的個數就是初始化的類別數。
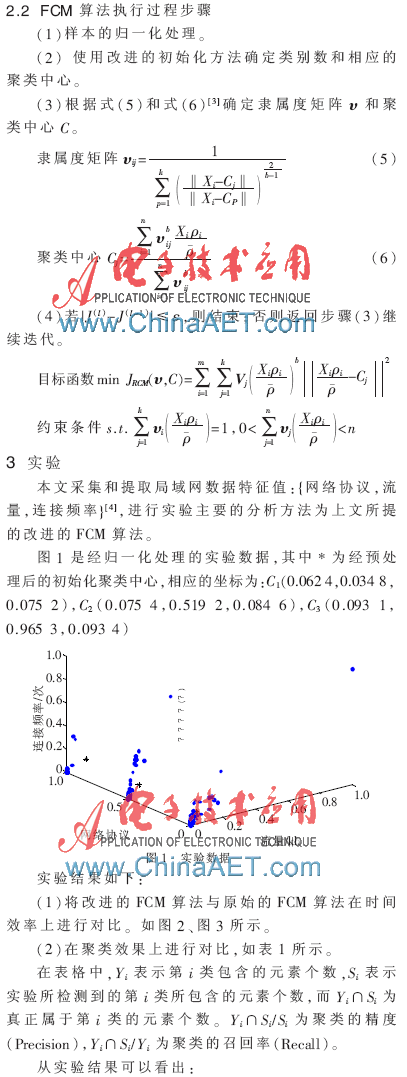
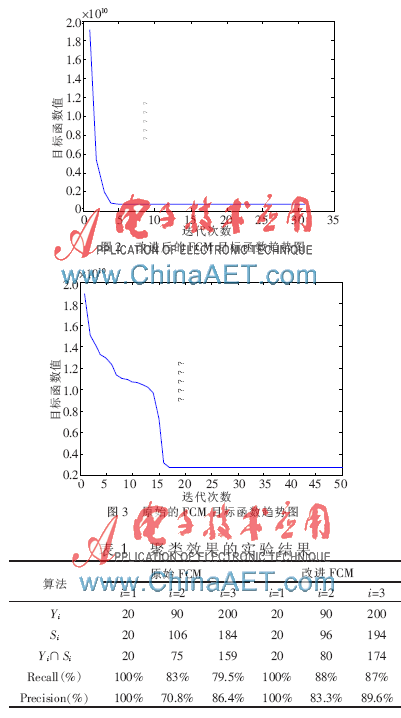
(1)在改進的FCM算法中,計算過程只迭代了31次出結果。而原始的FCM算法迭代了74次,才出結果。在時間效率上,改進的FCM算法有明顯的提高。
(2)改進的FCM算法在迭代過程中比較平穩,并且收斂的速度也比較快。然而未改進的FCM算法雖然總的趨勢也是收斂的,可是收斂的速度存在一定的波動。
本文針對FCM算法中存在的計算時耗高,對初始化數據敏感,容易陷入局部最優的問題,引入網格聚類,加權計算,尋找連通分量,自適應免疫算法等方法并采用初始化預處理的方法,對其進行一定的改進。在試驗中采集局域網中的數據包使實驗數據隨機分布,存在局部最優解。與原始的FCM算法進行對比試驗,結果表明,改進的FCM算法在時間效率和收斂速度上都有明顯的提高,改進的FCM算法是有效的。
參考文獻
[1] XINCHAO Z. Simulated annealing algorithm with adaptive neighborhood[J]. Applied Soft Computing, 2011,11(2):1827-1836.
[2] SZABO A, CASTRO L N D, DELGADO M R. FaiNet: An immune algorithm for fuzzy clustering[C]. in Fuzzy Systems (FUZZ-IEEE). 2012 IEEE International Conference on. 2012.
[3] HATHAWAY R J, HU Y. Density-weighted fuzzy c-means clustering[J]. IEEE Transactions on Fuzzy Systems, 2009. 17(1): 243-252.
[4] XING W, ZHAO Y, LI T. Research on the defense against ARP spoofing attacks based on Winpcap[C]. in Education Technology and Computer Science(ETCS), 2010 Second International Workshop on, 2010.

