0 引言

    隨著科技的飛速發展，信息技術已經成為了人們生活工作不可或缺的一部分，隨之而來的信息安全隱患成為了當前亟待解決的問題。公鑰密碼體制在信息安全領域的重要性不言而喻，橢圓曲線密碼體制在經過多年的研究成熟之后逐漸成為了新一代的公鑰密碼標準。由于高度密集的運算特性，公鑰密碼處理器在速度、靈活性、面積資源消耗等方面存在著較大矛盾。本文基于對橢圓曲線體制層次化運算特性的深入研究，通過對底層運算進行算法優化和單元結構兼容，設計了一種基于改進的radix-4交錯模乘算法的統一模運算單元，達到提高橢圓曲線處理器運算速度、靈活性和優化底層單元資源消耗的目的。本文對模加減和模除運算進行了優化和基于模乘單元的兼容設計。模除的結構復雜且調用率低，傳統的兼容設計思路是在模除單元基礎上實現模乘和模加減，或者在模乘基礎上擴展結構實現模除。這種設計往往出現資源浪費的問題。本文提出的改進的radix-4交錯模乘單元，能夠在不增加大位寬加減運算結構的基礎上，直接適配plus-minus模除和模加減，有效解決了資源浪費的問題。

1 模乘加算法分析

1.1 算法兼容性研究

    二元域與素數域運算的差異體現在運算規則上，素數域的所有運算都是有進位的，而二元域的運算則約束在對應位之中不存在進位，只是按位異或操作。目前業內出現了很多支持雙域操作的結構統一的運算架構，主要的策略有三種，一種為在素數域運算架構基礎上加入部分二元域專用的結構，以此來實現雙域操作；一種則是在主流的CSA加CPA結構基礎上，直接取用CSA的本位作為二元域輸出；一種為直接大素數域進位加法器中加入進位屏蔽信號，來實現無進位加法，即二元域加法。總之，二元域與素數域運算無論是在算法層次還是硬件結構層次都具有優秀的兼容性。

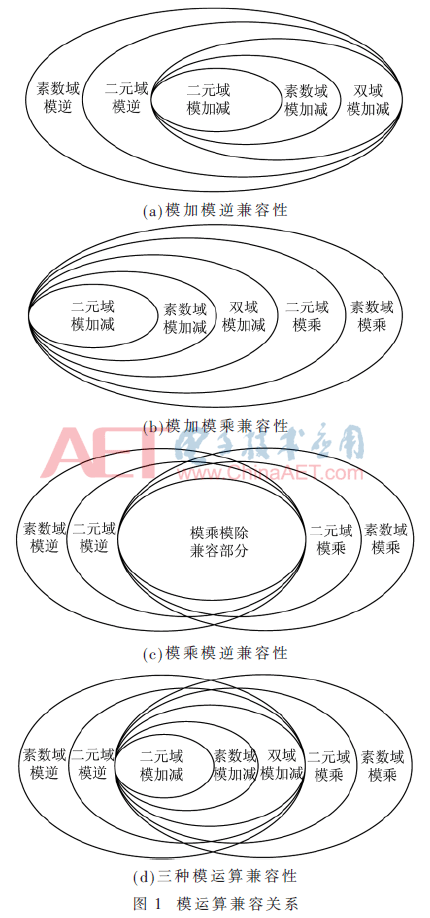
    綜上所述，有限域層運算無論是在模運算內部操作還是運算域方面都具有較好的兼容性。圖1是模運算系統的兼容關系。如圖所示，模乘加完全兼容于模乘與模逆算法。但是，模乘與模逆的兼容性關系根據算法的不同有可能是：模乘完全兼容模逆、模逆完全兼容模乘或二者部分兼容。素數域的運算均能較好地兼容相應的二元域運算。以上主要討論了有限域層運算在單元數據路徑上的結構兼容性。而它們在存儲單元方面也有較好的兼容性。有限域層各種運算所涉及到輸入數據中間變量情況如表1所示。

    由表1中信息可知，三種運算的數據輸入均為相同規格輸入，可以復用相同的寄存器，中間變量牽扯到的U、V在三種運算中皆為運算位寬加1~3 bit的進位，因此結構完全可以復用，而模逆/除運算中的標志位β、α根據它們在算法中的定義，其極限數據長度有限，與A、B、p、U、V等數據長度不在同一量級。因此三種運算所涉及的寄存器可以達到很高的復用率。為了適配NIST規定的標準，本文設計的運算位寬要兼容576 bit以內的任意長度的雙域運算。

1.2 算法分析及改進

    如表2所示，算法1所述的基交錯模乘，在運算過程中進位鏈太過復雜，如“C=C+b₀·A+b₁·2·A(mod p)”要進行三個數據的算術加法和模約減運算。且其中一項“0<b₁·2·A<2p”，導致這一步運算的結果0<C<4p，則需要進行C-0·p、C-1·p、C-2·p、C-3·p的四種模約減運算，硬件實現上需要兩級CSA一級CPA。

    如果能夠在累加之前預先計算出b₁·2·A(mod p)，就可以將2.1操作的結果約束到0<C<3p而后再約減，從而降低約減的運算復雜度，簡化電路。另外考慮到模乘操作本質上是一連串的加法和約減運算的合集，加法與模減的先后順序并不會影響到最終的結果。即，C=C+b₀·A+b₁·2·A(mod p)中的b₀·A和b₁·2·A可以分開進行加和約減。因此可以將乘數B分為奇數位和偶數位進行并行計算，結尾時再將兩個部分乘積進行加和約減得到最終結果。該種并行運算操作可以將2.1步所需要的三輸入加法器改成二輸入加法器，進而縮短關鍵路徑。但是如果奇偶分開之后2.2步的提前約減就會變得相對復雜，此處的操作順序與流水加速實現方法將在3.2.3進行詳細描述。改進的并行2n基交錯模乘算法如表3所示。

　　在算法2中，O為乘數B奇數位掃描的部分和，E則為偶數部分和。在算法2中只有2.3的模約減數據A1的約束范圍是0<4A₁<4p，需要進行C-0·p、C-1·p、C-2·p、C-3·p的四種模約減運算。其余所有操作均約束在2p以內，不需要C-2·p、C-3·p操作，降低算法約減代價。同時，簡化子運算過程勢必會降低對應硬件結構的復雜度，將三輸入加法器改為并行二輸入加法器來實現，降低了數據路徑的延遲。

需要注意的是，以上兩種算法均為雙域統一的模乘算法，且之前的分析均為基于素數域的分析。基于二元域的運算相對簡單，將所有的進位信號進行屏蔽即可，兩者的具體區別將在后續的硬件設計過程中詳細描述。綜上所述，本小節對兩種算法在算法結構上進行了一定的改進，兩種類型的模乘算法各有利弊，具體的區別，如運算效率、功耗、面積將在后面的小節進行更為詳細的分析比較。

2 流水線分析

    對算法2的循環部分分析可知，核心循環部分主要有三個步驟。

    (1)O←0+b₀·A₁ mod p與E←E+b₁·A₂ mod p mod p，完成掃描結果的累加；

    (2)A₁←4·A₁ mod p，奇數部分累加值更新；

    (3)A₂←2·A₁ mod p與B←B<<2，偶數部分累加值更新與乘數B移位。

    如果按照這樣的步驟分析，每個輪循環需要3個時鐘周期才能完成，且步驟(1)與步驟(3)有數據相關性無法完成全流水。若將步驟(1)中的兩個累加過程進行分步執行就可以防止這種數據相關性導致的流水障礙。即將算法步驟調整為兩步：

    (1)O←O+b₀·A₁ mod p，A₂←2·A₁ mod p，完成奇數位累加及偶數位累加數據更新。

    (2)E←E+b₁·A₂ mod p，A₁←4·A₁ mod p，B←B<<2，完成偶數位累加、奇數位累加數據更新及乘數B移位。

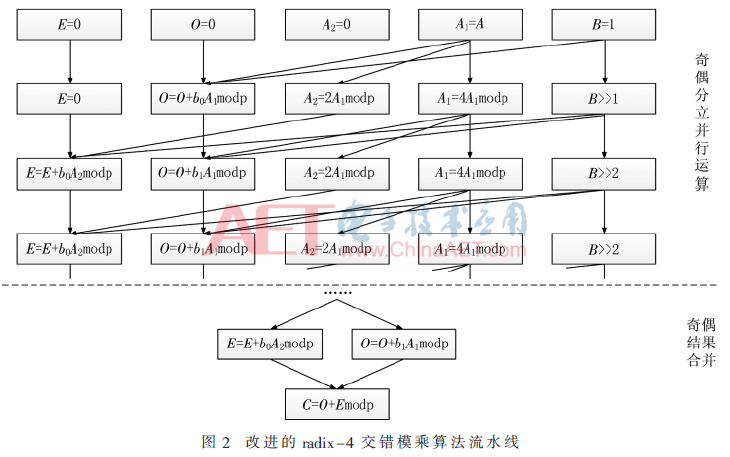
    進行上述改進之后，步驟(1)與步驟(2)可以流水并行執行。在第一個clk來臨時，步驟(1)的O←O+b₀·A₁ mod p、A₂←2·A₁ mod p與步驟(2)的A₁←4·A₁ mod p同時執行。這三者產生的結果，分別是O的更新值，用于E累加的A₂，用于O累加的A₁。第二個clk開始，O←O+b₀·A₁ mod p需要的O與A₁上一周期已經得到；E←E+b₁·A₂ mod p需要的A₂也在上一周期得到；A₂←2·A₁ mod p所需要的A₁已經在上一周期更新；A₁←4·A₁ mod p所需的A₁也在上一周期更新。因此步驟(1)可以和步驟(2)并行運行，但是需要注意的是步驟(2)的運算輪次慢于步驟(1)一個時鐘周期。則算法更新為表4所示的算法3。

    為使該算法的流水線描述更加詳細，圖2對該算法每個時鐘每個模塊的運算以及數據流向進行詳細標注描述。其中橫向為同一時鐘周期完成的操作，縱向為時間流逝方向，箭頭表示數據流向。

    由圖2可知，算法3可以實現全流水，相對于蒙哥馬利模乘，其運算效率更高。但是由于其數據高低位之間存在嚴格的數據相關性，難以實現高低位數據之間的并行加速改進。

3 硬件電路設計

3.1 模乘單元研究

    根據前文對算法3的分析以及流水線的設計，可知radix-4交錯模乘算法的核心運算主要包括以下4個：

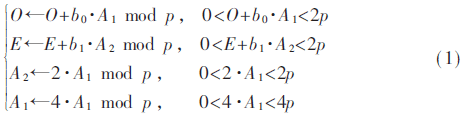
    由上式可知，這四種運算以A₁←4·A₁ mod p的約減過程最為復雜，需要判斷約減3p、2p、p或者不約減，需要三個并行的約減CPA。A₂←2·A₁ mod p最為簡單，可以通過移位代替2A₁運算，而后只需要進行是否減p判斷即可。這4種運算的具體結構如圖3所示。

    4種結構思路均為通過并行多路運算提前完成加np約減預計算，而后根據不同加np路徑的進位進行判斷并選擇正確的約減結果。該種結構面積會有一定的增大，但是運算效率極高。前文已經提到了，將原算法1的C=C+b₀·A+b₁·2·A(mod p)分解為并行運行的O←O+b₀·A₁ mod p與E←E+b₁·A₂ mod p。在算法運算邏輯上雖然分開的兩者可以并行，但實際上E←E+b₁·A₂ mod p的累加比O←O+b₀·A₁ mod p的累加要落后一個周期，即比原來的結構多用2～3個時鐘，但是相對整個運算過程的用時，可以忽略不計，同時圖3這種改進的結構比原結構的關鍵路徑更短，綜合考慮改進后的結構更優化。

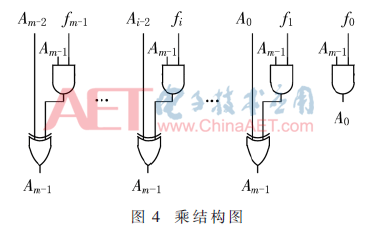
    圖3所有結構均為雙域統一的模乘運算單元。下面以A₁←4·A₁ mod p的結構為例，分析二元域運算原理，此時的運算變為A₁(x)←x²·A₁(x) mod f(x)，即需要進行兩次連續的x乘。首先通過field信號將所有CPA中的進位信號屏蔽，同時將CSA中的輸入進位全部拉低，將CPA和CSA的本位輸出均轉化為兩個輸入數據的異或。而后將兩個輸入，一個定義為A₁(x)<<1，另一個定義為f(x)或0。選擇f(x)或0的判斷條件是A₁(x)左移前的最高位。圖4是x乘A₁(x)←x¹·A₁(x) mod f(x)的硬件原理圖。二元域的模除運算運用同樣的原理，將除2模變成x除運算。

    本文設計基于radix-4交錯模乘算法的總體硬件結構，如圖5所示。

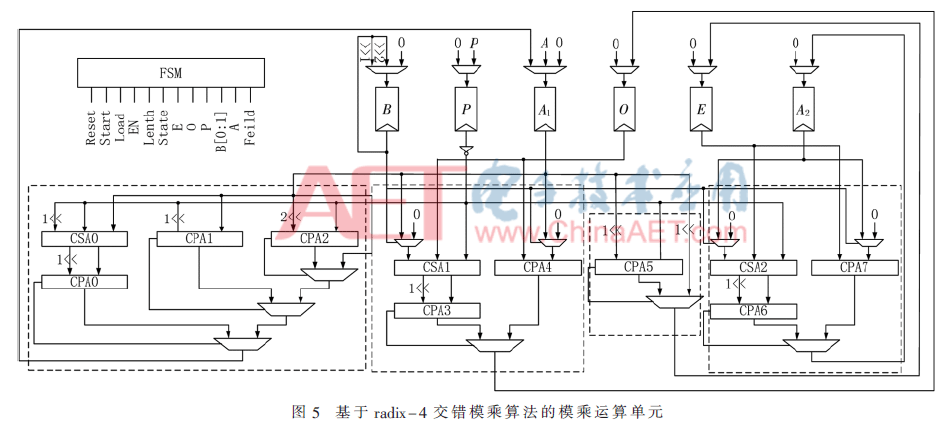
3.2 模除單元研究

    根據p-m 算法分析可知，該算法需要經歷“數據更新路徑裁決”（J-path）和“數據更新”（U-path）兩個過程。p-m算法引入了兩個變量ε=min(α，β)和λ=α-β，其中α、β分別表示，中間變量A、B的階，但在算法中不會直接使用α、β，而是使用兩者的變化量ε、λ。ε、λ的引入可以代替經典歐幾里得模除算法A、B大小的比較，使得J-path的路徑復雜度大幅度降低。算法4如表5所示，表6是算法4的判斷條件及路徑選擇。

    這種算法在硬件結構設計時較傳統蒙哥馬利模除算法具有較大優勢。該算法的J-path路徑結構比較簡單，不需要依靠大位寬CPA，從而一定程度上降低了相應延遲，同時也節省了面積資源。但是其判斷條件及數據更新的關系較蒙哥馬利模乘算法稍顯復雜，規律性較低，在控制路徑設計時可能會導致復雜度上升。不過這兩種結構的關鍵路徑均不在控制路徑上，其對單元的整體性能影響微乎其微。而更新過程也分為相對獨立的兩部分。其中U-pathA主要是運算數據的更新，U-pathB主要是路徑裁決信息的更新(B←A，E←O為簡單的賦值運算，不作考慮)。

    通過分析表6中的不同運算可以發現。U-path與J-path之間是有數據相關性的，不能采取流水線劃分。J-path的路徑延遲由小比特的加減法和數據選擇器構成；而U-path則由大位寬的加法器和數據選擇器構成。兩者的延遲不在同一量級。如果采取流水線加速策略，將J-path和U-path劃分為兩級流水，會出現運算頻率提升有限而控制路徑復雜度大幅度提升的情況。因此本文并未對p-m模除算法進行流水線加速設計，而是采取“相似路徑整合，不同路徑并行，統一數據選擇”的策略。即將相似運算進行結構兼容，不能兼容的則并行運算，并根據判斷條件選擇出最終的正確結果。圖6給出了該模除算法的結構簡圖。主要由I/O接口、控制狀態機和數據路徑構成。數據路徑包括J-path數據更新裁決路徑、U-pathA數據更新路徑、U-pathB裁決信息更新路徑。

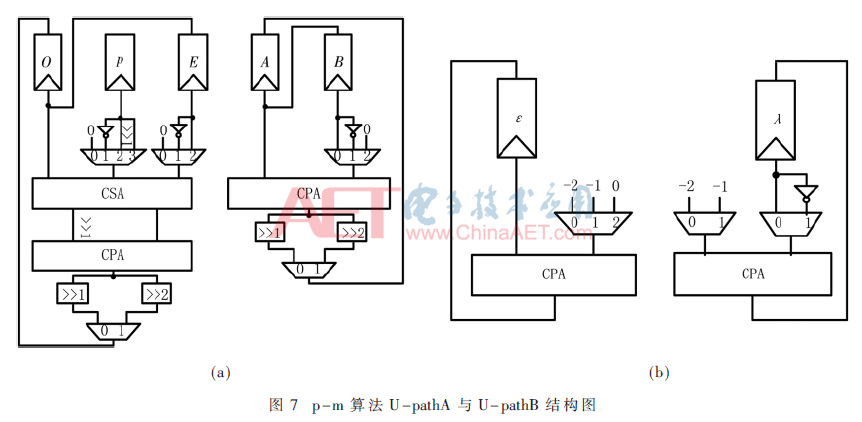
    面對表6給出的各條路徑進行運算分析和歸納分類。由于該算法與radix-4交錯模乘算法的兼容性主要體現在U-pathA中，此處著重分析U-pathA的相關操作。U-pathA操作可以歸納為一種算術移位運算Z←(X+Y)/n和三種模移位運算Z←X/2 mod p、Z←X/4 mod p、Z←(X+Y)/4 mod p。其中三種模移位運算在結構實現上比2 bit掃描的蒙哥馬利模除算法中的Z←4 X mod p等模約減運算簡單得多。因為0<4X<4p需要通過多次p減運算，最終通過進位判斷正確結果，消耗的硬件資源是3個三輸入加法器。完成(X+Y)/4 mod p需要進行四種運算，而后對結果進行左移兩位操作。但是與Z←4 X mod p路徑選擇方式不同，該運算的選擇信號與X、Y、p的末尾2 bit數據有關。因此不需要將這四種運算并行實現后對結果進行選擇，而是在輸入端就選擇+np，僅需一個3輸入加法器就可以實現。在此基礎上本文設計了如圖7(a)所示的U-pathA結構圖。U-pathB的結構為小位寬的加法，結構如圖7(b)所示。J-path的結構與統一模運算單元的兼容性并不強，且結構簡單、占用資源少，在此不進行詳細描述。

    模除運算的核心運算部分在于U-pathA，其主要運算由一種算術移位運算Z←(X+Y)/n和三種模移位運算Z←X/2 mod p、Z←X/4 mod p、Z←(X+Y)/4 mod p構成。由于運算原理的不同，模移位運算的選擇信號由最低位而不是最高位進位確定，因此可以在運算之前就可以根據運算數據的尾數確定運算正確路徑。且由于后三種操作不會在一輪運算中同時出現，因此這三者可由同一結構實現。圖8為U-pathA模移位運算路徑在radix-4模乘單元中的映射。圖8中虛線框中的CSA1、CPA3以及輸入數據選擇器一同完成“Z←X/2 mod p”、“Z←X/4 mod p”、“Z←(X+Y)/4 mod p”等運算。根據表6中對算術移位的路徑分析可知，當Z←(X+Y)/n中的n為2時，X+Y的最后1 bit必為0；當n為4時，X+Y的最后2 bit必為00。因此該路徑只需一個2輸入CPA即可完成，如圖8中右虛線框所示。

    J-path與U-pathA的路徑不在結構兼容考慮范圍之內，在此不再詳述。如圖9所示為基于radix-4交錯模乘算法的統一模單元結構圖。下面以“X+Y”、“A₁←4·A₁ mod p”、“O←(O+E)/4 mod p”為例描述統一模運算單元的模加、模除、模乘功能。其中紅色部分表示“X+Y”，通過“CSA1+CPA4”與“CPA5”分別實現是否“減p”的運算，而后通過數據選擇器完成數據更新。綠色部分為“A₁←4·A₁ mod p”路徑，其“CSA1+CPA1”、“CPA2”、“CPA3”分別完成A₁←4·A₁-3 p、A₁←4·A₁-2 p、A₁←4·A₁-p，而后根據三個CPA的進位確定正確輸出結果。“O←(O+E)/4 mod p”的運算路徑由“CPA4+CSA1”、“CPA5”以及輸入端的數據選擇器完成“-p”或“-0p”以及“右移2bit”的操作，其用到的結構與“X+Y”相同，只有輸入選擇器配置不同，在此不再進行額外標注。

4 性能分析

    文獻[1]～文獻[5]中對模運算單元進行了類似的模單元設計。為了性能對比的公平性和可靠性，本文將這些設計在相同的域長度下基于Xilinx Vitex-7 200T FPGA平臺進行了邏輯綜合，具體結果如表7所示。其中效能定義為：1/(Area×Time)，并對其進行了歸一化。

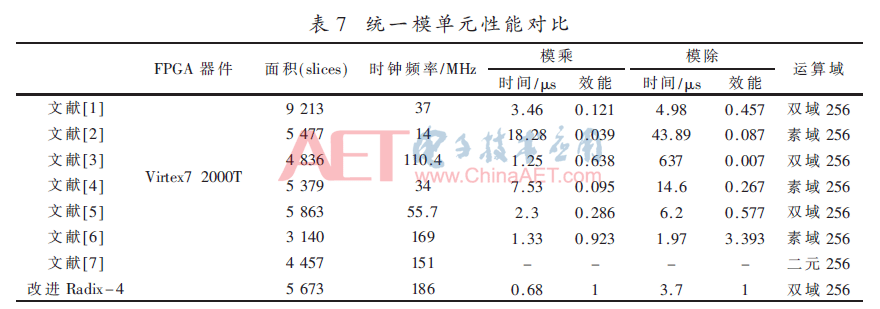
    通過對表7進行詳細分析可得到如下結論。

    (1)靈活性

    本文提出的統一模運算單元可以實現576 bit以內任意位寬的雙域有限域模運算，具有極高的靈活性。文獻均有較高的靈活性，可以滿足NIST提出的標準模式。而文獻[6]、[2]、[4]、[7]為固定結構，不具可重構性，難以滿足橢圓曲線密碼體制多樣化的應用需求。

    (2)面積資源消耗

    本文提出的統一模運算單元在Vitex-7 2000T的面積為5673 slices。文獻[6]、[7]、[4]、[3]比之較小，但是前三者為固定的運算位寬，且不能完成雙域運算，在靈活性上與本文不具有可比性。而對于文獻[2]，本文無論是在運算頻率還是模乘模除的運算時間上均比之優化。

    (3)運算速度與能效

    本文從算法和硬件設計層次對radix-4模乘算法進行了改進，將結構關鍵路徑分解重新規劃算法流程，并實現了全流水設計，在速度上具有一定的優勢。本設計的運算頻率在上述文獻中是最高的，效能除文獻[6]的模除外，為最高。但一方面文獻[6]中的結構不具有可重構性，另一方面，模除運算的調用頻數極低。所以在運算速度方面，本文提出的結構具有較大優勢。

    綜上所述，本文提出的統一模運算單元具有較高的運算速度、較好的靈活性，同時在面積資源消耗上進行了模單元兼容優化，并取得了一定的成效。而且該結構可以滿足目前國際國內橢圓曲線體制任意標準的底層模運算，能夠較好地移植到各種ECC處理器中，具有較好的適應性。

    前文已經在65 nm CMOS工藝下，通過DC對統一模單元進行了綜合，改進的radix-4統一模單元面積為223 761 μm2，時鐘周期為526 MHz。

    但相關研究實現方式大都在FPGA上進行實現，少有進行ASIC測試。目前相關的ECC處理器的ASIC設計時鐘周期多在300～500 MHz，而這些ECC處理器的關鍵路徑多由模單元決定。通過比較發現，本文設計的結構在速度和靈活性方面具有優勢。通過將本文提出的結構替換到相關ECC處理器中大多能實現一定的工作頻率優化。

5 結論

    本文提出了一種基于改進的radix-4交錯模乘算法的高速可重構統一模單元，該結構支持576 bit以內的任意長度雙域可重構模乘、模除和加減運算。不同于傳統統一模單元以模除單元為基礎的設計，該結構以模乘單元為基礎設計實現，具有較高的資源利用率，為統一模運算單元的設計提供了一定的參考。

參考文獻

[1] LEE J W，CHUNG S C，CHANG H C，et al.Efficient power-analysis-resistant dual-field elliptic curve cryptographic processor using heterogeneous dual-processingelement architecture[J].IEEE Transactions on Very Large Scale Integration Systems，2013，22(1)：49-61.

[2] DALY A.An FPGA implementation of a GF(p) ALU for encryption processors[J].Microprocessors & Microsystems，2004，28(5)：253-260.

[3] SAKIYAMA K，PRENEEL B，VERBAUWHEDE I.A fast dual-field modular arithmetic logic unit and its hardware implementation[C].IEEE International Symposium on Circuits and Systems，2006.ISCAS 2006.Proceedings.IEEE，2006.

[4] GHOSH S，MUKHOPADHYAY D，ROYCHOWDHURY D.Petrel：power and timing attack resistant elliptic curve scalar multiplier based on programmable，GF(p) arithmetic unit[J].IEEE Transactions on Circuits & Systems I Regular Papers，2011，58(8)：1798-1812.

[5] LIU Z，LIU D，ZOU X.An efficient and flexible hardware implementation of the dual-field elliptic curve cryptographic processor[J].IEEE Transactions on Industrial Electronics，2017，PP(99)：1-1.

[6] MARZOUQI H，AL-QUTAYRI M，SALAH K，et al.A high-speed FPGA implementation of an RSD-based ECC processor[J].IEEE Transactions on Very Large Scale Integration Systems，2015，24(1)：151-164.

[7] MORALES-SANDOVAL M，FEREGRINO-URIBE C，ALGREDO-BADILLO I.An area/performance trade-off analysis of a GF(2m) multiplier architecture for elliptic curve cryptography[J].Computer & Electrical Engineering，2009，35(1)：54-58.

作者信息:

陳  琳，唐  俊，曲彤洲，尹安琪

(信息工程大學，河南 鄭州450000)