0 引言

    近年來，光伏發電(PV)在電力系統中的比例逐漸增加，同時電動汽車(EVs)也有逐漸取代內燃機車(ICE)的趨勢，這些都導致了電力系統中存在不確定性因素^[1-2]。概率潮流（PLF）可用來評估包含上述不確定性因素的廣義電力系統的穩態系統性能。在PLF研究中，輸入隨機變量（RVs）的不確定性是概率模型。PLF的根本任務是根據給定的輸入RVs的統計信息及其多重相關性，表征結果變量（母線電壓和支路功率流）的概率分布^[3-4]。PLF評價的方法包括數值計算、近似分析方法。Monte-Carlo模擬（MCS）是PLF的一種數值計算方法，雖然計算準確，但是復雜度很高，可以作為評價PLF算法精度的一種對比算法。基于高階累積量的分析方法是一種有效的計算方法，但是對于輸入RVs的過度依賴性，是具有挑戰性的因素^[5]。

    如今，PLF的主要研究熱點是光伏發電不確定性對電力系統的影響分析，以及電動汽車充電引起的不確定性對配電系統性能的影響^[6]。文獻[7]利用聯合累積量法分析了光伏發電高穿透率對輸電系統性能的影響，PLF也適用于分析考慮光伏發電的配電系統。另一方面，PLF用于研究考慮電動汽車充電過程分析的文獻也很多。文獻[8]中，所有EV充電過程都是采用單一排隊模型來模擬的。文獻[9]中，考慮了電動汽車的每日到達時間、發車時間和行駛距離，提出了電動汽車充電模型。文獻[10]中，使用在交通管理局收集到的實時數據構建了電動汽車的充電模型，可以預測未來電動汽車充電的數量。文獻[11]中，為了避免在高峰負荷時間充電，開發了一個基于使用時間的電動汽車充電模型等，此類文獻還有很多，不再贅述。

    根據以上綜述可知，沒有文獻綜合考慮光伏發電和電動汽車充電需求的集成相關問題，沒有考慮公共充電站和小區充電站充電速度問題，對于電網穩定性的評價存在一定的片面性。對此，本文主要是針對上述兩個問題構建考慮光伏發電和電動汽車充電的PLF影響分析問題。分類考慮了插入式混合動力電動汽車（PHEV）和電池電動車（BEV）充電問題，并采用不同的排隊模型表征小區充電和公共充電站充電模型。然后，采用基于Cornish-Fisher級數的擴展累積估計方法對模型系統進行估計。

1 概率潮流模型

1.1 輸電系統

    在電力系統中，如果其由n條母線和1條分支線路構成，則其線性PLF模型為：

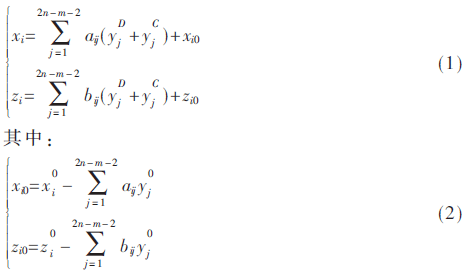
式(1)中，x、y和z分別是母線電壓、母線功率注入和線路功率流的矢量；x⁰、y⁰和z⁰分別是x、y和z的期望值；a_ij、b_ij是靈敏度系數；D和C分別代表該變量處于“離散”和“連續”狀態；x_i0、z_i0可以從確定性潮流中獲得。

1.2 徑向分布系統

1.2.1 母線電壓幅值靈敏度矩陣計算

    考慮由n個母線組成的徑向分布系統，根母線的編號為0，其余母線的編號依次為1，2，…，n-1，任意k母線的電壓幅值可表示為^[11]：

其中，|V₀|表示根母線電壓的大小；Δ|V_k|表示從根母線到第k母線的總壓降；P_i和Q_i分別為母線i上的有功和無功負載功率；R_ik和X_ik分別表示從根母線開始到母線i和母線k的供電線路的總電阻和總電抗。式(3)的緊湊形式模型可以表示為：

其中，K₁是母線電壓幅值靈敏度矩陣，負載功率P和Q為RVs。

1.2.2 支路潮流靈敏度矩陣計算

    令徑向系統有l個分支數，可通過兩步過程建立支路潮流靈敏度矩陣。首先，假設系統是無損的，無損支路潮流靈敏度矩陣K₂可利用母線負載函數進行計算。然后，支路損耗可表示為母線負荷功率函數，并可計算支路損耗靈敏度矩陣K₃。最后，最后，利用K₂和K₃的總和可獲得支路潮流的靈敏度矩陣K₄。考慮到無損耗系統，任意支路i-j(母線i與母線j相連)的有功和無功支路功率流可表示為：

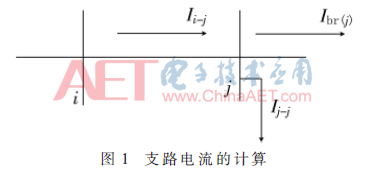
    根據式(8)~式(10)，可獲得式(7)的緊湊形式模型為：

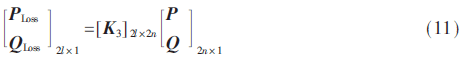
    最后，K₄可利用K₂和K₃計算得到，即K₄=K₂+K₃。

1.3 網格分布系統

    與徑向分布系統不同，在網格分布系統中無法直接獲得案例的靈敏度矩陣K₁和K₄。首先，通過在其中一個局部母線上斷開循環，可將網狀分布系統轉換為徑向分布系統。這會導致產生循環斷點(LBPs)，如圖2所示^[12]。

    圖2中，循環斷點j₁和j₂上的注入電流分別為I_ij和-I_ij，其中I_ij是環路斷開前流經母線j的電流。則可利用類似徑向分布系統的計算過程獲得矩陣K₁和K₄的計算結果。

    為了計算LBP的注入電流，可采用等效矩陣[Z_Th]方法，LBP的功率注入過程如圖3所示。下面的迭代過程可以計算獲得注入電流矢量[I_t]的元素I_tj：

    (1)構建等效矩陣[Z_Th]；

    (2)利用向前向后掃描迭代法，計算LBPs兩端的電壓降，第一次迭代的電流的初始值設定為零；

    (3)注入電流的增量計算形式為[ΔI_t]=[Z_Th]^-1[V_Th]，其中[V_Th]是LBPs兩端包含電壓降的矢量；

    (4)在任意的k步迭代中，利用下式更新LBP電流注入：[I_t]^k=[I_t]^k-1+[ΔI_t]^k。

    (5)重復執行步驟(2)~步驟(4)，直到上述計算過程收斂，收斂的閾值可設定為0.01 V。

    同時，根據圖3所示過程，令S_j為母線j上的復雜的功率需求，在創建了循環斷點j₁和j₂后，循環斷點j₁和j₂上的復雜的功率需求計算形式為：

式中，V_j1和V_j2分別為循環斷點j₁和j₂上電壓。

2 考慮光伏發電和電動汽車充電的不確定模型

2.1 光伏發電功率

    在光伏系統中，真正的光伏設備發電功率P_PV對于太陽輻照度具有較強的依賴性，但是因為氣候條件（云和霧）的不確定性，導致其模型預測存在較大困難。根據文獻[10]，光伏設備發電功率P_PV可計算為：

2.2 電動汽車功率需求

    目前，有兩種類型的電動汽車，第一種是由電池和ICE共同進行供電的PHEV，第二種是只由電池進行供電的BEV。在電動汽車充電過程中，因為每個電動車有不同的電池型號和容量，因此它們的充電過程是不同的，并具有時變特性。對于PHEV類型電動汽車，工作狀態可表示為：

其中，Z是標準高斯RV。分布參數μ_m和σ_m分別是M_D自然對數的平均值和標準偏差值，μ_m和σ_m分別與非對數平均值μ_md和標準偏差σ_md有關：

    利用排隊理論可得到BEV和PHEV的融合充電需求。對充電站建立排隊模型M/M/C，其中，第一個M表示客戶到達時間，其滿足均值時間為T_λ的指數隊列。第二個M表示均值時間為T_μ的顧客服務時間，C表示每次服務的最大客戶數。等待服務客戶數被認為是無限的。在任何時刻客戶數量為n₁概率為：

其中，U是均勻分布的RV。電動汽車需要在最小時間T_min內完成充電。此外，充電時間因為電池容量的限制不應超過最大時間T_max。BEV中不考慮最大時間問題，因為其允許完全充電。由于充電站需要快速充電，因此使用3級充電(400 V/63 A)。但是，在小區充電情況下，慢充電過程是可以接受的，可考慮1級充電過程(230 V/ 16 A)。充電電壓V和最大電流I_max是根據充電水平確定的。電動汽車的總充電需求可以計算為：

其中，I_i是第i個EV的充電電流。

3 基于Cornish-Fisher擴展累積估計

3.1 結果變量的累積量估計

    對于兩輸入情形，兩個相關聯的EVs輸入X₁和X₂，其累積量計算公式為：

3.2 結果變量的近似概率分布

    使用Cornish-Fisher級數展開法（CFM）構建結果變量的前五級近似概率分布。利用Q標準與高斯分布分位數Q(q)，構建變量Y的CFM近似結果累積概率圖，本文中選取q=1 000。結果變量Y分量可以用式(39)和式(40)進行近似：

3.3 計算過程

    為了獲得靈敏度矩陣模型的PLF，MCS和ECM的計算程序如下：

    過程1：供電系統蒙特卡洛模擬

    (1)利用多項式正態變換技術按給定的相關系數矩陣獲得相關樣本輸入RVs的合并。

    (2)采用Newton-Raphson迭代法對每一組輸入RVs樣本集進行模擬，從而獲得結果變量的樣本輸出。

    (3)結果變量的統計矩和概率分布可以從步驟(2)中獲得的樣本中建立。

    過程2：配電系統蒙特卡洛模擬

    (1)PHEVs和BEVs的瞬態充電數量，對于公共充電站利用公式（26）隨機生成，對于小區充電站利用公式（27）隨機生成。然后，對于每種情形，分別執行步驟(2)~步驟(8)。

    (2)根據公共充電站和小區充電站的市場份額選取不同的PHEVs和BEVs參數。

    (3)對于PHEVs，利用公式（18）生成P_EV和B_CAP的值。對于BEVs，令P_EV=1，則利用均值μ_CAP和方差σ_CAP的高斯分布函數隨機生成B_CAP。如果B_CAP的計算值超出限定值則將其設定為其設定值邊界值。

    (4)利用公式（20）計算EV的每英里的能量消耗M_E，利用公式（21）隨機生成EV每天行駛的英里數M_D。

    (5)對于PHEV利用公式（24）計算每輛電動車的每日充電量E_D，對于BEV，每輛電動車的每日充電量E_D=M_DM_E。

    (6)利用公式（28）隨機生成充電時間T。

    (7)對于PHEV，其中I_max和V取決于第3節所述的充電級別。

    (8)利用公式（29）計算總的充電需求。

    (9)對于給定的相關系數矩陣，輸入樣本RVs之間的相關性可采用多項式正變換技術獲得。

    (10)通過前推回代迭代法模擬每一組輸入RVS樣品獲得樣品的結果變量輸出。

    (11)對于網格系統情形，首先將系統轉換成徑向分布系統，見1.2節所述，然后執行步驟(10)。

    (12)結果變量的統計矩和概率分布可以從步驟(10)和步驟(11)獲得的樣本中建立。

    過程3：Cornish-Fisher級數擴展累積估計

    (1)計算五級累積量：①隨機生成的EV負載需求，見過程1~2；②其他輸入RVs，例如光伏發電及其配電系統的融合總線負荷功率。

    (2)計算母線電壓和支路潮流靈敏度矩陣。

    (3)利用步驟(2)和3.1節內容計算結果變量的前五級累積量輸出。

    (4)利用3.2節使用Cornish-Fisher級數展開法近似結果變量的累積概率圖。

4 實驗分析

    本節中將分別在供電和配電系統中與MCS的性能進行了比較，同時考慮方案的準確性和計算效率，驗證所提方法的有效性。

4.1 Ward Hale 6-bus供電系統測試

    Ward Hale 6-bus系統是由2個發電機組、7條供電線路和2個變壓器分支電路構成的簡單供電系統^[13-14]。集合(PV₁，PV₂)和(PV₃，PV₄)分別代表光伏發電機組1和光伏發電機組2。光伏發電機組線性化模型可利用式(15)表示。

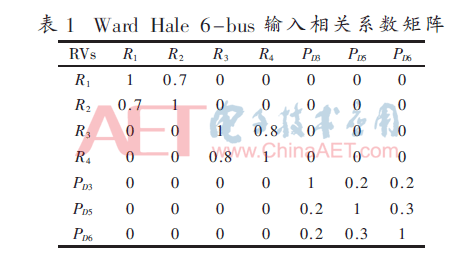
    考慮輸入RVs相關和不相關兩種情形，對于相關輸入RVs，輸入RVs相關系數保持固定。假定R₁、R₂、R₃和R₄四組RVs與T₁、T₂、T₃和T₄四組RVs之間的固定相關系數為0.3，其余的相關系數可構成矩陣形式，如表1所示。

    對于不相關輸入RVs，輸入RVs是不相關的，分別對光伏發電對結果變量的影響在基本情況下和光伏滲透情況下進行研究。絕對誤差百分比e_X作為誤差評價指標，其中e_X=(e_μ+e_σ)/2，誤差均值e_μ和方差均值e_σ的具體計算形式為：

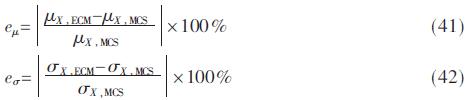
    圖4給出了系統在基本情況下（25%光伏滲透）和增加滲透后（50%光伏滲透）的概率密度累積量隨功率損耗的變化曲線。

    根據圖4實驗結果可知，在基本情況下（25%光伏滲透）和增加滲透兩種系統中，其概率密度隨功率損耗的增加而增大，但是總體上光伏滲透越小概率密度累積量越小。

    由于恒定功率因數假設，總線3、5和6的負載功率的有功和無功分量是完全相關的。因為相關系數獨立于電網規模，Q_D3、Q_D5和Q_D6的相關系數矩陣與表2設定相同。在表2中比較了考慮輸入RVs相關和不相關兩種情形下使用該模型的有效性。

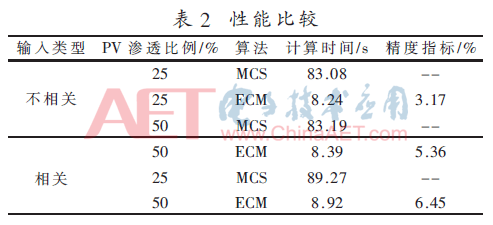
    根據表2實驗結果可知，在考慮輸入RVs相關和不相關兩種情形下，在計算時間上，本文方法相對于蒙特卡洛方法具有明顯的優勢，本文方法計算時間保持在10 s以下，而對比算法的計算時間在80 s以上。在精度指標上，因為蒙特卡洛采用的是大量選取樣本點進行模擬的方法，因此其可近似于真實值，本文將其作為參照，可見本文算法與蒙特卡洛方法在誤差上保持在7%以下，體現了較高的精度性能。

4.2 典型IEEE 140-bus配電模型測試

    本實驗采用的實驗模型如圖5所示，利用圖5所示IEEE 140-bus配電模型^[15]，結合本文所提出的概率潮流計算模型進行實驗分析，對比算法選取本文算法、三點估計和蒙特卡洛三種方法。

    圖5所示的配電模型的總負荷是26.33+j18.61MV·A；該配電模型的電源點有三個，分別位于標號136、123和107位置處，其注入功率分別是6+j3.5MV·A，4+j2.5MV·A和7+j4.5MV·A。配電模型的饋線電阻是r=0.27 Ω/km，饋線電抗是x=0.327 Ω/km。

    這里以南京市玄武區2006年到2016年共10年間的氣候監測數據作為模擬數據參數。以2013年為例，選取四個具有季節特點的日期的檢測數據，時間點分別是1月15日，4月22日，8月9日，11月18日，分別位于春夏秋冬四個季節中，具體信息見表3所示。

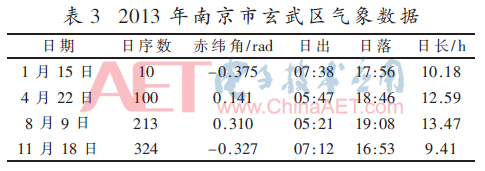
    表3中，給出了南京市玄武區2013年一年中選取的四個時間節點的赤緯角、日序數、日出日落兩個標志性事件的時間。IEEE 140-bus配電模型的發電設備位于節點99位置處，該配電模型的峰瓦值參數取值是16 MW；該配電模型的覆蓋區域內的PHEVs和BEVs的數量分別是2 900臺和600臺。電動汽車進行充電的節點位置是137節點處和113節點處，分別是住宅區的慢充節點和公共區域的快充節點，電動汽車在進行充放電過程中的功率是3.7 kW，這個過程中的能量轉換率是0.80，功率因子參數的取值是0.98。圖6~圖7是采用三點估計法、本文算法和蒙特卡洛模擬方法獲得的1月15日10：00~11：00時間段內126節點和52節點的有功功率和電壓幅值兩個參數的概率密度。在上述選取的四個時間點上，本文方法和三點估計方法與蒙特卡洛方法相比在126節點和節點52的有功功率和電壓幅值的模擬誤差以及計算時間對比情況見表4結果所示。

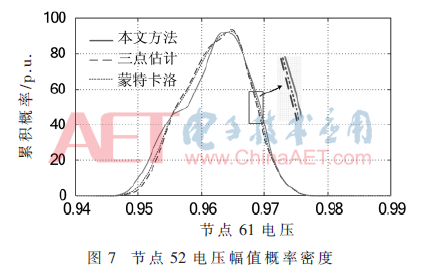
    分析上述圖6~圖7所示的有功功率和電壓幅值兩個參數的概率密度取值情況，本文方法與蒙特卡洛方法獲得的線路126和節點52的有功功率和電壓幅值兩個參數的概率密度的偏差控制在5%以內，而采用三點估計方法獲得的線路126和節點52的有功功率和電壓幅值兩個參數的概率密度的偏差在10%以內。

5 結論

    現代社會中，隨著經濟和科技的快速發展，新能源技術快速發展和應用，針對這種發展背景，本文研究了考慮包含光伏發電和電動汽車充電的電力系統模型設計問題。特別是，光伏發電和電動汽車充電過程中存在的不確定性、時變性，通過理論分析得到了其概率潮流計算模型，并采用不同的排隊模型表征小區充電和公共充電站充電模型。然后，采用基于Cornish-Fisher級數的擴展累積估計方法對模型系統進行估計，實現了估計模型的降階處理，提高了計算效率。實驗結果顯示，所提方法具有相對更高的計算精度和計算效率。

參考文獻

[1] Dong Fugui，Zhang Wen.Evaluation and comparison of power network plans including distributed photovoltaic generations[J].Operational Research，2017，17(3)：885-900.

[2] LING J M，LIU P H.The performance analysis of photo-voltaic generation using the improved incremental conductance method under varying solar irradiance[J].Microsystem Technologies，2018，24(1)：235-241.

[3] 楊曉東，張有兵，蔣楊昌，等.微電網下考慮分布式電源消納的電動汽車互動響應控制策略[J].電工技術學報，2018，33(2)：390-400.

[4] JANIK P，KOSOBUDZKI G，SCHWARZ H.Influence of increasing numbers of RE-inverters on the power quality in the distribution grids：a PQ case study of a representative wind turbine and photovoltaic system[J].Frontiers in Energy，2017，11(2)：155-167.

[5] Chen Weidong，Song Huan.Optimal subsidies for distributed photovoltaic generation: maximizing net policy benefits[J].Mitigation and Adaptation Strategies for Global Change，2017，22(3)：503-518.

[6] Dang Hongmei，SINGH V P，GUDURU S，et al.Nanotube photovoltaic configuration for enhancement of carrier generation and collection[J].Nano Research，2015，8(10)：3186-3196.

[7] DAUD M Z，MOHAMED A，HANNAN M A.A novel coordinated control strategy considering power smoothing for a hybrid photovoltaic/battery energy storage system[J].Journal of Central South University，2016，23(2)：394-404.

[8] 馬益平.考慮電動汽車調度的微電網混合儲能容量優化配置[J].電力系統保護與控制，2017，45(23)：98-107.

[9] Wang Zhongkui，PASSINO K M，Wang Jin.Optimal reactive power allocation in large-scale grid-connected photovoltaic systems[J].Journal of Optimization Theory and Applications，2015，167(2)：761-779.

[10] Qi Liqiang，Zhang Yajuan.Effects of solar photovoltaic technology on the environment in China[J].Environmental Science and Pollution Research，2017，24(28)：22133-22142.

[11] 徐從啟，高瑞林，賈桂芝，等.考慮分時電價電動汽車負荷的微電網優化調度[J].電氣工程學報，2017，12(11)：12-20.

[12] CORONA B，ESCUDERO L，QUEMERE G，et al.Energy and environmental life cycle assessment of a high concentration photovoltaic power plant in Morocco[J].The International Journal of Life Cycle Assessment，2017，22(3)：364-373.

[13] KHAN M J，MATHEW L.Different kinds of maximum power point tracking control method for photovoltaic systems：a review[J].Archives of Computational Methods in Engineering，2017，24(4)：855-867.

[14] PACHECO-TORRES R，LOPEZ-ALONSO M，MARTINEZ G，et al.Efficient design of residential buildings geometry to optimize photovoltaic energy generation and energy demand in a warm Mediterranean climate[J].Energy Efficiency，2015，8(1)：65-84.

[15] Wang Jianjun，Chen Shanben，Shao Yufeng.Research on maximum power point tracking in redundant load mode for photovoltaic system[J].Journal of Shanghai Jiaotong University (Science)，2016，21(3)：257-262.

作者信息:

劉媛媛

（南京大學 新能源學院，江蘇 南京210000）