崔翔鵬，黃洪瓊

　　（上海海事大學 信息工程學院，上海 201306）

　　摘要：為了提高船舶交通流預測的效率和準確率，分析了船舶流量預測中的影響因素多、非線性、隨機性等問題，建立了ELM(極限學習機)預測模型。同時為了避免極限學習機算法受輸入權值矩陣和隱含層偏差隨機性的影響,算法又采用GA(遺傳算法)對極限學習機的輸入權值矩陣和隱含層偏差進行優化,建立GAELM船舶交通流預測模型。利用上海洋山港船舶流量對該模型進行了實例分析，通過MATLAB仿真進行預測，將GAELM模型與單純的BP模型、ELM模型進行對比和分析，結果表明：GA-ELM模型具有更高的預測精度和效率，從而能夠相對準確、高效地對船舶交通流量進行預測。

　　關鍵詞：船舶交通流量；遺傳算法；極限學習機；預測

　　中圖分類號：TP391.9文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.09.005

　　引用格式：崔翔鵬，黃洪瓊.基于GA優化ELM的船舶交通流預測模型［J］.微型機與應用，2017,36（9）：15-17，21.

0引言

　　近年來，隨著社會經濟和對外貿易的迅速發展，各種水域的船舶流量不斷增加，導致了航行水域的船舶交通事故頻發，不僅帶來了巨大的經濟損失更是造成了人員傷亡。因此，提升航行水域船舶流量預測的準確性和高效性尤為重要。同時，預測的準確性和高效性又為航道的規劃設計和船舶通航管理提供了有力的依據。目前國內外研究船舶流量預測的方法有支持向量機預測［1］、回歸分析［2］、灰色分析［3］等方法，然而這些預測方法都很難滿足預測的高效性和準確性。

　　針對現有預測方法存在的泛化能力不強、訓練速度慢、預測準確率不高等不足之處，本文采用了一種新的船舶交通流量預測模型，即GA-ELM預測模型，首次將遺傳算法(GA)對極限學習機(ELM)進行優化的方法用于船舶交通流量預測。遺傳算法具有良好的隨機搜索能力，它是根據生物界的進化規律演化而來；而極限學習機(ELM)算法具有獲得唯一最優解以及學習速度快、泛化性能好等優點。將兩者結合，利用GA優化ELM的輸入層與隱含層間的連接權值及隱含層神經元的閾值，實現了預測船舶交通流量的目的。

1極限學習機(ELM)

　　南洋理工大學副教授黃廣斌于2004年提出極限學習機(Extreme Learning Machine，ELM)算法，ELM是一種改進的前饋神經網絡(SLFN)學習算法，相比于傳統

　　的SLFN，ELM具有訓練速度快、獲得全局唯一的最優解且具有良好的泛化能力［4］。另外，在樣本數據不足的情況下，ELM的預測結果也較好，其結構如圖1所示，由輸入層、隱含層和輸出層三部分組成。

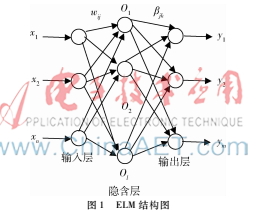
　　通常設wij(i=1,…,l,j=1,…,n)為輸入層和隱含層之間的連接權值；bk(k=1,…,l)為隱含層神經元的閾值；βjk(j=1,…,l,k=1,…,m)為隱含層和輸出層之間的連接權值；wij表示輸入層第i個神經元和隱含層第j個神經元的連接權值；βjk表示隱含層第j個神經元與輸出層第k個神經元的連接權值。設訓練集輸入矩陣X和輸出矩陣Y分別為

　　X=［x1,x2,…,xn］T，Y=［y1,y2,…,ym］T(1)

　　設隱含層神經元的激勵函數為Sigmoid，其表達式為：

　　式中，j=1,2,…,n；

　　wi=［wi1wi2…wim］。則式(4)可以表示為Hβ=T′，式中，T′為T的轉置矩陣。神經網絡隱含層的矩陣H為:

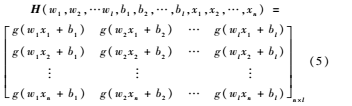
　　當隱含層的神經元數目等于訓練集樣本數目時，設定w和b，單隱層前饋神經網絡(Singlehidden Layer Feedforward Neural Network,SLFNN)能夠沒有誤差接近訓練樣本［5］，即:

　　式中，j=1,2,…,m。然而當訓練集X的樣本數較多時，通常取隱含層神經元的個數K<n，SLFN的訓練誤差可以任意逼近［5］ε>0，即：

　　當選定激勵函數g(x)可以無限可微時，取w和b，β值可以通過式(8)求得最小二乘解，即：

　　minβHβ－T′(8)

　　解得:

　　β=H+T′(9)

　　其中，H+為隱含層輸出矩陣H的MoorePenrose逆。

　　2GA-ELM預測模型的建立

　　遺傳優化算法是根據生物界的進化規律演化而來的隨機化搜索方法，在內在的隱并行性、實用性和全局尋優能力等方面具有較大優勢。

　　由于ELM模型隱含層輸入權值和偏差是隨機給定的，可能存在某些隨機設定值為0時，導致部分隱含層節點失效。因此本文采用遺傳算法對輸入權值和偏差進行優化，其通過遺傳算法的選擇、交叉、變異操作得到最優的初始權值和閾值，進而得到最優的ELM模型。圖2為GA-ELM模型的流程圖，訓練步驟如下:

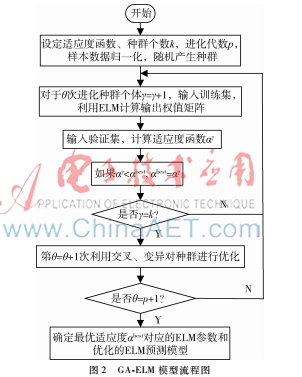
　　(1)設定適應度函數、種群個數k及進化次數p,本文選取測試集樣本數據均方差作為適應度函數。適應度函數值越小，模型越精確。

　　(2)規定種群。種群個數k一般設定為20~40個。個體的長度是由隱含層輸入權值矩陣和偏差向量構成，即D=L(n+1)，其中L為隱含層節點數量，n為輸入層神經元數量，即輸入向量的維度。

　　Qγ=［aγ11,aγ12,…,aγ1L,aγ21,aγ22,…,aγ2L,…aγL1,aγL2,…，aγLL,bγ1,bγ2,…,bγL］，其中Qγ表示種群中第γ個個體，1≤γ≤k，aij、bj在區間［-1，1］隨機取值。

　　(3)局部求解最優適應度函數αbest。αbest初始值為

　　10，θ及γ的初始值為0，把訓練數據歸一化后帶入模型，依次求出每個個體的適應度函數，直到γ=k時循環終止，解得αbest的值［6］。

　　(4)全局求解最優適應度函數αbest。每次解得最優適應度函數后，采用交叉、變異將種群進行優化，檢驗進化代數θ，當θ小于等于p時，將γ值初始為0，退回到步驟（3），直到θ大于p停止運算，即得出的αbest為最優適應度函數，根據所對應的參數便可得到優化的ELM模型。

3實驗仿真及分析

　　3.1實驗數據及設置

　　以上海洋山深水港經過的船舶為研究對象，根據上海洋山港統計的數據，選取2016年4月10日至2016年7月16日的船舶流量數據作為預測數據。前60天數據作為預測數據，后37天數據作為測試數據。選取自然因素、船舶平均噸位、物流成本、業務指數、上海經濟指數5個因素來建立預測模型。為降低預測誤差，對樣本數據按式(10)歸一化處理［7］。

　　仿真實驗時，利用MATLAB中的Sheffield工具箱實現GA，構建最佳的GAELM船舶流量預測模型。設定GA的參數如下：種群大小為20，最大遺傳代數為100，交叉概率0.75，變異概率0.02，代溝0.95。

　　3.2實驗仿真效果及分析

　　為了對實驗的效果進行比較，本文分別記錄BP、ELM和GAELM 3種算法的MAE、MAPE、RMSE和仿真時間。令pt為實際測量值，預測值為t，n為觀測序列總數，預測指標如下［8］:

　　將這3種模型進行性能比較，其結果如表1所示。此外，對BP神經網絡、ELM模型和GAELM模型分別進行了仿真實驗和對比，仿真結果如圖3~圖5所示。

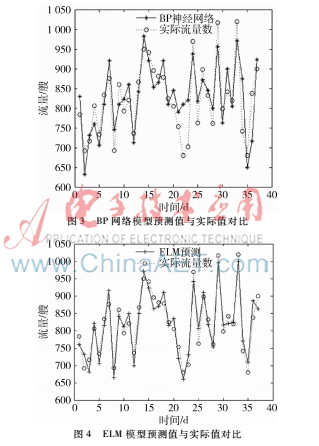
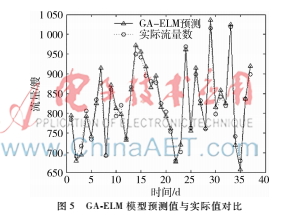
　　從表1及圖3~圖5可見，BP神經網絡和ELM模型都得到了相應的預測效果，但在預測的準確性上不及GA_ELM模型。由于BP神經網絡對樣本數存在較高的要求，會存在過擬合現象以及ELM中隨機賦值問題，導致這兩種算法預測的準確性受到了影響。GA具有更好的全局尋優能力，采用GA優化ELM模型的隨機賦值問題，使其得到最優解，得到的預測誤差變小。

　　由表1可見，GA-ELM預測模型的平均絕對誤差、平均絕對百分誤差、均方根誤差和仿真時間都明顯小于BP模型和ELM模型。因此，GA-ELM模型比BP模型以及ELM模型在預測的準確性和高效性等方面具有更好的優勢。

4結論

　　本文首次將遺傳算法優化的極限學習機模型應用于船舶流量預測中，根據GA算法原理，對ELM預測模型的參數的選擇進行優化，避免隨機性對模型預測的準確性的影響，提高了預測精度。

　　利用GA-ELM對船舶交通流量進行預測，將預測效果與BP模型和ELM模型進行對比分析。結果表明，GA-ELM具有更好的泛化能力和良好的穩定性，預測結果與實際船舶交通流量相吻合，可以準確、高效地預測船舶交通流量，為船舶交通流量的預測提供了一種新方法。

參考文獻

　　［1］ 馮宏祥,肖英杰,孔凡邨.基于支持向量機的船舶交通流量預測模型［J］.中國航海,2011,34(4):62-66.

　　［2］ 王東, 熊錫龍. 基于影響因素分析的船舶交通流量預測多元線性回歸模型［J］. 船海工程, 2010, 39(3):178-180.

　　［3］ 李俊, 徐志京, 唐貝貝. 基于GA優化的灰色神經網絡船舶交通流量預測方法研究［J］. 船海工程, 2013, 42(5):135-137.

　　［4］ HUANG G B, ZHU Q Y,SIEW C K. Extreme learning machine: theory and applications［J］. Neurocomputing, 2006, 70(13):489-501.

　　［5］ HUANG G B, ZHU Q Y,SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks［J］. Proceedings of International Joint Conference on Neural Networks, 2004, 2(2):985-990.

　　［6］ 王新民, 李天正, 張欽禮. 基于 GA-ELM 漿體管道輸送臨界流速預測模型研究［J］. 中國安全生產科學技術, 2015(8):101-105.

　　［7］ 鈕浩東, 黃洪瓊. 基于FOA優化GRNN的船舶交通流預測模型［J］. 微型機與應用, 2016, 35(12):81-83.

　　［8］ 郎茂祥. 預測理論與方法［M］. 北京：清華大學出版社, 2011.