0 引言

    近年來，以正交頻分復用(Orthogonal Frequency Division Multiplexing, OFDM)技術為代表的多載波數據傳輸技術以其在頻譜效率、對抗多徑衰落、低的實現復雜度等方面的優異性能得到了廣泛的應用^[1-2]。然而，OFDM子載波濾波器的旁瓣電平較大，高達-13 dB，難以具備良好的頻率選擇特性，OFDM系統通過在信號前端加入循環前綴使傳輸速率降低來克服此缺陷。另外，OFDM系統要求相鄰子載波之間嚴格滿足正交性。而濾波器組多載波系統(Filter Bank-based MultiCarrier，FBMC)只需通過設計良好頻率選擇特性原型濾波器即可，不需要在信號前端加入循環前綴和相鄰子載波之間的正交性，提高了信號的傳輸速率和系統設計靈活性^[3-5]。因此，目前將要代替OFDM技術逐漸被公認是基于濾波器組的多載波技術^[6-7]。

    在FBMC技術中，發送端通過合成濾波器組來實現多載波調制，接收端通過分析濾波器組來實現多載波解調。這些濾波器組由原型濾波器經調制得到^[8-11]。其中，原型濾波器的設計是核心問題，現有的設計算法中，一類是將濾波器組的設計問題轉化為以結構參數為變量的優化問題，主要有頻率采樣的方法^[12-16]、窗函數方法^[17]。其中，窗函數方法是通過對理想濾波器加窗來構造原型濾波器，從而將設計問題轉化為關于窗函數參數的優化問題。頻率采樣方法是通過對理想濾波器頻率響應進行等間隔采樣，然后求逆傅里葉變換，得到原型濾波器的沖激響應函數。這類方法設計簡單，可調節部分參數，設計的原型濾波器具有閉合解，但是因設計自由度小導致性能受限。另一類方法是直接對原型濾波器的系數進行優化，其中代表性算法是基于半定規劃(SDP)的方法^[18]。將原型濾波器的設計問題被歸結為一個帶約束優化問題，從而能獲得更佳的原型濾波器。但是所歸結的優化問題是關于濾波器系數的高度非線性優化問題，求解較為困難。為了克服這些缺點，文獻[19]采用基于?琢BB(?琢-based Branch and Bound)來極大地降低直接算法的求解規模。該算法通過對約束進行有效近似，從而極大地降低了優化變量個數。但是，所需優化的變量個數通過求解SQP來確定,導致計算復雜度高^[19]。該方法設計所得的原型濾波器具備高阻帶水平和較低的失真。但是該方法近似中舍去了大量的設計自由度，導致原型濾波器設計性能受限。

    本文所考慮的設計是快速優化得到原型濾波器，根據FBMC系統的性能指標，將原型濾波器的設計問題歸結為一個無約束的優化問題，其目標函數是由FBMC系統的符號間干擾(ISI)、信道間干擾(ICI)和原型濾波器的阻帶能量所導出，運用修正的牛頓迭代法，可以快速設計得到原型濾波器。與已有設計算法進行仿真對比發現，本算法具有更低的計算代價，得到的FBMC系統有著較好系統性能，從而可以快速而有效地設計大規模通道的FBMC系統。

1 FBMC系統的基本結構

    不失一般性，本文將以FBMC-OQAM(Offset Quadrature Amplitude Modulation)系統為例來闡述FBMC系統的設計問題。圖1給出了FBMC-OQAM系統的模型，其中a_k(n)，b_k(n)是第k通道上第n個輸入信號的實部和虛部，則輸入信號x_k(n)=a_k(n)+jb_k(n)。偏移正交振幅調制(OQAM)中，實部與虛部在時域T/2處同相交錯的相互正交，其中T是傳輸信號的周期，N是綜合濾波器通道數，每個通道之間的載波頻率是1/T。FBMC-OQAM的基帶輸入信號為^[7]：

2 FBMC系統的設計

2.1 FBMC系統中性能指標

    在系統中，可以通過減小ISI/ICI來提高系統性能，從而使得系統滿足近似完全重構條件，而ISI/ICI可以被確定通過原型濾波器的設計^[19]。根據文獻[19]表明ISI/ICI的整體水平可以被表示為：

    將式(7)和式(8)寫成矩陣相乘的形式：

2.2 原型濾波器的設計

    基于上述的分析，可以將原型濾波器的設計問題歸結為無約束的優化問題，然后用修正牛頓算法進行求解該優化問題。在FBMC-OQAM通信系統中，原型濾波器需要滿足線性相位結構^[20]，即：

    另外，為使原型濾波器具有好的頻率特性，期望原型濾波器具備高的阻帶衰減，這可以通過控制其阻帶能量來達到：

    (3)判斷||d_k||₂≤η(η是給定的很小的正數)是否成立，若成立，終止該算法迭代，x_k+1為最優的結果；若不成立，令x_k=x_k+1，k=k+1并返回到步驟(2)繼續迭代。

2.3 計算復雜度分析

    本文通過修正牛頓迭代算法來設計一個綜合性能較好的FBMC-OQAM系統，原型濾波器都是通過閉合公式求解，計算復雜度來自求解線性等式(28)，主要有求矩陣B(x_k)的逆，以及計算向量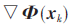和矩陣B(x_k)。另外，如果搜索步長取最優值，則計算復雜度高^[20]，所以式(29)采用了單位步長進行計算。因此本文算法有較小的計算消耗。此算法適用于大規模FBMC-OQAM系統的設計，為未來5G通信中發揮作用提供了設計算法方面的儲備。

3 仿真結果與分析

    對于FBMC-OQAM系統的評價指標，采用與文獻[20]相同的評價指標：最小均方誤差(MSE)和阻帶能量(SE)。設計例子的仿真程序使用的是MATLAB2010b軟件編程并運行于Intel i3-M380主頻2.53 GHz的PC。

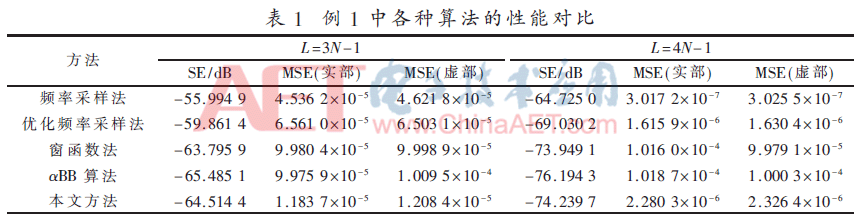
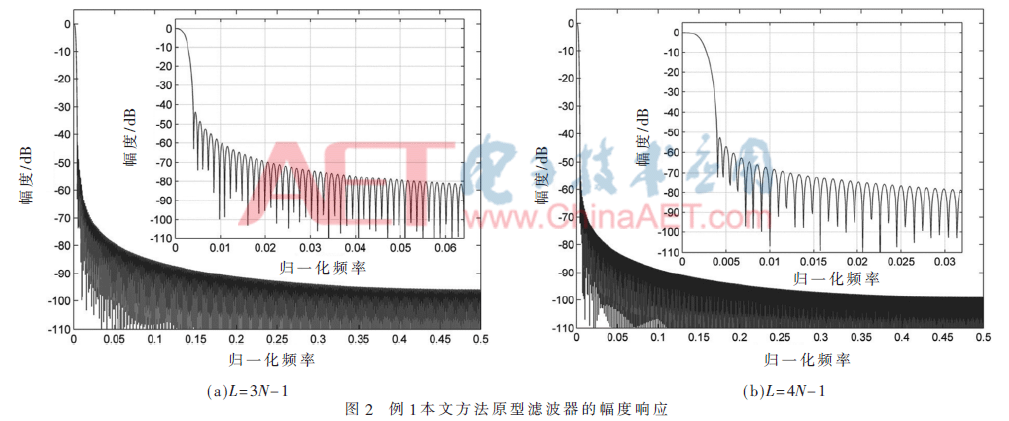
    例1：設計一個通道載波為N=256、原型濾波器長度L=3N-1和L=4N-1的FBMC-OQAM系統。此外，頻率采樣法^[13]、優化頻率采樣法^[15]、窗函數法^[17]和αBB算法^[19]，在本文設計方法中設定η=1×10^-5和α=0.1，在L=3N-1和L=4N-1情況下，本文設計算法迭代3次便可達到終止條件，CPU運行時間24 s(L=3N-1)和60 s(L=4N-1)，表1給出了5種方法所得到的FBMC-OQAM系統性能對比，并且得到的原型濾波器的幅度響應如圖2所示。從表1中可以看出本文設計方法提高了FBMC-OQAM系統整體性能，與文獻[19]中的αBB算法相比，本文設計方法損耗較小阻帶能量來得到更加小的MSE，并且當L=4N-1、α=0.1時計算花費的時間(60 s)遠遠小于αBB算法計算時間(1 803 s)；與其他方法比較，本文方法通過控制權值，可以更加靈活地平衡系統ISI/ICI與阻帶能量之間的關系，從而得到整體性能更加良好的FBMC-OQAM系統。

    例2：設計一個大規模通道載波FBMC-OQAM系統，其中：載波通道為1 024，原型濾波器長度L=3N-1，α=0.1，表2給出所得FBMC-OQAM系統性能，同時原型濾波器的幅度響應如圖3所示。

4 結束語

    本文圍繞如何有效地設計FBMC-OQAM系統的原型濾波器問題，提出了一種基于無約束優化的快速算法，優化的目標函數綜合考慮FBMC-OQAM系統的ISI/ICI和阻帶能量。基于推導出的目標函數的梯度向量和海森矩陣，采用修正牛頓算法快速有效地求解了該優化問題。原型濾波器的迭代更新有閉合解，該方法計算復雜度低，適用于大規模系統的設計。理論分析和仿真結果聯合表明，本文方法設計得到的FBMC-OQAM系統相比于現有方法有著更好的整體性能。

參考文獻

[1] FARHANG B B.OFDM versus filter bank multicarrier：development of broadband communication systems[J].IEEE Signal Process. Mag.2011，28(3)：92-112.

[2] NEE R V，PRASAD R.OFDM for wireless multimedia communications[M].OFDM for Wireless Multimedia Communications.Artech House，2000.

[3] VAIDYANATHAN P P.Filter banks in digital communications[J].IEEE Circuits and Systems Mag，2001，1(2)：4-25.

[4] SIOHAN P，SILCLET C，LACAILLE N.Analysis and design of OFDM/OQAM systems based on filter bank theory[J].IEEE Trans.Signal Processing，2002，50(5)：1170-1283.

[5] AMINI P，KEMPTER R，FARHANG B B.A comparison of alternative filter bank multicarrier methods for cognitive radio systems[C].Presented at the Softw.Defined Radio Tech.Conf..Orlando：FL，2006：13-16.

[6] FARHANG A，MARCHETTI N，DOYLE L E，et al.Filter bank multicarrier for massive MIMO[C].Vehicular Technology Conference.IEEE，2014：284-7.

[7] BANELLI P，BUZZI S，COLAVOLPE G，et al.Modulation formats and waveforms for 5G networks：who will be the heir of OFDM?：an overview of alternative modulation schemes for improved spectral efficiency[J].IEEE Signal Process.Mag，2014，31(6)：80-93.

[8] PHOONG S M，CHANG Y B，CHEN C Y.DFT-modulated filterbank transceivers for multipath fading channels[J].IEEE Trans.Signal Process，2005，53(1)：182-192.

[9] CVETKOVIC Z.Tight Weyl-Heisenberg frames in l2(Z)[J].IEEE Trans.Signal Process，1998，46(5)：1256-1259.

[10] BEAULIEU F D，CHAMPAGNE B.Multicarrier modulation using perfect reconstruction DFT filter bank transceivers[C].In Proc.5th Int.Conf.Inf.，Commun.，Signal Process.，Bangkok，Thailand，2005：111-115.

[11] BEAULIEU F D.Multicarrier transceiver using DFT filter banks with perfect reconstruction[D].Thesis，McGill University，2007.

[12] BELLANGER M G.Specification and design of a prototype filter for filter bank based multicarrier transmission[C].In Proc.IEEE Int.Conf.Acoust.，Speech，Signal Process.，Salt Lake City，UT，May 7-11，2001：2417-2420.

[13] MIRABBASI S，MARTIN K.Overlapped complex-modulated transmultiplexer filters with simplified design and superior stopbands[J].IEEE Trans.Circuits Syst.II，Analog Digit.Signal Process，2003，50(8)：456-469.

[14] CRUZ-ROLDAN F，HENEGHAN C，SAEZ-LANDETE J，et al.Multi-objective optimisation technique to design digital filters for modulated multi-rate systems[J].Electron.Lett，2008，44(13)：827-828.

[15] VIHOLAINEN A，BELLANGER M，HUCHARD M.Prototype filter design for filter bank based multicarrier transmission[C].In Prof.17th Eur.Signal Process.Conf.，Glasgow，Scotland，2009，Aug.24-28：1359-1363.

[16] VIHOLAINEN A，BELLANGER M，HUCHARD M.Prototype filter and structure optimization[OL].[2016-10-05].Available：http：//www.ict-phydyas.org/delivrables/ PHYDYAS-D5-1.pdf/view.

[17] MARTIN P，Bregovic R，MARTIN M A，et al.A generalized window approach for designing transmultiplexers[J].IEEE Trans.Circuits Syst.I，Reg.Papers，2008，55(9)：2696-2706.

[18] CHEN D，QU D M，JIANG T.Novel prototype filter design for FBMC based cognitive radio systems through direct optimization of filter coefficients[C].Wireless Communications and Signal Processing，2010 International Conference on.IEEE，2010：1-6.

[19] CHEN D，QU D M，JIANG T，et al.Prototype filter optimization to minimize stopband energy with NPR constraint for filter bank multicarrier modulation systems[J].IEEE Trans.Signal Process，2013，61(1)：159-169.

[20] JIANG J Z，SHUI P L，ZHANG Z J.Design of oversampled DFT modulated filter banks via modified Newton′s method[J].IET Signal Processing，2011，5(3)：271-280.

[21] SUN W Y，YUAN Y X.Optimization theory and methods：nonlinear programming[M].Springer Science+Business Media，Inc.，2006：203-456.

作者信息:

穆亞起

(桂林電子科技大學 信息與通信工程學院，廣西 桂林541004)