0 引言
    目前,由于煤礦盜采具有隱蔽性強、不易被發現的特點，煤礦監管部門迫切需要有一套檢測精度高、檢測周期短的監測設備來對地下巷道進行實時監測和定位。微地震監測是目前礦區防盜采中最精確、最及時、信息最豐富的監測手段之一[1]。微地震監測技術最主要的任務就是確定震源的位置[2]。而微震監測系統中的拾震器陣列的空間布置是微震監測系統能否有效并可靠運行的關鍵。國內外關于震源定位技術中拾震器陣列的空間布置對系統精度和可靠性的影響及其優化的研究的相關文獻都非常少[3，4]，因此，非常有必要對微震監測中拾震器陣列的空間布置進行研究[5]。本文提出利用神經網絡遺傳算法和微變網格射線追蹤正演模擬方法在微震定位系統中進行拾震器布陣研究來為微震監測系統選出科學合理的拾震器布陣方案。
1 微震波震源定位正反演方法和布陣方案設計
1.1 PSO-BP震源定位反演
    實際上求解震源定位問題就是解非線性方程組的問題，本文通過PSO-BP算法求解，利用PSO算法進行BP網絡參數的優化，不僅避免了BP網絡原有算法在訓練時易陷入局部極小的問題，而且提高了BP網絡的訓練速成度。所謂參數的優化，就是尋找最優的BP網絡的網絡權值和閾值，使得BP網絡的全局誤差最小化，從而尋找震源位置。
    PSO-BP 混合算法具體步驟如下：
    (1)創建三層BP網絡,構造BP網絡的輸入層、隱含層和輸出層，并隨機產生N組連接權值和閾值分布作為PSO算法的初始種群，評價每個微粒的適應度。
    (2)對每個微粒，將其適應度值與其經過的最好位置p_best作比較，如果較好，則將其作為當前的最好位置p_best。
    (3)對每個微粒，將其當前的最好位置p_best與當前整個群體中所有微粒發現的最好位置g_best作比較，如果較好，則將其作為當前群體的最好位置g_best。
    (4)用PSO公式(1)、(2)進行粒子的速度和位移的更新：
    v_i(n+1)=w·v_i(n)+c₁·r₁(p_i-x_i(n))+c₂·r₂(p_g-x_i(n))                  (1)
    x_i(n+1)=x_i(n)+v_i(n)                                                           (2)
    (5)用種群最優位置gbest更新BP網絡的權值和閾值，PSO運行結束。迭代終止條件根據具體問題選為最大迭代次數或(和)粒子群迄今為止搜索到的最優位置滿足預定目標最小適應閾值。
    (6)BP算法利用權值和閥值等網絡參數震源位置進行計算。
1.2 微變網格射線追蹤正演模擬
    射線理論正演能夠實現選擇最佳的微震波在介質中的運動軌跡[6]，因此它是進行層析反演的理論基礎,本文采用射線追蹤理論正演模擬計算。
    本文結合射線追蹤方法中的試射法和微變網格法，建立復雜介質模型以進行微震正演模擬。真實的地質情況是紛繁復雜的，對于這種界面變化復雜并且速度梯度變化較劇烈的模型，可通過將復雜介質模型離散化成小網格，應用微變網格法進行射線追蹤的方法來求解。
    結合微震監測作業特點，建立復雜介質模型：
    (1)首先建立初始模型，輸入檢波器陣列和微震源位置坐標，等間距網格化介質模型，結合模型特點設定出射角范圍。
    (2)從微震源點所在網格出發，將各網格端點作為出射角,追蹤各網格出射邊，得出交點位置。
    (3)進行網格入射邊微擾動，獲得下個網格，如此反復，直到監測井與射線相交。同網格時進入步驟(4)；否則再次劃分原區間，轉入步驟(3)。
    (4)判斷監測點與監測井交點位置的關系，符合微震精度則轉入步驟(7)；否則重新設定區間，并利用二分法劃分區間，轉入步驟(2)。
    (5)記錄射線路徑及出射角，計算射線旅行時并記錄輸出。
    假定微震波在介質離散化單元內進行傳播，已知離散化單元的位置、慢度和慢度梯度以及在射線入射口位置和此點方向，此問題可歸結為求取其出口點位置和方向。其數學描述為：非均勻介質模型，假設介質離散化單元內波速梯度為微常量，程函方程為：

1.3 布陣方案
    目前，微震監測技術在震監測傳感器布陣的可行性方面一直是一個難題。本文設計了幾種布陣方案，如圖1。為提高震源定位精度，合理布陣，并合理放置適量的拾震器，使用MATLAB編程工具實現對震源點的反演定位。用軟件計算出震源點的定位誤差并繪制出其坐標誤差圖，比較呈十字形狀、米字形狀、四邊形狀、八邊形狀的傳感器布陣方案的震源定位誤差圖，觀察其震源定位精度，選出更合理的拾震器布陣方案，實現對微震監測中拾震器布陣的評估。

圖1  4種拾震器布陣圖

2 計算機數值模擬實驗及分析
2.1 建立復雜介質數學模型
    設Rj和Si分別表示拾震器和微震源，S_i(x，y，z)為第i個微震源的實際空間坐標，R_j(x，y，z)為第j個檢波器監測點空間坐標。微震監測方式選擇井地聯合監測[7]，采用復雜介質模型，復雜地質模型為1 km×1 km×1 km 的立方體，如圖2所示。

圖2  三維復雜地質模型

    該三維模型由兩層均勻介質與一層非均勻介質組成，其中第一個界面為傾斜界面R1，第二個界面為水平界面R2：z=-800 m，其空間位置滿足關系14x-14y-5z=1 000；在這兩個界面之間嵌有一橢球體E，中心位于模型中心(0.5 km，0.5 km，-0.5 km)，其形狀滿足橢球面方程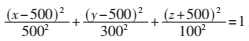：。第一層界面以上的介質I的縱波速度vp、橫波速度vs分別為2 km/s和1.2 km/s，除橢球體之外兩個界面之間介質II的地震波速度分布為：
    v_p(x，y，z)=
    2 500+0.2(x-500)+0.1(y-500)-0.6(z+500)   m/s(7)
    v_s(x，y，z)=
    1 500+0.1(x-500)+0.05(y-500)-0.3(z+500)  m/s(8)
    第二界面以下介質III為均勻介質，其速度為：v_p=3.5 km/s，v_s=2.1 km/s；橢球體內的介質速度為：v_p=3 km/s；v_s=1.7 km/s。震源位于(56 m，80 m，-20 m)。對三維介質模型，3個方向上均以10 m的間隔將模型剖分成100×100×100個立方體單元。在微機上利用微變網格射線追蹤算法計算初至波走時。
2.2 正演模擬
    在復雜介質模型中，采用微變網格射線路徑追蹤算法進行正演模擬，輸出微震波射線追蹤路徑，計算震源點至各檢波器的準確初至到時，即各檢波器到時差序列△t_i。表1給出了各種布陣方案中震源點至各檢波器到時差序列結果(以第一道檢波器到時為基準[8])。

2.3 加入隨機噪聲擾動的PSO-BP反演
    檢波器檢波時受到噪聲的干擾，這些干擾波無法過濾得十分干凈，從而引入了時間誤差，因此定位誤差是由時間誤差而來的。由于這種時間誤差是隨機的，用隨機時間擾動產生模擬定位擾動，用其估計定位誤差，進而估計和比較各種布陣方式的定位精度。本文采用正態分布作為模擬隨機噪音分布的函數形式。其中模擬過程中擾動次數要盡可能多，而在在這個模型試驗中發現，擾動150次后誤差不再繼續減小。因此，采用標準偏差為1 ms的隨機正態分布模擬時間擾動，噪聲擾動150次后加在走時上進行反演。
    反演中目標函數為非線性回歸模型(走時方程)：
   

    由拾震器坐標(Xi，Yi，Zi)得到待估計的未知參數(X₀，Y₀，Z₀，V_p，T₀)，使N個走時方程殘差平方和達到最小。
    通過微變網格射線追蹤正演程序得出了各檢波器監測點理論上的到時差序列，將它們構成學習樣本，進而進行PSO算法，從而優化BP神經網絡；在優化后得出的最優權值和閾值分布約束下進行BP神經網絡預測，輸出結果即為所求微震源點空間坐標。結合微震源反演模型，采用單隱層前饋網絡，三層拓撲結構分別為輸入層、隱含層和輸出層。輸入向量(到時差序列)個數n=20，輸出向量(微震源點坐標)個數m=3。隨機產生N組介于[-1，1]之間的權值和閾值分布。根據Kolmogorov定理，隱含層節點數理論上為2n+1個，即最大隱節點數Hmax=41，最小隱節點數Hmin=3，神經網絡結構為 20—41—3結構，共有20×41+41×3=943個權值，41+3=44個閾值。BP網絡預測結果即為所求微震源空間坐標，4種傳感器方案分別得出的反演定位結果與真實位置的標準差結果如表2所示。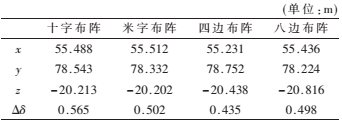

    通過表2可以看出PSO-BP混合反演算法在最優權值和閾值參數約束條件下的預測結果，即反演定位坐標(x，y，z)及定位誤差?駐?啄；由誤差值分布情況可以看出，網絡預測誤差取值分布在范圍0～0.6之間，符合微震源反演定位誤差要求，加入隨機擾動噪聲，反演預測結果可靠。
2.4 布陣方案仿真分析
    拾震器呈十字、米字、四邊形和八邊形布陣方案的震源定位誤差圖如圖3所示，圖中分別示出震源點在不同深度的定位誤差，深度按100 m步進。

圖3  震源定位誤差圖

    由圖3可以發現，十字布陣在0～400 m范圍內定位誤差小于1，米字布陣在0～700 m范圍內定位誤差小于1，在700～1 300 m范圍內米字布陣和四邊布陣定位誤差小于2，在1 300 m～1 800 m范圍內四邊布陣定位誤差小于1，在1 800 m～2 450 m范圍內八邊布陣定位誤差小于1。
2.5 拾震器數量與定位精度關系的仿真分析
    定位誤差隨拾震器數增加的變化曲線如圖4所示。圖4中隨拾震器個數的增加，定位誤差不斷減小，但當拾震器增加到一定數量時，定位誤差趨于平緩，反應了增加拾震器對定位誤差減小的效率問題。

圖4  定位誤差隨拾震器數增加的變化曲線

    仿真實驗中按4種布陣方式布陣，從5個拾震器逐個增加到90個，得出定位誤差隨拾震器數增加的變化曲線，縱坐標是E(i)誤差,橫坐標為拾震器個數。從實驗結果可以看出，當按十字方式布陣的拾震器數量從5增加到70個時，定位誤差成倍的減小，通過增加拾震器數量來提高定位精度的效果明顯；但是當數量達到70個之后趨于平緩，減少誤差的效率比較低，這時通過增加拾震器數量來提高精度的效果非常不明顯。出于成本考慮，拾震器數量采用50～70個的性價比較高。按米字方式布陣的拾震器數量增加到70個時，定位誤差趨于平緩；按四邊方式布陣的拾震器數量增加到66個時，定位誤差趨于平緩；按八邊方式布陣的拾震器數量增加到57個時，定位誤差趨于平緩。
3 結束語
    文中4種拾震器布陣方案的仿真比較結果和定位精度比較的仿真結果表明，利用微變網格射線追蹤法建立微震地質模型，對不同拾震器陣列方案的模型正演模擬研究得出的正演數據，在施加隨機擾動的情況下，利用PSO-BP算法反演推算震源位置，最后通過分析對比震源位置的誤差來證明各個布陣方案的特點，這可以十分有效地解決微震監測系統中拾震器如何布陣的問題。同時，根據得到的震源定位誤差圖分析，可以在拾震器利用率最高的情況下，選出準確、合理、有效的拾震器布陣方案。本研究對礦區微震定位監測系統中的拾震器布陣具有指導意義。
參考文獻
[1] 萬聚金，陳仲東.淺析煤礦超層越界開采的預防與治理[J].國土資源導刊，2012(5)：41-42.
[2] 平健，李仕雄，陳虹，等.微震定位原理與實現[J].金屬礦山，2010(1)：1-2.
[3] MENDECKI A J.Seismic monitoring in mines[M].London：Chapman and Hall ss，2010：12-15.
[4] KIJKO A，SCIOCATTI M.Optimal spatial distribution of seismic stations in mines[J].Int J.Rock Mech.and Mining Sci.and Geomechanics Abstracts，2012，32(6)：607-615.
[5] 牟宗龍，竇林名，鞏思園，等.礦井SOS微震監測網絡優化設計及震源定位誤差數值分析[J].煤礦開采，2009，14(3)：2-4.
[6] 張釙，劉洪，李幼銘.射線追蹤方法的發展現狀[J].地球物理學進展，2010，15(1)：36-45.
[7] Song Fuxian，TOKS?魻Z M N.Full-waveform based complete moment tensorInversion and source parameter estimation from downhole microseismic data for hydrofracture monitoring[J].Geophysics，2011，40(4)：13-16.
[8] 楊曉東.基于射線理論二維正演模型的微地震震源反演[D].北京：中國石油大學，2013.