文獻標識碼： A
DOI：10.16157/j.issn.0258-7998.2016.08.015
中文引用格式： 劉穩健，蔡華杰，朱維杰. 基于參數識別的PMSM無位置傳感器矢量控制[J].電子技術應用，2016，42(8)：67-69，73.
英文引用格式： Liu Wenjian，Cai Huajie，Zhu Weijie. Sensorless vector control of PMSM based on parameter identification[J].Application of Electronic Technique，2016，42(8)：67-69，73.
0 引言
隨著永磁材料性能的不斷提升和電力電子等技術的日益成熟，永磁同步電機（PMSM）由于其自身具有高效率、高轉動慣量比、體積小等優勢，在相關領域的應用越來越廣泛[1]。
在PMSM矢量控制系統中，電機轉子位置的檢測是關鍵一環，只有精確獲知轉子的位置，整個系統才能平穩運行。現有的PMSM無位置傳感器轉子位置檢測方法主要有：開環算法、觀測器估計算法和高頻注入法[2]。其中，滑模觀測器因其具有性能優越、結構簡單、魯棒性好等優點，受到了相關領域的高度重視[5-8]。
本文設計了一種新型的位置估計算法，將滑模觀測器（SMO）和電機參數辨識結合起來，利用改進的遞推最小二乘法在線辨識電機參數，將辨識值反饋到SMO中，以達到提高轉子位置檢測精度的目的。
1 永磁同步電機數學模型
永磁同步電機是具有強耦合性的復雜模型，所以在研究中一般將其抽象為簡單的數學模型，在dq坐標系下對PMSM建立數學模型如下。
電壓方程：
磁鏈方程：
其中，ud、uq為d軸、q軸電壓分量，Rs為定子電阻值， id、 iq為 d軸、 q軸電流分量，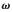
為轉子角速度，
為定子磁鏈d軸、q軸分量，Ld、Lq為d軸、q軸電感分量。
2 遺忘因子遞推最小二乘法在線辨識電機參數
最小二乘法是Karl Gauss于1795年提出的，他提出“未知量的最可能值是這樣一個數據，它使各次實際觀測值與計算值差的平方乘以度量其精度的數值以后所求得的和為最小”[9]。這一估計算法被廣泛用于系統辨識和參數估計。最小二乘法的最大缺陷是系統要處理大量數據，所以要完成對電機參數在線辨識的目的有很大困難。為了改進該方法，在此基礎上加入遞推的思想：
新估算值
舊估算值
修正項
依據此概念可得出遞推公式為：
上式中，
遞推思想在定常的參數識別中比較常用，但是在PMSM矢量控制系統中，電機參數（定子電阻值和電感值）不是固定不變的。所以如果采用遞推方法，由于數據不斷積累，就會造成“數據飽和”現象。為解決該問題，本文引入遺忘因子概念。
目標函數為：
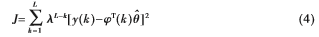
式中，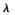
為遺忘因子，0<
<1。
由該目標函數可得出遺忘因子遞推最小二乘法參數估計公式推導結果：
式中遺忘因子一般選擇為：0.9<
<1。當
=1時，遺忘因子遞推最小二乘法變成遞推最小二乘法。
根據電機數學模型可得電機的狀態方程：
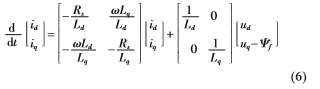
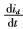離散化：
，T為辨識間隔時間，可得：
所以電機模型最小二乘法形式為：
由上式可知，電機參數定子電阻值Rs和電感值L均包含于等式右側矩陣，所以理論上可以利用遺忘因子最小二乘法進行辨識，唯一的未知量是永磁體磁鏈
觀察上式可知，永磁體磁鏈
只存在于iq中，在id中不存在。本文采用的是id=0的矢量控制策略，上式可以簡化為：
利用遺忘因子遞推最小二乘法對電機的兩個參數進行在線辨識，令
則：
式中，
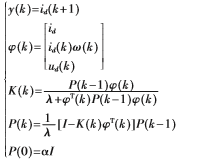
?琢取值范圍是104～1010。先利用上式得出a和b的數值，再利用a(k)和b(k)方程求解出Rs和L，從而辨識出電機參數。
3 滑模觀測器設計
滑模觀測器源于滑模變結構，即利用切換函數強迫狀態量沿滑模面運動，最終達到期望的狀態位置。已知電機反電動勢包含有轉子位置和轉速信息，根據電機數學模型構造如下滑模觀測器[10]方程：
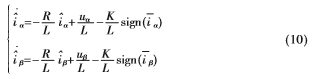
式中，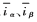
為
坐標系下的電流誤差；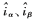
為電流觀測值；K為常量增益。sign(x)為符號函數：
電流誤差方程為：
利用Lyapunov穩定性準則函數保證滑模觀測器穩定性，構造Lyapunov函數：
對上式求導數，并代入誤差方程：
易知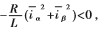
Lyapunov穩定性準則要求
，所以：
由此可得，欲使滑模觀測器穩定可靠，則：K>
構造滑模面為：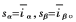
控制方法為函數切換控制：
u=ueq+Ksign(s(x))=e+Ksign(s(x))
系統進入滑動模態時，有：s(x)=0，
，經過有限時間間隔后
令電流估算方程中
得到
將在線辨識的定子電阻值和電感值反饋到滑模觀測器中，不影響其魯棒性，可改進SMO性能，減小電機參數變化帶來的不利影響，有效提高轉子位置估計精度，進而提高PMSM矢量控制系統整體性能。
4 仿真結果及其分析
仿真系統模型采用矢量控制，轉速設定1 500 r/min，采用速度環和電流環雙閉環控制。本文設計的控制系統電機參數為：額定功率550 W，額定電壓220 V，定子電感8.5 mH，定子初始電阻2.875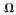 
，仿真時間設定為0.4 s。由于在實際工況中，電機定子電阻值和電感值基本不會在時間內有太大變化，所以不在同一次仿真中改變電機參數，通過與基于普通滑模觀測器矢量控制系統對比，直接仿真驗證電機參數變化后的系統性能。
4.1 基于普通滑模觀測器矢量控制系統仿真分析
從圖1可以看出，在電機定子電阻值達到3.25 
，而電感值減小到8 mH時，帶普通滑模觀測器的矢量控制系統電機實際轉速波動較大，同時趨于穩定的時間增加，在大約t=0.15 s時才逐漸穩定，說明該滑模觀測器的響應不夠迅速。同時，估計轉速對實際轉速的跟隨也不穩定。從圖2可看出電機轉子估計位置和實際位置有了較大誤差，主要是由于電機參數變化后，滑模觀測器參數沒有相應變化。誤差的累積嚴重時可導致系統崩潰，電機無法正常運行。說明在電機參數變化以后普通滑模觀測器的性能下降，不能準確估計電機轉子位置。本次仿真驗證了基于普通滑模觀測器的矢量控制系統在電機參數變化后系統整體性能下降明顯，不能滿足高精度控制要求。
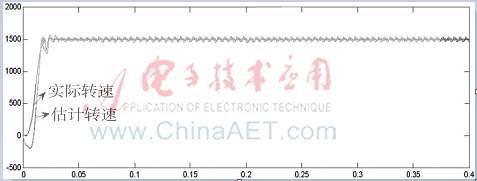
圖1 基于普通滑模觀測器矢量控制系統實際轉速和估計轉速對比
圖2 基于普通滑模觀測器矢量控制系統實際位置和估計位置對比
4.2 基于參數識別的PMSM矢量控制系統仿真分析
從圖3可以看出，轉速為1 500 r/min時，系統在0.08 s達到穩定狀態，證明本系統具有優越的快速響應。估計轉速在0.03 s以后實現對實際轉速的快速響應。但是在轉速較低時轉速明顯波動較大，這也是滑模觀測器存在的問題，即在電機低速時的性能并不理想，主要是由于反電動勢的值太小。由圖4可以看出，在大約t=0.07 s時，轉子估計位置與實際位置基本完全重合，主要是由于改進后的滑模觀測器參數能夠隨電機參數的變化而相應變化。說明了本系統位置估計的精確性很高，同時響應迅速。在t=0.07 s之前，轉速沒有達到1 500 r/min時，轉子位置估計誤差很大，這是滑模變結構自身抖振問題引起的誤差，但是在轉速穩定后估計誤差幾乎為0，間接說明滑模觀測器在高速時的優越性。本次仿真驗證了基于參數識別的PMSM矢量控制系統能夠很好地克服電機參數變化帶來的不良影響，整體性能表現優越。
圖3 基于參數識別的PMSM矢量控制系統實際轉速和估計轉速對比
圖4 基于參數識別的PMSM矢量控制系統轉子實際位置和估計位置對比
5 結論
本文創新性地將遺忘因子遞推最小二乘法在線辨識電機參數和滑模觀測器結合起來，很大程度上減小了在電機運行過程中參數變化對滑模觀測器性能的影響。本文設計的改進型滑模觀測器在估計轉子位置時具有良好的性能表現，同時在很大程度上提高了系統的整體性能。
參考文獻
[1] 王松.永磁同步電機的參數辨識與控制策略研究[D].北京：北京交通大學，2011.
[2] KANG J，HU B，LIU H，et al.Sensorless control of permanent magnet synchronous motor based on extended kalman filter[C].In：Preceeding of the International Conference on Services Science，Managent and Engineering，2009，567-570.
[3] WU G，XIAO X.Speed controller of servo system based on mras method[M].Gippsland，VIC.2009：1-5.
[4] YU C S，KAI S，HONG Y M.Permanet fiux identification of PMSM based on EKF with speed sensorless control[M].Glen dale，AZ.2010：2252-2257.
[5] ORLOWSKA K T，DYBKOWSKI M.Stator-current-based mras estimator for a wide range speed-sensorless induction-motor drive[J].Industrial Electronics，IEEE Trans.2010，57(4)：1296-1380.
[6] LIU S M，DING L J.Application of adaptive fuzzy sliding mode controller in pmsm servo system[C].In：Preceedings of the International Conference on Computing.Control and Industrial Engineering(CCIE)，2010，2：95-98.
[7] WANG Y H，ZHANG X Z，YUANG X F.Position-sensorless hybrid sliding-mode control of electric vehicles with brushless dc motor[J].IEEE Transactions on Vehicular Technology.2011，60(2)：421-432.
[8] FENG Y，ZHENG J，YU X H.Hybrid terminal sildingmode observer design method for a permanent-magnet synchronous motor control system[J].IEEE Transactions on Industrial Electronics.2009，56(9)：3424-3431.
[9] 龐中華，崔紅.系統辨識與自適應控制MATLAB仿真[M].北京：北京航空航天大學出版社，2009.
[10] Hongryel Kim，Jubum Son，Jangmyung Lee.A hign-speed sliding-mode observer for the sensorless speed control of a PMSM[J].IEEE Trans.on IE，2011，58(9)：4069-4077.