文獻標識碼： A
DOI：10.16157/j.issn.0258-7998.2016.09.020
中文引用格式： 曾憲陽，楊紅莉，郁漢琪，等. 基于單片機控制的旋轉倒立擺建模分析與系統設計[J].電子技術應用，2016，42(9)：76-79.
英文引用格式： Zeng Xianyang，Yang Hongli，Yu Hanqi，et al. The modeling analysis and system design of rotational inverted pendulum based on single chip microcomputer control[J].Application of Electronic Technique，2016，42(9)：76-79.
0 引言
倒立擺是一種研究控制理論的理想平臺，其結構簡單、成本低，是一個典型的多變量、快速、非線性和自然不穩定系統。旋轉倒立擺在外力的作用下，從一個穩定的平衡狀態自動轉移到另一個平衡狀態的過程中，既要求起擺迅速，又要求在到達新的平衡點時能快速進行穩擺控制[1-4]。
圖1為旋轉倒立擺結構圖。旋轉倒立擺的原理為：當電機帶動旋轉臂在水平平面內來回轉動時，擺桿由于慣性將會繞轉軸2在豎直平面內來回擺動，當能量達到一定數值時，擺動幅度將超過180°形成倒立狀態。通過單片機系統控制擺桿迅速倒立是本文研究的主要內容。首先建立數學模型，然后設計單片機軟、硬件系統，最后進行調試分析，形成旋轉倒立擺單片機控制系統。
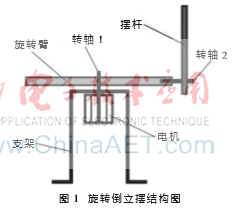
1 系統數學模型創建
建立數學模型前，設空氣阻力忽略不計。系統由電機和質量均勻的擺桿m組成，擺桿質心到轉軸2的距離為L，轉軸2軸心到轉軸1軸心距離為r，某時刻旋轉臂在水平面上轉動角度為?茲，擺桿在豎直平面內轉動角度為?琢，設擺桿和旋轉臂的角度以逆時針方向為正[5]。其受力分析如圖2所示。
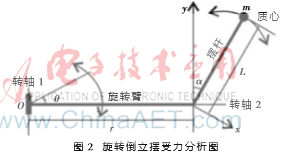
旋轉臂和擺桿一起動作，擺桿質心x、y方向的速度分量分別如下：
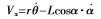
系統總動能T由4個部分組成：旋臂水平面內的轉動動能、擺桿豎直平面內的轉動動能、擺桿質心沿x軸方向和y軸方向的動能。由此可得到Lagrange函數：
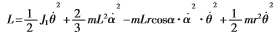
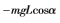
Lagrange方程：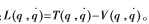
。其中，q是系統的廣義坐標，T為系統總動能，V為系統的勢能，L為拉格朗日算子。Lagrange方程表示為：
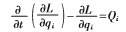
在倒立擺系統中i=1，2，q=(?茲，?琢)，?茲為旋臂角位移，?琢為擺桿角位移，Qi為系統沿該廣義坐標方向上的外力，得到以下方程組：
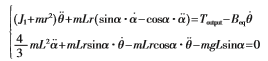
令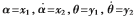
，得出系統線性化狀態方程：
根據表1相關參數，當旋轉倒立擺系統靠近平衡點時，得到如下線性化數學模型：
2 控制系統硬件電路設計
2.1 控制系統總體框圖
控制系統主要由單片機系統、驅動模塊、直流減速電機、角度傳感器、LCD液晶顯示模塊等組成。單片機通過實時采集角度傳感器數據，經分析得出擺桿當前狀態，通過計算得出相應控制量來控制電機轉動，從而改變擺桿狀態，使其達到預期控制的目的。系統總體框圖如圖3所示。
2.2 控制系統電路原理圖
圖4為控制系統傳感器及驅動原理圖。為保證控制精度和速度，采用增強型51單片機STC12C5A60S2[6]作為控制核心；電機驅動模塊采用L298N大電流電機驅動芯片，由單片機P2口部分口線控制；角度傳感器采用MPU6050 六軸運動處理組件，能檢測擺桿在垂直方向上的角度值，由P1口部分口線控制，中斷引腳接至單片機外部中斷0引腳。此外電路還包括LCD12864顯示電路及按鍵電路，用來實現人機交互及當前狀態顯示。
3 控制系統軟件設計
3.1 資源分配及程序流程
系統主要控制任務包括：角度數據采集與處理、電機驅動控制、按鍵輸入讀取、數據顯示等。其中數據顯示任務為非緊急事件，由主程序循環調用即可完成；角度數據采集與處理、電機驅動控制任務具有連貫性及較高的實時性，屬于周期性的緊急事件，應由定時器T0中斷服務子程序一并完成；按鍵輸入讀取任務屬于隨機性的緊急事件，應由外部中斷0子程序來完成。
定時器T0中斷服務子程序流程圖如圖5所示，主要執行讀取傳感器數據、卡爾曼濾波、PID調節任務，為避免中斷程序溢出，此三項任務的執行時間應小于5 ms，因此單片機外部晶振頻率選為24 MHz方能滿足速度需要。
3.2 控制調節算法
PID調節是按偏差的比例、積分、微分進行控制的一種閉環調節控制，原理框圖如圖6所示，其中r(t)為系統給定值，c(t)為實際輸出，u(t)為輸出控制量。引入PID調節算法可保證系統處于閉環控制狀態，并且能讓系統快速準確達到設置的平衡狀態[7-11]。
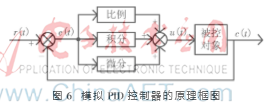
系統采用計算量較小的增量式PID算法，由模擬PID離散化得到在k-1時刻的輸出：
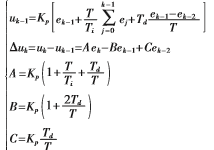
其中，T為采樣時間。單片機控制系統將采用恒定的采樣周期T，一旦確定A、B、C，只要使用前后3次測量的偏差值，就可以求出控制量。
3.3 系統抗干擾設計
由于角度傳感器采集到的數據含有噪聲信號，主要來自外界電磁干擾及角度傳感器本身的噪聲。在軟件系統中采用卡爾曼濾波算法[12-15]將噪聲濾去。設采樣率為200 Hz，對擺桿擺起發整個過程進行角度數據采集，經卡爾曼濾波前后圖像對比如圖7所示,其展示了擺桿從自然下垂狀態開始實現倒立的整過過程。擺桿靜止時刻自然下垂為平衡狀態Ⅰ，與垂直方向夾角為0°(圖7(b)中2段所示)。擺桿在電機帶動下獲取一定能量來回振蕩(圖7(b)中3所示），能量達到一定程度擺桿越過180°實現倒立，經過短時間幾次小的振蕩后(圖7(b)中4所示)，到達新的平衡狀態Ⅱ(圖7(b)中5所示)，實現了擺桿倒立。停止電機控制，擺桿將回到原平衡狀態Ⅰ，并在0°附近自由振蕩幾次后達到靜止(圖7(b)中6所示)。由于卡爾曼濾波在初始時刻濾波誤差較大，屬于盲區(圖7(b)中1所示)，軟件編程時應延時幾秒以避開盲區。
3.4 主要程序源碼
定時器T0中斷子程序代碼如下所示[16]：
void Timer0 interrupt 1 using 1
{
TH0=(65536-2500)/256;
TL0=(65536-2500)%256;//重裝初值
ReadMpu6050();//讀傳感器數據
KalmanFilter();//卡爾曼濾波
if(DelayCounter==2000) //計數判斷
{Motor0=PIDControl();//PID調節控制
DispBuffUpdata();} //更新顯示緩沖區
else DelayCounter++;
}
4 測試結果與結論
表2為擺起模式運行結果測量表。通過按鍵設置擺起模式，分別選擇擺起角度為45°～180°之間的數據，擺桿會在電機帶動下做往復擺動，擺角很快達到超過-60°～+60°。當擺桿角度接近180°時，通過PID調節，迅速使擺桿保持穩定倒立狀態，時間維持5 s以上。通過一系列實驗驗證，該旋轉倒立擺系統能完成任意角度的擺起，并能實現快速倒立，系統能很好地滿足設計要求。
參考文獻
[1] 王家軍，劉棟良，王寶軍.X-Z倒立擺的一種飽和非線性穩定控制方法的研究[J].自動化學報，2013，39(1)：92-96.
[2] 趙建軍，魏毅，夏時洪，等.基于二階倒立擺的人體運動合成[J].計算機學報，2014，37(10)：2188-2195.
[3] 周昆，孫明瑋，陳增強.快速顯式預測控制在倒立擺系統中的應用[J].儀器儀表學報，2014，35(9)：2037-2044.
[4] 李雪冰，馬莉，丁世宏.一類新的二階滑模控制方法及其在倒立擺控制中的應用[J].自動化學報，2015，41(1)：194-202.
[5] 吳愛國，張小明，張釗.基于Lagrange方程建模的單級旋轉倒立擺控制[J].中國工程科學，2005，7(10)：11-15.
[6] 南通國芯.STC12C5A60S2+系列單片機手冊[DB/OL].http：//www.stcmcu.com.
[7] 曹敏，徐凌樺.單神經元PID算法在倒立擺控制系統中的應用[J].微計算機信息，2009，25(1-1)：70-71.
[8] 楊智，朱海鋒，黃以華.PID控制器設計與參數整定方法綜述[J].化工自動化及儀表，2005，32(5)：1-7.
[9] 王述彥，師宇，馮忠緒.基于模糊PID控制器的控制方法研究[J].機械科學與技術，2011，30(1)：166-172.
[10] 陳新海，李言俊.自適應控制及應用[M].西安：西北工業大學出版社，1998.
[11] 王立新.模糊系統與模糊控制教程[M].北京：清華大學出版社，2003.
[12] 付夢印，鄧志紅，閆莉萍.Kalman濾波理論及其在導航系統中的應用(第二版)[M].北京：科學出版社，2010.
[13] DAUM F.Nonlinear filters beyond the Kalman filter[J].IEEE A&E Systems Magazine，2005，20(8)：57-69.
[14] KIM J，VADDI S S，MENON P K，et al.Comparison between nonlinear filtering techniques forspiraling ballistic missile state estimation[J].IEEE Transactions on Aerospace and Elec-tronic Systems，2012，48(1)：313-328.
[15] KALMAN R E.A new approach to linear filtering and prediction problems[J].Transactions of the AMSE Journal of Basic Engineering，1960，82：35-45.
[16] 譚浩強.C語言程序設計(第三版)[M].北京：清華大學出版社，2005.