陳偉利,陳國華
(湖南人文科技學院 數學與計量經濟系,湖南 婁底 417000)
摘要:針對基本蝙蝠算法存在的易陷入局部最優、后期收斂速度慢等問題,提出動態雙子群擬梯度蝙蝠算法。該算法利用蝙蝠脈沖發射頻率將蝙蝠種群動態地劃分為自由搜索種群和局部搜索種群兩個子群,在局部搜索子群中利用擬梯度方向指導蝙蝠搜索。為了驗證算法的有效性,通過對4個基準函數的實驗測試,實驗結果表明,該算法相對于基本蝙蝠算法具有較好的全局搜索能力和優化精度。
關鍵詞:蝙蝠算法;擬梯度;基準函數;最優值
0引言
蝙蝠算法(Bat Algorithm, BA)是一種新穎的群智能優化算法,是由劍橋大學學者 Yang Xinshe在2010年通過模擬蝙蝠的捕食行為而提出的一種優化算法[1]。該算法將優化問題的解看作是搜索空間中的微蝙蝠,搜索最優解的過程看成是微蝙蝠尋找食物的過程。在一定程度上粒子群優化(PSO)算法和和聲搜索(HS)算法是BA的一種特殊情況,而BA也被證明比粒子群優化算法和遺傳算法具有更高的搜索性能[2]。自蝙蝠算法提出以來,已成功地運用于多種優化問題的解決,如多目標優化[3]、工程優化[4]、聚類方法[5]、調度問題[6]、經濟負荷分配問題[7]等。參考文獻[8]總結了蝙蝠算法取得的進展,并提出了蝙蝠算法進一步研究的主要方向。雖然蝙蝠算法在許多優化問題中取得了很好的效果,但其本身也存在后期收斂速度不快和易陷入局部最優等缺點。針對蝙蝠算法的這些缺陷,許多學者提出了各自的改進方法,如模糊蝙蝠算法[9]、混沌蝙蝠算法[10-11]、Lévy飛行蝙蝠算法[12-13]。在對蝙蝠算法的改進中,多數學者集中在蝙蝠初始化和飛行方式的改進上[10-15],而對于改進蝙蝠的局部搜索策略的算法相對較少,基于此,本文提出動態雙子群擬梯度蝙蝠算法(PGBA)。通過仿真實驗表明,與基本的BA相比,PGBA具有更好的尋優能力和搜索精度。
1動態雙子群擬梯度蝙蝠算法
1.1設計思想
蝙蝠算法能夠成功地解決很多問題,但基本蝙蝠算法存在求解精度不高和收斂速度過慢的問題。筆者通過記錄蝙蝠群體在飛行時的各種參數,并對參數進行了簡單統計分析發現,控制蝙蝠群體自由飛行和局部搜索分配的脈沖發射頻率更新速度較快,而響度的變化卻并不大,這直接導致蝙蝠在局部尋優過程中由于飛行速度過快而不能很好地發現更優解。因此,為了提高蝙蝠的局部搜索能力,必須改變蝙蝠的響度更新方式。此外蝙蝠在局部搜索時是在最優解附近隨機生成一個解,既然局部搜索的目的是發現更好的解,那為什么不朝著最有利的方向搜索?受梯度在傳統算法中的高效性的啟發,本文引入擬梯度定義,用于指示函數的大致上升或下降的方向,指導蝙蝠的局部搜索。
定義給定某常數h,p維函數f(X)在點(x1,x2,…,xp)的相對于h的擬梯度向量定義為:
V=(v1,…,vp)
其中,vi=f(x1,x2,…,xi+h,…,xp)-f(x1,x2,…,xi,…,xp)。
1.2動態雙子群擬梯度蝙蝠算法步驟
綜上所述,本文提出擬梯度蝙蝠算法的步驟如下:
(1)初始化蝙蝠種群參數(蝙蝠的位置、飛行頻率、飛行速度、脈沖發射頻率、響度)。
(2)計算每只蝙蝠的適應度值,并得到最優適應度對應的蝙蝠位置(bestx),記錄最優適應度值。
(3)生成隨機數,將蝙蝠種群分為脈沖發射頻率小于隨機數(記為第一類)和大于隨機數(記為第二類)兩類。
(4)自由飛行。對步驟(3)分出的第一類,按照基本蝙蝠算法進行自由飛行。
(5)擬梯度局部搜索。對步驟(3)分出的第二類,首先令h=loudness,計算其擬梯度v,在最優位置附近按擬梯度方向生成一個局部解,xnew=xbest-v 。
(6)如果局部搜索不能找到更優解,視為響度太大搜索失敗,將該蝙蝠的響度更新為原先的α倍,即Anew=α×Aold。如果找到更優解,則更新蝙蝠位置,保持響度不變。
(7)對自由飛行和局部搜索之后的蝙蝠種群,如果找到更優解,則更新其脈沖發射頻率。更新方法為:rt+1i=r0i(1+e-γ×t)。
(8)對當前蝙蝠重新排序,找到最優蝙蝠所在位置,記錄最優值。
(9)滿足結束條件(達到精度或最大迭代次數),轉至步驟(10),否則轉至步驟(3),進行下一輪迭代。
(10)輸出相關結果。
2仿真實驗
為了驗證本文提出的算法的有效性,本文從相關文獻中選取4個標準測試函數(包括單峰和多峰函數)進行仿真實驗。

這是一個多峰函數,在x*=(0,0,…,0)取得理論最小值0。
利用擬梯度蝙蝠算法對4個標準的測試函數進行求解,并與基本的蝙蝠算法進行比較。算法的參數設置如下:在標準蝙蝠算法中,頻率范圍為[0,1],α=γ=0.9,蝙蝠數量為40,r0=0.1,響度初始化為隨機數,迭代次數為200次。擬梯度蝙蝠算法的參數設置與標準算法類似,僅改變脈沖發射頻率和響度調整幅度,即rate0=0.5,α=0.5。在上述參數設置下,每種算法運行30次,將兩種算法的最優結果、最差結果、平均結果和標準差統計如表1所示。

從表1可以看出,與基本蝙蝠算法(BA)相比,擬梯度蝙蝠算法(PGBA)明顯取得更好的尋優結果。從最優結果的角度看,BA在f1、f2、f4上都是成功的,但在f3上失敗。與參考文獻[15]中結果有差異,這里主要的原因在于種群的數量和迭代的次數設置不同; PGBA在4個函數上都取得成功,且其精度遠遠高于BA,尤其在函數f4上,其精度達到了10-16 。從平均結果看,PGBA在f3上表現欠佳,但仍遠好于BA,而在其他函數上則取得了非常理想的結果。為了更清晰地對比BA和PGBA,圖1~圖4給出了兩種算法在4個函數上的收斂曲線對比圖。
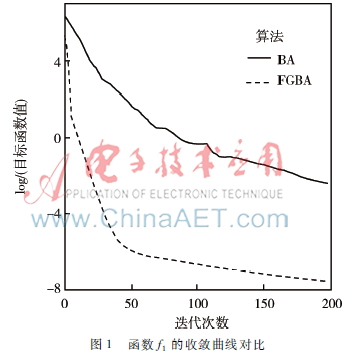



通過兩種算法的收斂曲線對比圖,可以發現PGBA相對BA具有更好的尋優能力,在函數f1和f2上,PGBA相對于BA不僅達到了更高的精度,而且在收斂速度上明顯要更快。而在f3和f4上,PGBA在開始迭代時其收斂速度并沒有優勢,但隨著迭代次數的增加,PGBA表現出了較強的局部挖掘能力。
3結論
針對基本蝙蝠算法收斂速度較慢和易陷入局部最優的問題提出了動態雙子群擬梯度蝙蝠算法。該算法動態地將基本蝙蝠種群劃分為自由搜索和局部搜索兩個不同的種群,在局部搜索種群中利用擬梯度方向指導蝙蝠的搜索。這一劃分既保證了算法的全局搜索能力,又提高了算法的局部搜索能力。實驗表明,該算法具有較好的全局搜索能力和較高的搜索精度。
參考文獻
[1] Yang Xinshe. A new metaheuristic batinspired algorithm[M].Nature inspired cooperative strategies for optimization (NICSO 2010). Springer Berlin Heidelberg, 2010: 6574.
[2] Yang Xinshe. Nature Inspired Metaheuristic Algorithms (2nd Edition)[M]. Frome, UK: Luniver Press, 2010: 97104.
[3] Yang Xinshe. Bat algorithm for multiobjective optimization[J].International Journal of BioInspired Computation, 2011, 3(5):267274.
[4] Yang Xinshe, GANDOMI A H. Bat algorithm: a novel approach for global engineering optimization[J]. Engineering Computation, 2012, 29(5):267289.
[5] KOMARASAMY G, WAHI A. An optimized kmeans clustering technique using bat algorithm[J]. European Journal of Scientific Research, 2012, 84(2):263273.
[6] 盛曉華,葉春明. 蝙蝠算法在PFSP調度問題中的應用研究[J]. 工業工程,2013,16(1):119124.
[7] GHERBI Y A, BOUZEBOUDJA H, LAKDJA F. Economic dispatch problem using bat algorithm[J]. Leonardo Journal of Sciences, 2014, 13(24): 7584.
[8] Yang Xinshe, He Xingshi. Bat algorithm: literature review and applications[J]. International Journal of BioInspired Computation, 2013, 5(3): 141149.
[9] KHAN K, NIKOV A, SAHAI A. A fuzzy bat clustering method for ergonomic screening of office workplaces[M]. Third International Conference on Software, Seruices and Semantic Techdogies S3T 2011. Springer Berlin Heidelberg, 2011,101:5966.
[10] LIN J H, CHOU C W, YANG C H, et al. A chaotic Levy flight bat algorithm for parameter estimation in nonlinear dynamic biological systems[J]. Computer and Information Technology, 2012, 2(2): 5663.
[11] 劉長平, 葉春明. 具有混沌搜索策略的蝙蝠優化算法及性能仿真[J]. 系統仿真學報, 2013, 25(6):11831188.
[12] 劉長平,葉春明. 具有Lévy飛行特征的蝙蝠算法[J]. 智能系統學報,2013,8(3):240246.

