張彥清， 劉大銘， 白冰， 李春樹

　　（寧夏大學 物理電氣信息學院，寧夏 銀川 750021）

     摘要：目前離心式壓縮機透平轉速預測難以實現，雖然引入了基于Elman神經網絡的離心式壓縮機透平轉速預測方法，但當離心式壓縮機轉速變化比較大時，該預測方法的預測精度就明顯下降。針對這一現象，提出了一種基于外反饋Elman的離心式壓縮機透平轉速預測方法。在標準Elman神經網絡的基礎上加一個由輸出到輸入的外反饋，通過帶外反饋的Elman神經網絡實現對離心式壓縮機透平轉預測。仿真實驗結果表明，所提出的帶外反饋的Elman神經網絡預測方法預測精度較高，特別在轉速變化較大時，收斂速度快，穩定性高。

　　關鍵詞：離心式壓縮機；轉速預測；外反饋；神經網絡

0引言

　　離心式壓縮機是一種葉片式旋轉機械，透平是帶動壓縮機轉動的關鍵部分，但喘振作為離心式壓縮機不穩定特性之一，這種現象的產生會影響到透平部分的運行，進而影響到壓縮機轉速。隨著對壓縮機研究的深入，不斷有新的系統辨識方法被應用到壓縮機的研究上。2000年，王麗春等人利用BP神經網絡對離心式壓縮機性能進行預測［1］，主要是針對壓縮機壓比進行預測，但預測結果只是具有良好的一致性；2008年，厲勇提出利用Elman神經網絡預測壓縮機性能的方法［2］，基本上能夠反映系統的運行狀況，但模型精度不高；2009年，王沛禹利用Elman神經網絡對離心壓縮機進行性能建模［3］，建立的網絡基本能夠反映壓縮機局部性能特點，這些都對以后基于Elman神經網絡的離心式壓縮機透平轉速預測具有很大指導意義。研究時發現，利用Elman神經網絡能夠透平轉速實現較高精度的預測，但是當轉速變化很大時預測精度就降低了。針對這一問題，本文提出在標準的Elman神經網絡基礎上加一個由輸出到輸入的外反饋，選定輸入量與輸出量來實現轉速的預測。結果表明，帶外反饋Elman神經網絡能夠實現高精度預測，特別是在轉速變化比較大時，帶外反饋的Elman神經網絡也能快速準確地實現對轉速的預測。

1帶外反饋的Elman神經網絡

　　Elman神經網絡除了輸入層、隱層、輸出層單元外，還有一個特殊的聯系單元。聯系單元用來記憶隱層單元以前時刻的輸出值，它使該網絡有動態記憶的功能。如圖1所示，神經網絡中有一個由A到B內反饋，此反饋連接使得網絡能夠用來檢測和生成時變模式。

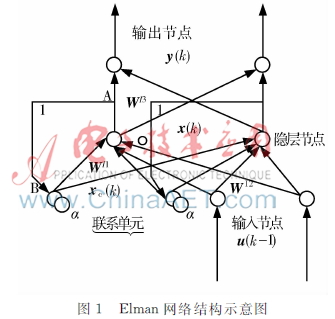
　　設網絡的輸入層有r個節點，隱層與聯系單元有n個節點，輸出層有m個節點，則網絡輸入u為r維向量，隱層輸出x及聯系單元輸出xc為n維向量，網絡輸出y為m維向量，連接權WI1為n×n維矩陣，WI2為n×q維矩陣，WI3為m×n維矩陣，α為自連接反饋增益因子。Elman神經網絡的數學模型：

　　x(k)=f(WI1xc(k)+WI2u(k－1))(1)

　　xc(k)=αxc(k－1)+x(k－1)(2)

　　y(k)=g(WI3x(k))(3)

　　設第k步時實際輸出為yd(k)，則網絡誤差函數為：

　　E(k)=12(yd(k)－y(k))T(yd(k)－y(k))(4)

　　根據梯度下降法分別計算E(k)對連接權偏導數并使其為0，得網絡的學習算法:

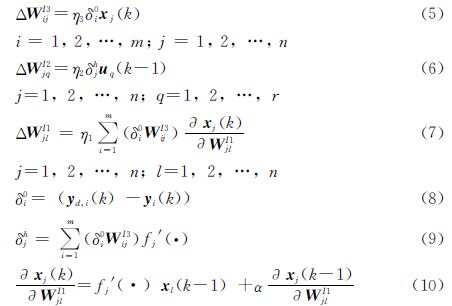
　　其中,η1、η2、η3分別是WI1、WI2、WI3的學習步長。

　　由于各層神經元的反饋信息都會影響到神經網絡的信號處理能力，為進一步提高Elman網絡性能,就要充分利用輸出層節點和承接層節點。因此基于上述理論對Elman神經網絡進行了修改，在輸出層和輸入層之間加一個反饋，如圖2所示。

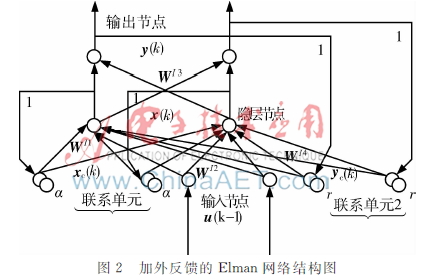
　　網絡增加的輸出節點反饋稱為聯系單元2，將它放在第1層， γ為反饋增益因子，權值為WI4。加入了外反饋Elman神經網絡的數學模型后要將式(1)改為：

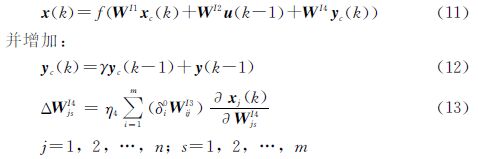
　　xj(k)WI4js=fj′(·)ys(k-1)+γxj(k-1)WI4js(14)

　　相對Elman網絡，加了外反饋的網絡動態性能得到增強，從而提高了網絡每次迭代的效率。

2離心式壓縮機參量選擇

　　2.1離心式壓縮機透平分析

　　針對現離心式壓縮機組的情況將其分兩部分：透平和壓縮機組。透平原理是將高溫、高壓氣體具有的熱能轉換為機械能以驅動壓縮機。蒸汽透平有3個控制閥門，分別為V1、V2與V3，各閥門控制情況如表1所示。通過表1，認為V1閥門是蒸汽透平的主要控制量，直接影響透平轉速的大小。

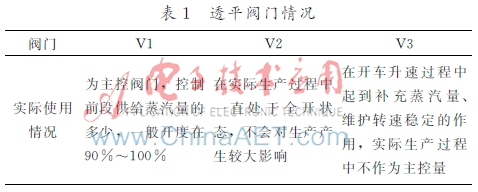
　　情況為主控閥門，控制前段供給蒸汽量的多少，一般開度在90%~100%在實際生產過程中一直處于全開狀態，不會對生產產生較大影響在開車升速過程中起到補充蒸汽量、維護轉速穩定的作用，實際生產過程中不作為主控量

　　確定V1閥門為主要控制量,減少了預測中的參量。當對壓縮機變量信息進行采集時，只調節V1閥門開度，利用組態軟件即可得到壓縮機狀態量的數據。

　　2.2壓縮機狀態量分析

　　離心式壓縮機的數據采集主要是給壓縮機施加階躍信號。流體在流動過程中不是一維而是三維的,即在采集的數據中存在噪聲，需要通過濾波來消除噪聲,同時利用MATLAB對數據進行平滑處理［4］。接著將上述數據導入到MATLAB軟件對應的程序中。其中，V1是V1閥門動作；Q蒸汽是蒸汽供給量；QCO2出是CO2出口流量；QCO2入是CO2入口流量；T1與P1分別是一段入口溫度與壓力；T8與P8分別是4段出口溫度與壓力。分析結果如圖3所示。

　　從圖3可以看出V1的變化直接影響n的變化，同時在n帶動下氣體壓力從P1上升到P8過程中,P1不斷被抽走，造成前段壓力降低，同時n會對P1產生影響，進而改變壓比使流量發生改變。

　　為更好分析各變量間相關性，把上述數據用SPSS210的Spearman法進行分析［5］。變量之間的相關性越強，相關系數越靠近于1或-1。分析結果如表2所示。

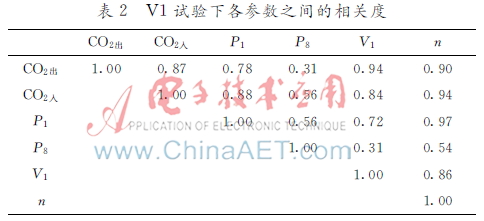
　　轉速和壓力的相關性最大是由于在分析試驗過程中兩者相關性最強烈，因此受到離心式壓縮機系統的時序影響，在時序相對較早的量往往被認為是主動量。通過分析，刪除相關度較少的因子，減少轉速預測時的輸入，降低仿真過程中的復雜度，最終確定實驗的輸入量和輸出量如表3所示。表3透平轉速預測的輸入量和輸出量控制量V1閥門輸入量CO2入、CO2出、V1、P1輸出量n

3仿真實驗

　　3.1轉速預測

　　V1閥門的改變會使其他狀態量也相應改變，從而會間接影響轉速的變化，以此對離心式壓縮機轉速進行預測。加載所要訓練的參數，利用MATLAB 導入神經網絡，給定系統初始和期望之后，系統根據期望得到參數取值和偏差從而確定神經網絡系統模型。然后選閥門打開過程中的另外27組數據對產生的神經網絡模型進行驗證，如圖4和圖5所示。

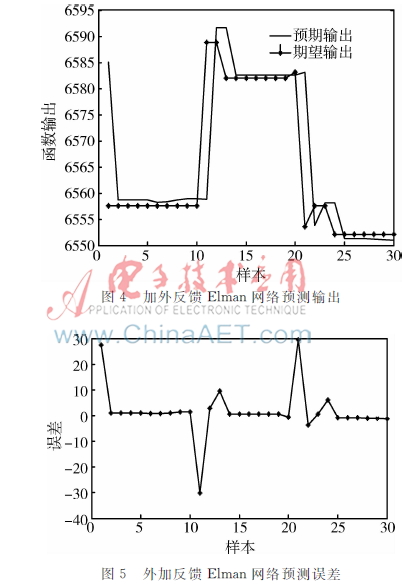
　　3.2與Elman神經網絡預測誤差的比較

　　相同情況下用Elman神經網絡預測壓縮機透平轉速，轉速預測誤差的仿真結果如圖6和表4所示。

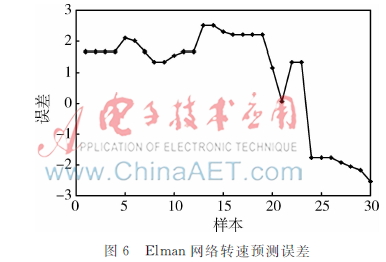
　　從表4可以看出：Elman神經網絡和帶外反饋Elman神經網絡在對轉速進行預測的收斂速度上都比較理想。在轉速變化相對穩定的情況下，Elman神經網絡和帶外反饋的Elman神經網絡都有較高的預測精度。但是，當轉速突然變化很大時，帶外反饋的Elman神經網絡能夠通過自身內、外反饋的調節快速、準確地調整到穩定狀態，并且預測誤差的能力與轉速變化之前相比基本上不變。這也說明了基于帶外反饋的Elman神經網對壓縮機透平轉速預測是可以被廣泛應用的。

4結論

　　離心式壓縮機系統是一個高復雜性、大延時系統，這樣高復雜的一個系統若使用傳統方法對其轉速進行預測，誤差較大。若使用BP神經網絡這樣一個多層前饋神經網絡［6］，又或者只含有一個內反饋Elman神經網絡，由于神經網絡包含的各層神經元的反饋信息都會影響到整個神經網絡的信號處理能力，因此為了充分發揮神經網絡的作用，要盡可能地把每層神經元的反饋信息充分利用起來。本文在Elman神經網絡的基礎上加一個外反饋，將輸出層的信息通過外反饋再反饋到輸入層，充分利用了輸出層的反饋信息。高精度的預測、預測收斂速度快以及預測誤差的趨于一致性都充分證明了對Elman神經網絡加外反饋的可行性。

參考文獻

　　［1］ 王麗春，樊會元. 離心式壓縮機性能預測的神經網絡方法［J］. 華東冶金學院學報, 2000,17(2):142145.

　　［2］ 厲勇. 基于模糊神經網絡的離心壓縮機的性能研究［D］.昆明：昆明理工大學,2009.

　　［3］ 王沛禹,厲勇.Elman神經網絡用于離心壓縮機的性能模型辨識［J］.硅谷,2009（14）:20.

　　［4］ 叢爽.面向MATLAB工具箱的神經網絡理論與應用［M］.合肥:中國科學技術大學出版社,1998.

　　［5］ 朱星宇,陳勇強.SPSS多元統計分析方法及應用［M］.北京:清華大學出版社,2011.

　　［6］ 蔣良孝,李超群.基于BP神經網絡的函數逼近方法及其MATLAB實現［J］.微型機與應用，2004，23(1):5253.