摘 要： 不同于一般社區劃分衡量標準——模塊度Q值，從社區結構本質出發，提出一種用關聯系數評判社區劃分好壞的方法，即求社區內部連接與外部連接的關聯系數。該方法不但能克服模塊度Q值只適用于無向無權網絡的缺陷，而且更符合社區結構的定義。
關鍵詞： 衡量標準；模塊度；關聯系數；社區結構
0 引言
物以類聚，人以群分。許多社會網絡隨著時間逐漸演變形成它們自身的社區。它們有一個共同特性——社區結構。整個網絡由若干社區構成，每個社區內部節點之間的連接相對緊密，而社區之間的節點連接相對稀疏[1]。
社區劃分的研究迄今已有很長歷史，學者們已研究出多種劃分算法，如GN分裂算法[2]，Newman快速算法[3]、基于Laplace矩陣的譜平分算法[4]、Kernighan-Lin算法[5]等。這些算法有一共性：用模塊度量Q[6]作為算法終止條件，同時也作為衡量社區劃分好壞的標準。
受Q值啟發，衡量標準也可從社區內部連接強度與社區之間連接強度的關聯系數出發，能直觀地符合社區結構定義[7]，兩者的關聯系數越小，同時內部連接值越大，之間連接值越小，則劃分結果越好。本文利用該思想首先闡述了在劃分算法中占重要位置的關聯系數，然后提出基于此的算法，最后將算法實驗于城市社區劃分應用場景，并將本文算法與基于Q值的社區劃分算法結果進行比較，結果表明本文提出的算法是切實可行且有效的。
1 社會網絡結構相關定義
1.1 社會網絡結構
定義 信息圖[8]：包含n個節點的圖G=（V，E，M），V是節點集合，節點vi有屬性集VA={va1，va2，…，vam}。E是邊集合，邊ei有屬性集EA={ea1，ea2，…，eal}。M為兩節點共享鄰居節點數的矩陣，簡稱共鄰矩陣，矩陣元素Mij=eikekj，其中eik、ekj分別表示vi和vk、vj和vk之間是否存在鏈接。
信息圖的連接強度矩陣元素Aij表示vi和vj的連接強度，它綜合了節點屬性、鏈接屬性和共鄰屬性。
1.2 關聯系數定義
設有曲線sin（t）和cos（t），取t=0，1，2，…，10時刻的正、余弦序列{sin（0），sin（1），…，sin（10）}，{cos（0），cos（1），…，cos（10）}，則兩曲線在各t時刻的關聯系數如下：
其中，（min）和（max）為兩曲線在同一時刻對應的最小差和最大差；（t）為兩曲線在t時刻的序列差；ρ為分辨系數，在0~1之間，通常取0.5。
（t）越小，即在t時刻兩曲線的關聯系數越小，兩者相關性越小。
2 基于關聯系數的社區劃分算法
2.1 算法定義
（1）節點屬性
vi和vj屬性集為VAi和VAj，構成帶夾角的空間向量，夾角越小表明兩節點屬性越相似。因此，用夾角余弦計算屬性相似度：
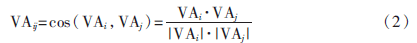
（2）鏈接屬性
為與實驗數據保持一致，這里用簡單的距離dij表示vi和vj的鏈接屬性，并用最大距離dmax將其歸一化：
（3）共鄰屬性
兩節點的共鄰數目越多，表明它們的間接聯系會越頻繁，則劃分至同一社區的概率會變大。因此共鄰屬性為：
（4）連接強度
節點之間連接強度綜合考慮三因素：
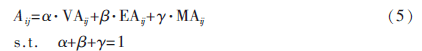
（5）互信息量NMI[9]
NMI是社區結構已知的算法評價標準，即算法發現社區結構與真實社區結構的一致性程度。若兩者完全一致，則NMI為1，通常NMI∈（0，1）。定義公式為：
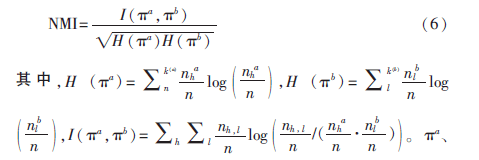πa、πb分別表示真實社區和算法發現的社區結構。k（a）表示社區結構πa中的社區數量，nha表示社區結構πa中第h個社區的節點數，nh，l表示同時在πa中的第h個社區，πb中的第l個社區的節點個數。
2.2 算法實現
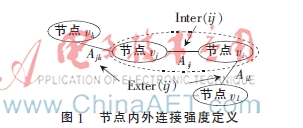
社會網絡中節點的連接強度如圖1所示，判斷兩節點能否凝聚至同一社區，需計算社區內部連接強度Inter（ij）和外部連接強度Exter（ij）之間的關聯系數。
兩者的計算公式分別如下：
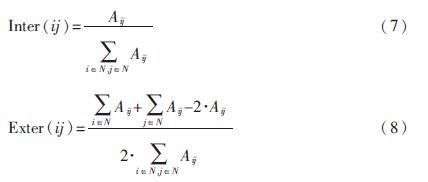
Inter（ij）表示社區內部連接強度占所有連接強度之比，Exter（ij）表示與社區內部相連的外部連接強度占所有連接強度之比。當Inter（ij）和Exter（ij）關聯系數越小，同時Inter（ij）越大、Exter（ij）越小時，表明社區內部的連接強度越大于外部，將該節點對凝聚至同一社區，會使得社區結構越穩定。
Inter（ij）和Exter（ij）關聯系數計算公式如下：
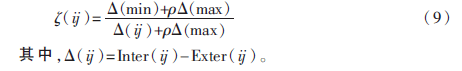
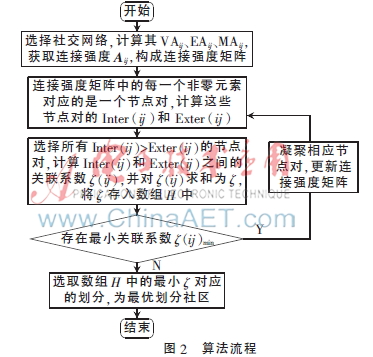
基于關聯系數的社區劃分算法（Community Detection Algorithm Based OnCorrelation Coefficients，CDACC））采用凝聚思想，逐步將社區節點對進行凝聚，具體的處理流程如圖2所示。
3 實驗及分析
（1）數據預處理
獲取南京市主城區數據，視各區內的社區為節點，抓取節點屬性{人口、年齡、人均占地面積}和節點之間距離。
約束條件：以vi為中心，長度D為直徑作圓，則在圓形區域內的節點記為vi的鄰居節點。
（2）參數選擇
式（5）中的參數用單一屬性方法獲取，即假設認為只有節點屬性對社區劃分有影響，計算得最優關聯系數和?灼1；同理得鏈接屬性和共鄰屬性的最優關聯系數越小，表明該屬性對社區劃分的影響力越大。因此，參數?琢、?茁、?酌的權重分配為：
由于本文算法是受基于Q的凝聚算法啟發，故將本文算法與經典凝聚算法——CNM[10]、凝聚算法的改進CDASW[11]進行比較，并利用互信息量衡量劃分結果。
（3）實驗分析
首先，用單一屬性法得由此看出：在城市社區中，鏈接屬性、節點屬性、共鄰屬性對劃分結果影響力依次減小。
利用式（10）將該權重分配與其余4組隨機數比較，得到結果如表1所示。
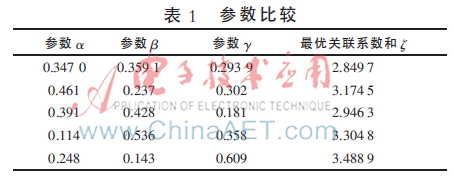
因此，在最優參數條件下，將本文算法CDACC、CNM、CDASW劃分結果與真實城市社區結構進行比較，結果如圖3所示。
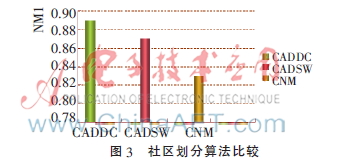
由圖3可知，在城市社區中，CDACC、CDASW、CNM算法的劃分準確率依次降低，這不僅驗證了城市社區的劃分需要綜合考慮節點屬性、鏈接屬性和共鄰屬性，還證明了CDACC算法的切實可行性。
4 結論
本文針對社區結構發現問題，提出了基于關聯系數的社區劃分算法。該算法在綜合考慮節點屬性、鏈接屬性和共鄰屬性的基礎上，計算社區內部和之間的連接強度，并計算兩者的關聯系數，依次選擇關聯系數最小的節點對進行凝聚。此外，將該算法實驗于城市社區，劃分出的社區結構與真實結構相比具有較高的準確性。但是，本文算法復雜度較高，適用于中小型網絡。因此，需要進一步探討算法，減少其復雜度，以便能夠適用于各種大型的復雜網絡。
參考文獻
[1] 鄭浩原，黃戰.復雜網絡社區挖掘——改進的層次聚類算法[J].微型機與應用，2011，30（16）：85-88.
[2] NEWMAN M E J， GIRVAN M. Finding and evaluating community structure in networks[J]. Physical Revew E， 2004， 69（2）：26113.
[3] NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Physical Review E， 2004，69：06613.
[4] Ruan Jianhua， Zhang Weixiong. An efficient spectral algorithm for network community discovery and its applications to biological and social networks[C]. Seventh IEEE International Conference on Data Mining， ICDM 2007， 2007：643-648.
[5] KERNIGHAN B W， LIN S. An efficient heuristic procedure for partitioning graphs[J]. Bell System Technical Journal，1970，49（2）：291-307.
[6] NEWMAN M E J. Modularity and community structure in networks[J]. Proc Natl Acad Sci USA， 48109-1040， 2006，103（23）：8577-8582.
[7] NEWMAN M E J. Detecting community structure in networks[J]. The European Physical Journal B， 2004，38：321-330.
[8] Tang Jin， Jiang Bo， Chang Chinchen， et al. Graph structure analysis based on complex network[J]. Digital Signal Processing， 2012， 22（5）：713-725.
[9] ALCOSER， JEFFREY J. Behind our sociality（or social capital）： evolution， the rule of 150， and reading others[J]. Behind our sociality， 2014， 8（5）：18-25.
[10] CLAUSET A， NEWMAN J， MOORE C. Finding community structure in very large networks[J]. Physical Review， 2004，70（6）：66-111.
[11] 李孝偉，陳福才，劉力雄.一種融合節點與鏈接屬性的社交網絡社區劃分算法[J].計算機應用研究，2013，30（5）：1477-1480.