摘  要： 針對現有目標拆卸序列求解方法在拆卸并行性規劃和計算效率上存在不足的情況，提出了一種目標拆卸序列優化算法。基于球面映射、非正交干涉矩陣以及復合拆卸路徑判別等方法的運用與改進，研究了零部件可拆卸性分析方法；應用分層圖方法，對目標零件進行定位，結合子裝配體識別法，去除冗余拆卸步驟，并提高拆卸過程的并行性。通過實例對該方法的有效性進行了驗證。

　　關鍵詞： 目標拆卸；可拆卸性分析；子裝配體識別

0 引言

　　研究裝配體在虛擬環境中的拆卸順序與路徑，對于簡化產品結構、減少制造成本、提高可維修性具有重要價值。而實際維修過程中針對特定故障零件的拆卸十分常見，因此研究目標拆卸序列規劃（Selective Disassembly Sequence Planning，SDSP）對于增強維修人員維修技能、提高維修效率具有重要意義。

　　近20年間，學者提出各種拆裝序列規劃算法。智能啟發式算法在求最優解方面具有高效性，被廣泛用于解決序列規劃問題，常見的有遺傳算法[1]、蟻群算法[2]、模擬退火法等，但此類方法難以對目標拆卸序列進行優化。關系矩陣[3]可從幾何角度生成可行拆卸序列，但只能處理零件沿正交坐標軸拆卸的情況。于嘉鵬[4]等提出擴展干涉矩陣較好地解決了非正交方向可拆卸性分析的問題，但零件初始拆卸方向的判定較為繁瑣，且生成序列對于目標拆卸存在冗余拆卸步驟。

　　本文針對目標零件拆卸方法，在分析零件可拆卸性的基礎上，通過基于零件分層圖的子裝配體識別，定位拆卸目標，去除冗余拆卸步驟，并提高拆卸并行化程度，生成最終目標拆卸序列。通過Delphi對三維CAD軟件SolidWorks的二次開發相關技術構建了目標拆卸序列智能規劃系統，進行相關理論驗證。

1 可拆卸性判別

　　1.1 初始拆卸方向與初始可拆卸性

　　利用可見圖（Visibility Maps）球面映射Vmap投影[5]，將零件接觸面fi的可見方向投影到單位球上，記為Vmap（fi）。所有接觸面可分為平面接觸面與圓柱接觸面兩種類型（在本文中將螺紋連接簡化為圓柱接觸面）。平面接觸面的Vmap為以S為極軸的單位半球（如圖1（a）所示）。柱面接觸面的Vmap為單位球中與S同向的極軸（如圖1（b）所示）。

　　設裝配體零件數為N，A為與零件ri接觸的所有零件，零件ri與A的所有接觸面為fi，其中1≤i≤N。對ri中與A的所有接觸面的Vmap進行求交運算，可得ri相對于A的可拆卸方向VA（ri），VA（ri）=Vmap（fi）。圖2所示為零件ri可沿區域S內的方向拆卸。

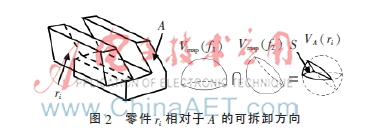
　　根據Vmap投影求解初始拆卸方向，本文提出零件初始可拆卸性定義如下：

　　定義1.初始可拆卸性。零件ri與其所有接觸面經Vmap求交運算所得的可拆卸方向不為空，并且不考慮零件沿此拆卸方向前進的過程中與其他零件所產生的干涉，則認為此零件具有初始可拆卸性。

　　1.2 非正交干涉矩陣

　　針對非正交方向，除了基礎件的絕對坐標外，還應將各個零件建模時與其幾何特征相關的相對坐標（Dix，y，z）定位于裝配空間之中。

　　若在絕對坐標系中，零件r1沿+X方向與零件r2無干涉，則零件r2沿-X方向與零件r1無干涉，即干涉矩陣的列包含列所屬零件沿該軸負方向移動時的干涉情況。因此可將方向集簡化為S={+X，+Y，+Z，±Dix，±Diy，±Diz}。

　　稱A=[aijs]9×N×N為非正交干涉矩陣（Non-Orthogonal Interference Matrix，NOIM）。NOIM可通過基于軸向包圍盒及CAD干涉分析內核的兩級干涉檢測獲取[6]。

　　1.3 復合拆卸路徑

　　對于具有初始可拆卸性且拆卸路徑有轉折的零件，稱其具有復合拆卸路徑。

　　設零件r1具有初始拆卸方向S，r1的初始接觸面為A，當ri沿S方向以一定的步長f位移至P0位置時，ri與A不再接觸，稱P0為零件ri的節點。若零件具有初始拆卸方向，但位移至節點P0之前與其余零件發生干涉，則此零件不可拆。對于這種情況現有方法[6]無法解決。對此本文提出一種零件復合拆卸路徑的判別方法。

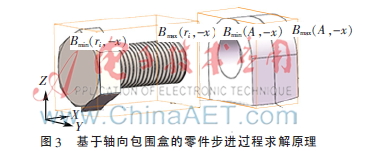
　　確定零件ri從初始位置至節點P0的距離L以及位移步長f。如圖3所示，利用基于軸向包圍盒（AABB包圍盒）求出ri與A在初始拆卸方向-X上的包圍盒極值點：Bmin（ri，-x）、Bmax（ri，-x）、Bmin（A，-x）、Bmax（A，-x）。

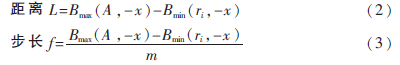
　　式中m為移動過程的步進次數。零件ri向節點P0步進移動時，若步長f太大，有可能會遺漏移動過程中的干涉情況；若步長f太小，則會增加運算量，增加干涉檢測時間。步進次數m一般取8~10，使步長f相對于零部件幾何尺寸比較合適。

　　ri每前進一個步長對其進行干涉檢測，若出現干涉則判定零件不可拆；若無干涉現象，則在節點P0處沿  +X，+Y，+Z三個方向進行干涉檢測，如存在某一方向無干涉，則判定零件可拆卸，存在復合拆卸路徑，系統記錄其路徑并對NOIM的對應項進行修正，否則判定不可拆卸。若初始拆卸方向為正交軸方向，在節點P0只進行兩個方向的干涉檢測即可。

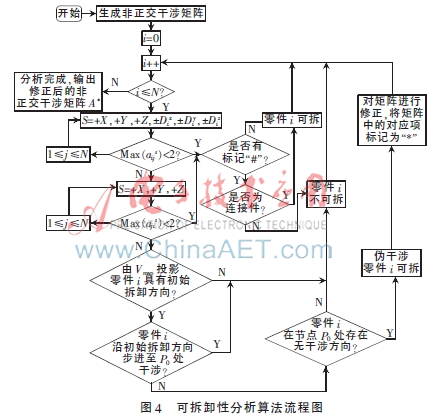
　　1.4 可拆卸性分析算法流程

　　本文提出零件的可拆卸性分析算法流程如下：

　　（1）對所有零件進行掃描，生成初始非正交干涉矩陣A=[aijs]9×N×N，其中S={+X，+Y，+Z，±Dix，±Diy，±Diz}。默認aiis=0。本文將螺紋連接默認為圓柱面接觸，故若aijs=0且i為螺紋連接件固定于零件j上，則將aijs標記為“#”（表示雖存在無干涉方向，但連接方式為螺紋連接，被連接件不可拆卸）。

　　（2）對零件判斷其NOIM所對應行向量除“#”外所有元素是否為0。若不是，則零件沿該方向與其他零件有干涉，進入下一步；若是，則判斷是否存在“#”，不存在則零件可拆，存在則判斷其是否為連接件，是則零件可拆，不是則零件不可拆。

　　（3）對零件i判斷其標準正交軸方向S={±X，±Y，±Z}的NOIM所對應列向量除標記“#”外的所有元素是否為0（即標準正交軸負向）。若不是，則零件沿該方向與其他零件有干涉，進入下一步；若是，則判斷是否存在“#”，不存在則零件可拆，存在則判斷其是否為連接件，是則零件可拆，否則零件不可拆。

　　（4）根據Vmap投影判斷其初始拆卸可行性。若無初始拆卸方向則該零件不可拆，若有初始拆卸方向則進入下一步。

　　（5）零件i以一定步長f沿初始拆卸方向移動至節點P0處，零件每移動一個步長，對其進行干涉檢測。若存在干涉現象則零件不可拆卸，若無，進入下一步。

　　（6）判斷零件i在節點P0處是否具有可拆卸方向。若是，則零件可拆，記錄其復合拆卸路徑，對NOIM進行修正，將對應項的值“1”標記為“*”，表示零件i沿此方向與j雖有干涉，但零件i仍可拆卸，系統返回并掃描下一零件；若不是，則判定零件不可拆，系統返回并掃描下一零件。

　　當i>N時，算法結束，輸出修正后的NOIM—A*。算法流程圖如圖4所示。

2 目標拆卸序列規劃

　　在機械產品的維修過程當中，通常只需對特定的故障零件進行維修或更換，而不必進行完全拆卸，這種拆卸指向性、目的性較強，稱之為目標拆卸（Selective Disassembly）。

　　2.1 基于圖方法的目標零件定位

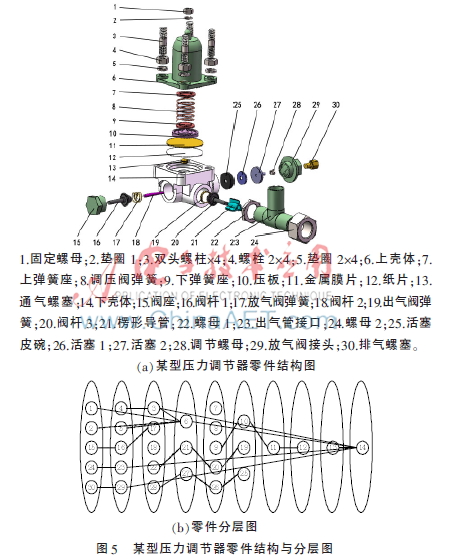
　　對于得到的NOIM，參考文獻[7]采用基于同步約束解除的方法構建零件分層圖。以圖5（a）所示壓力調節器為例，讀取其NOIM，將不同層之間具有緊固連接關系的零件用實線連接，具有接觸關系的零件用虛線連接，得到如圖5（b）所示的零件分層圖。

　　通過基于同步約束解除的零件分層，可以定位需拆卸目標零件的位置，可知哪些零件可同時拆卸以提高拆卸過程的并行性，提高拆卸效率。

　　2.2 基于子裝配體識別的目標拆卸序列優化

　　2.2.1 關聯零件

　　維修過程中，隨著拆卸任務的不同，拆卸的起點、終點及兩者之間所涉及的零件也會發生變化[8]。針對目標拆卸，本文提出如下定義：

　　定義2.為拆卸目標零件所必須先拆卸的零件稱為目標零件的關聯零件。

　　設零件分層圖共有n層，目標零件r*位于第m層，若零件ri∈[1，m-1]層，且ri與r*接觸，則ri為關聯零件；若ri為關聯零件，ri位于第l層，零件rj∈[1，l-1]層，且rj與ri接觸，則rj為關聯零件；若ri為關聯零件，零件rj與ri同層，且為緊固連接關系，則rj為關聯零件。

　　對裝配體R={r1，r2，…，rn}，目標零件為rm的拆卸任務TASK[rm]，裝配體按與目標零件關聯性分為兩部分：R={R1，R2}。其中R1為關聯零件集合，R2為非關聯零件集合。裝配體關于任務TASK[rm]視為以rm為最終拆卸零件的集合R1的完全拆卸規劃問題。

　　2.2.2 序列優化

　　裝配體通常都包含有子裝配體。識別子裝配體并將其作為整體進行拆卸，對于提高拆卸作業效率具有重要意義。由多個零件組成的部件，判斷其為子裝配體的條件如下：

　　（1）零件數為2，兩零件為緊固連接，且組成零件不包括螺栓等緊固件；

　　（2）零件數大于2但小于零件總數，且組成零件應在分層圖上形成封閉的最小環，同時最外層與最內層零件之間包含緊固連接關系[9-10]；

　　（3）滿足條件（1）或（2）的子裝配體零件集合，如有交集，則合并為一個子裝配體。

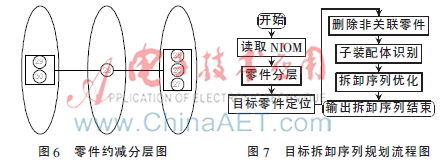
　　依據上述判斷條件，以圖5（a）所示壓力調節器結構為例，可成為子裝配體的組件有：[1，2，6]；[7，8，9]；[22，23，24]；[18，25，26，27]；[29，30]。若排氣閥的活塞皮碗損壞需要更換，根據圖5（b）所示零件分層圖，確定關聯零件為26、27、28、29、30。根據子裝配體條件識別出子裝配體為[25，26，27]；[29，30]。最后生成約減分層圖如圖6所示。要拆卸活塞皮碗25，只需先拆下29、30組成的子裝配體，再拆下28，最后拆下25、26、27組成的子裝配體即可。整個拆卸過程與完全拆卸的過程相比明顯簡化。目標拆卸序列規劃流程圖如圖7所示。

3 實例驗證

　　本文基于三維CAD平臺SolidWorks以及Delphi開發了目標拆卸序列智能規劃系統。系統提取零件的幾何、裝配信息，生成非正交干涉矩陣（NOIM），進行復合拆卸路徑判別，選擇步進次數，并對NOIM進行修正，輸出修正后的NOIM。

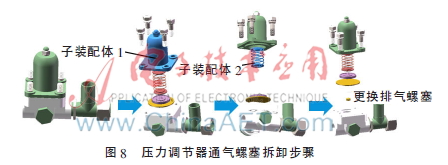
　　讀取NOIM，對零件分層，針對具體維修任務定位目標零件，通過子裝配體優化拆卸序列。圖8所示為壓力調節器通氣螺塞拆卸步驟。

4 結論

　　針對現有方法對于求解復雜裝配零件拆卸路徑誤差較大，解決目標拆卸問題時并行性和效率上存在不足的問題，本文提出較為完善的零件可拆卸性分析與目標拆卸序列規劃方法：

　　（1）結合Vmap投影、非正交干涉矩陣判斷零件初始可拆卸性；對螺紋連接形式進行特殊標記，保證拆卸序列規劃的正確性；將具有初始拆卸方向的零件進行步進干涉檢測直至節點處，應用該方法進行零件復合路徑拆卸判別并對NOIM進行修正。該算法有效解決了復雜裝配零件拆卸路徑求解的問題。

　　（2）采用零件分層圖，定位目標拆卸零件，確定可同時拆卸的零件；劃分關聯與非關聯零件，利用子裝配體識別，去除冗余拆卸步驟，優化目標拆卸序列，提高目標拆卸效率。

　　（3）結合本文零件可拆卸性判別算法和目標拆卸序列規劃方法，基于三維CAD軟件SolidWorks開發了目標拆卸序列智能規劃系統。

參考文獻

　　[1] MARIAN R M ， LUONG L H S， ABHARY K. A genetic algorithm for the optimization of assembly sequences[J]. Computers & Industrial Engineering， 2006，50（4）：503-527.

　　[2] WANG J F ，LIU J H， ZHONG Y F. A novel ant colony algorithm for assembly sequence planning[J]. Advanced Manufacturing Technology，2005，25（11）：1137-1143.

　　[3] 呂風縣，張桂香，張慶紅.基于拆卸和拆卸約束矩陣的裝配序列規劃[J].現代制造工程，2014（1）：21-24，63.

　　[4] 于嘉鵬，王成恩，張聞雷，等.基于優先規則篩選的裝配序列規劃方法[J].東北大學學報，2009，30（11）：1636-1640.

　　[5] WOO T C. Visibility maps and spherical algorithms[J]. Computer-Aided Design， 1994，26（1）：6-12．

　　[6] 于嘉鵬，邢宇飛，王成恩.基于擴展干涉矩陣的幾何可拆卸性判別方法[J].機械工程學報，2011，47（21）：147-156.

　　[7] 趙鴻飛，張琦，王海濤，等.基于同步約束解除的零件爆炸圖自動生成方法[J].中國機械工程，2015，26（1）：70-73.

　　[8] 高檢剛，牟鵬，向東，等.拆卸與或圖模型中的可拆卸性篩子[J].機械設計與研究，2004，20（4）：53-56.

　　[9] 張鶴娜.機遇子裝配體識別和遺傳算法的裝配順序規劃[D].哈爾濱：哈爾濱工程大學，2011.

　　[10] ONG N S，WANG Y C. Automatic subassembly detection from a product model for disassembly sequence generation[J]. The International Journal of Advanced Manufacturing Technology， 1999，15（6）：425-431.