摘 要: 對雙源雙宿兩跳級聯網絡進行了研究,提出了一種TDD模式下可達的網絡容量。首先,考慮一個由三個節點級聯組成的雙源雙宿兩跳網絡模型:首節點是第一信源(S1),其對應信宿為尾節點(D1);尾節點也作為第二信源(S2);中間節點既是S2對應的信宿(D2),也是S1到D1的中繼。網絡工作在時分雙工(TDD)模式,中繼采用解碼轉發(DF)策略。其次,利用最大流-最小割原理獲得了網絡容量的外界,并證明其可達性。對于獲得的容量結論,利用線性規劃數學方法尋找最佳的時隙分配方案,并通過具體實例進行分析驗證。分析表明,調節時隙分配可以優化容量。
關鍵詞: 雙源雙宿;時分雙工;最大流-最小割;容量區域;線性規劃
0 引言
隨著無線通信技術的發展,通信系統的容量成為備受關注的重要特性。容量問題最早源于Shannon在1961年發表的雙向信道的論文[1]。這篇論文中Shannon定義了多址接入信道,隨后Ahlswede對多址接入信道提出了描述[2]。Cover首次提出廣播信道模型,而中繼信道最初是由Van der Mullen針對三終端模型提出的[3]。Mohammad等人[4]針對一般多終端網絡(包括中繼網絡、級聯網絡)研究了可達速率。本文作者分析了分層TDD模式下,多跳無線通信系統的自由度,并針對單源單宿多跳級聯網絡,分別研究了定向和全向傳播兩種模式下的可達速率[5-6],但對于在跳數限制下存在源宿重合和雙向通信的雙源雙宿,以至更一般的多源多宿情況還未提及。
目前學術界對半雙工單源單宿級聯網絡已有豐富的研究成果,但對于多源多宿級聯網絡,研究成果仍比較匱乏。由于全雙工模式自干擾嚴重,實際中為降低成本大多采用半雙工模式。本文考慮采用時分雙工(TDD)通信系統模型,旨在對雙源雙宿兩跳級聯網絡的容量區域進行研究,重點對不同情況下各個網絡狀態的調度問題進行分析討論。
該模型針對最簡單的兩跳級聯網絡,其研究結論是更復雜的多跳網絡的基礎。除了可以用于LTE中繼模式,該模型還可以應用于車輛或船舶組網。例如,在船舶通信領域中,船舶之間通常會組成鏈式隊列展開海上航行。當隊列中船舶之間需要互相傳遞消息時,消息可以從一艘船接力傳遞給下一艘船,處于中間位置的船只需要在準確分離接收自己所需要的消息之后,再將其他的消息向下一艘船只傳遞出去。這種消息的傳遞方式組成一種單源(或多源)對多宿的鏈式級聯通信網絡。
1 系統模型
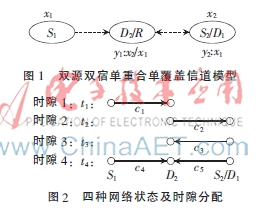
考慮如圖1所示的雙源雙宿單重合單覆蓋信道模型:S1、S2分別代表兩個源節點,D1、D2分別代表對應的兩個宿節點,其中S2和D1節點重合。S1、S2源節點分別有消息x1、x2要發送給宿節點D1、D2。由于是單覆蓋模型,每個節點僅能收到相鄰節點發出的消息。此外TDD模式限制了中間節點不能同時進行接收與發送。因此D2節點在傳輸x1時,將作為中繼節點,接收到x1后采用解碼轉發(DF)策略將x1轉發給目的節點D1。故當所傳消息x1、x2都不為空時,系統完成這兩個消息的傳輸可以由以下四個網絡狀態組成:
狀態1:源節點S1將消息x1發送給D2節點;
狀態2:D2節點將消息x1轉發給宿節點D1;
狀態3:S2節點將消息x2發送給宿節點D2;
狀態4:源節點S1和S2分別將消息x1、x2同時發送給D2節點,即采用多址接入(MAC)模式。
由于采用TDD模式,需要給每個狀態分配對應一段時隙。用tm表示第m個網絡狀態的時隙分配。如圖2所示。
為便于計算消息速率,設上述四個網絡狀態的總傳輸過程在單位時間內完成,共有4個時隙,因此:

每個節點都以滿功率發送消息,進行消息的無差錯傳輸。為使模型更一般化,假設同一鏈路在不同狀態下具有不同的容量。
2 容量區域分析
2.1 網絡信息論基礎
引理1:最大流-最小割定理:在網絡流圖中,任意一個割把網絡中所有節點劃分成兩個集合S和T,其中源點s∈S,匯t∈T,從s到t的最大流量的值等于最小的割的容量。
圖論中的最小割定理最先由Ford和Fulkerson給出。參考文獻[7]中闡述并證明了該定理的可行性。該定理表明在網絡流圖中源節點和宿節點之間的最大流量不大于任何一個分割源和宿的邊集上的和流量,也就是說任何一個邊割集的流量和便是源和宿之間流量的一個上界。
2.2 容量區域
首先分析容量區域的外界。從網絡信息論基礎可知,可利用最大流-最小割定理尋找信息網絡容量的外界。由于模型采用TDD,割集須考慮鏈路激活時間。根據割集定理,可將雙源雙宿兩跳級聯網絡根據其網絡狀態和鏈路狀態進行切割,然后對兩個消息分別進行合并,可得關于兩個消息的速率上界。如下所示:
關于消息x1在第一跳上的割集:
R11≤t1c1+t4c4(2)
關于消息x1在第二跳上的割集:
R12≤t2c2(3)
關于消息x2在第二跳上的割集:
R22≤t3c3+t4c5(4)
根據引理1,源節點和宿節點之間的最大流量等于其中最小的割集容量。故消息x1的可達速率以min(R11,R12)為上界,消息x2的可達速率以R22為上界,消息x1與消息x2的和速率以min(R11,R12)+R22為上界。
綜合以上討論,可得雙源雙宿無線網絡系統的容量區域外界:
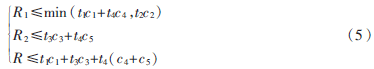
為便于討論,進行以下變量替換。定義 =c2(c4+c5)/(c2+c4),
=c2(c4+c5)/(c2+c4),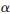 1=c2c4/(c2+c4),
1=c2c4/(c2+c4),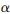 2=c2c5/(c2+c4),則有
2=c2c5/(c2+c4),則有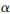 =
=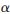 1+
1+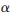 2。對最優時隙分配進行求解,可得容量區域的外界。同時注意到網絡模型中采用無差錯滿速率傳輸,故理論上該外界即是可達的。因此有下面的定理。
2。對最優時隙分配進行求解,可得容量區域的外界。同時注意到網絡模型中采用無差錯滿速率傳輸,故理論上該外界即是可達的。因此有下面的定理。
定理1:雙源雙宿無線網絡系統的容量區域為:
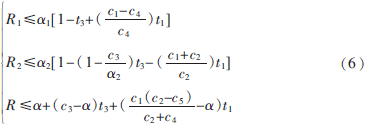
具體表達式將在后面章節給出。下面給出外界中最優時隙分配的證明。
證明:根據式(5)可知,對于消息x1,其速率R1的上界是min(R11,R12)。由于是兩跳中繼,第二跳的速率必然以第一跳的速率為上界;而為了傳輸的穩定性,第一跳傳到中繼節點的所有消息都必須及時被轉發,才能避免消息在中繼節點不斷累積所造成的鏈路擁塞。所以,兩跳鏈路上所傳輸關于消息的信息量應該平衡,即有:
t1c1+t4c4=t2c2(7)
取時隙t1和時隙t3為自由變量,利用平衡式(7)和時間歸一化約束(1)解出:
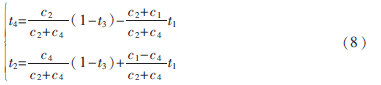
代入容量區域式(5)可得式(6)所示的容量區域外界。具體可達性分析在下一小節中討論。
2.3 容量可達性分析
根據信息論,點對點(PTP)模型最大的消息傳輸速率就是信道容量。Khojastepour[4]提出了多跳TDD級聯網絡的容量為:
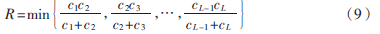
其中{c1,c2,…,cL}是每一跳的鏈路容量。對于兩跳網絡而言,上述公式簡化為:

下面詳細討論R1,R2,R的可達性。
2.3.1 只傳輸x1的情況
假設整個系統僅傳輸消息x1,系統傳輸狀態數目會減少,具體表現為時隙t3和時隙t4對應的傳輸狀態不再存在。
此時R1≤min{t1c1,t2c2},當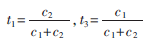 時,R1上界為
時,R1上界為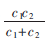 。根據Khojastepour提出的兩跳級聯速率結論(式(10))可知R1能達到上界。
。根據Khojastepour提出的兩跳級聯速率結論(式(10))可知R1能達到上界。
2.3.2 只傳輸x2的情況
假設整個系統僅傳輸消息x2,時隙t3得到全部的傳輸時間。此時根據式(6),R2上界為c3。由于c3正好是點對點的容量,因此R2能達到上界。
2.3.3 消息x1和x2都傳輸的情況
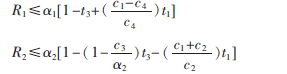
R1、R2同時受到變量t1、t3的影響,可以調節t1、t3使得R最大。具體分析見下節。
3 分析與討論
從容量表達式(6)中可以看出,容量界與系統具體的時隙分配方案有關,因此通過對時隙分配方案進行優化,可以最大化容量的邊界。下面分析該模型在消息x1和x2都傳輸時,如何調度分配自變量時隙t1和時隙t3以使得系統容量上界最大。
3.1 關于總速率R的優化問題
![P2D]3CELUF[CEG7EN3FOJL9.jpg P2D]3CELUF[CEG7EN3FOJL9.jpg](http://files.chinaaet.com/images/2016/02/05/6359029730301700006000622.jpg)
在單位傳輸時間的約束下,上述優化問題可以建模為:
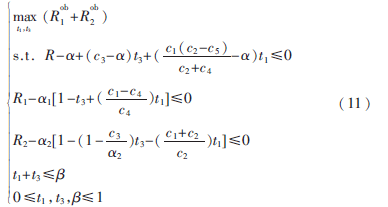
在上述問題中定義了一個時間分配變量![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029743766600004135900.jpg) 它是t1和t3分配到的時間資源加和。這是一個線性規劃問題,可以用圖示法來求解。
它是t1和t3分配到的時間資源加和。這是一個線性規劃問題,可以用圖示法來求解。
根據t1,t3的約束條件可知,約束區域就是線段直線t1+t3=![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029748987000003374096.jpg) 下面區域,由于
下面區域,由于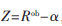 ,求目標函數
,求目標函數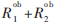 的最大值又可以轉化為先求目標函數Z的最大值,即
的最大值又可以轉化為先求目標函數Z的最大值,即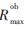
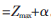 。Z=0的直線為
。Z=0的直線為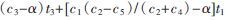 =0,其斜率為
=0,其斜率為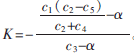 。如圖3所示。
。如圖3所示。
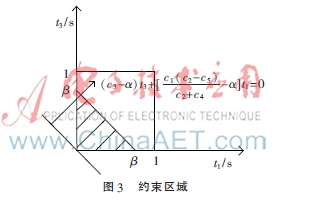
3.2 最優時隙分配的具體分析
此處討論在c3<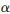 條件下的情況,對于c3>
條件下的情況,對于c3>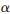 情況類似進行。根據上面問題轉化,先按斜率K與-1的關系討論Zmax最優解。
情況類似進行。根據上面問題轉化,先按斜率K與-1的關系討論Zmax最優解。
3.2.1 Case A:c3>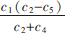
在此情況下直線Z=0的斜率K<-1,Zmax在橫坐標截距點(t1,t3)=(![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029944794500007502541.jpg) ,0)處取得。把此時的t1,t3值帶入
,0)處取得。把此時的t1,t3值帶入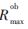
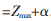 琢表達式得到:
琢表達式得到:
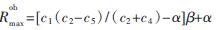
下面結合一個具體網絡實例進行說明。其各跳鏈路容量的選擇應滿足:c1≥c4,c3≥c5,ci≥0,Case A分類條件:c3>c1(c2-c5)/(c2+c4)。此處選擇c1=18,c2=4,c3=3,c4=2,c5=3。
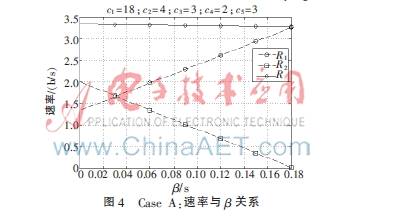
在Case A情況下總速率最大值在橫坐標截距點處取得,時隙3的時間為零,相應的去掉了時隙3,消息x1和x2用剩余三個時隙進行傳輸。變量![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029961591700007944694.jpg) 為時隙1和時隙3的時間和,此時為時隙1的時間分配,調節
為時隙1和時隙3的時間和,此時為時隙1的時間分配,調節![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029964513600005651991.jpg) ,各消息速率隨變量
,各消息速率隨變量![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029963425500008448775.jpg) 的關系如圖4。消息x1需要兩跳傳輸來完成,并且兩跳消息量應該平衡,第二跳所需時間會隨第一跳時間分配
的關系如圖4。消息x1需要兩跳傳輸來完成,并且兩跳消息量應該平衡,第二跳所需時間會隨第一跳時間分配![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029965794500002960981.jpg) 成正比增加,當
成正比增加,當![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029962577200001036002.jpg) 增大到一定值時,為滿足時間總和為單位1,導致t3會為負值,速率R2從而為負。故應對
增大到一定值時,為滿足時間總和為單位1,導致t3會為負值,速率R2從而為負。故應對![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029966586800004946515.jpg) 取值范圍添加約束:
取值范圍添加約束: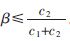 。
。
對于Case A時的雙源雙宿網絡容量區域為:
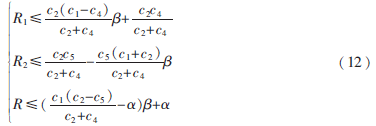
從式(12)可以看出,合理調度時間分配![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029972265900002767129.jpg) ,容量區域與分時(time-sharing)方案相比有所改善(如圖5中由(R1,R2)可達到的散點所構成區域,兩個截距相連以內區域對應為分時方案所得的容量區域)。當
,容量區域與分時(time-sharing)方案相比有所改善(如圖5中由(R1,R2)可達到的散點所構成區域,兩個截距相連以內區域對應為分時方案所得的容量區域)。當![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029971392600003599226.jpg) =0時,容量區域最優。此時,系統省去時隙1和時隙3,在中繼天線數足夠的情況下,僅用時隙2和時隙4即可完成傳輸,而不需要時隙1和時隙3輔助傳輸。
=0時,容量區域最優。此時,系統省去時隙1和時隙3,在中繼天線數足夠的情況下,僅用時隙2和時隙4即可完成傳輸,而不需要時隙1和時隙3輔助傳輸。

上述選取的是c3=c5的情況,對于c3>c5進行容量仿真發現容量區域是沒有改善的,所以case A前提下不適用于c3>c5的情況。

在Case C情況下總速率最大值在縱坐標截距點處取得,時隙1的時間為零,相應的去掉時隙1,消息x1和x2用剩余三個時隙進行傳輸。變量![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029982449900009509446.jpg) 為時隙1和時隙3的時間和,此時為時隙3的時間分配,調節
為時隙1和時隙3的時間和,此時為時隙3的時間分配,調節![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029983455200003071803.jpg) ,各消息速率隨變量
,各消息速率隨變量![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029984302300001484577.jpg) 的關系如圖6。
的關系如圖6。
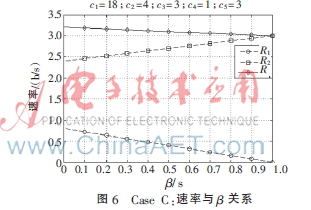
調節![E]$RQECJA78CV$BW0_3MR67.jpg E]$RQECJA78CV$BW0_3MR67.jpg](http://files.chinaaet.com/images/2016/02/05/6359029985284400001819222.jpg) 得到Case C下最優的容量區域如圖7。
得到Case C下最優的容量區域如圖7。
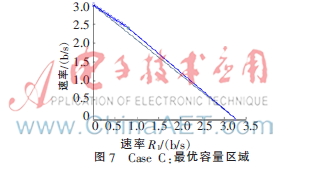
與Case A類似,上述選取c3=c5的情況,對于c3>c5進行容量仿真發現容量區域是有改善的,所以Case C前提下對所有c3≥c5的情況都適用。
4 總結
本文根據最大流-最小割定理研究討論了雙源雙宿兩跳單重合單覆蓋網絡的容量問題。割集定理提供了求解無線通信網絡容量外界的有效方法,利用該方法找到了該模型的容量區域外界,并對其可達性進行了詳細分析。建立了數學優化模型分三種情況分析了時隙的分配調度,進行了實例分析驗證。可以看出,進行合理的時隙調度后的容量區域位于分時傳輸對應的容量區域之上,說明本文提出的處理方案是有效的。本文主要針對的是雙源雙宿的網絡模型,對其研究有助于更一般的多源多宿級聯網絡容量問題的研究。
參考文獻
[1] SHANNON C E. Two-way communication channels[C]. In:Proc.berkeley Symp. math Statist Probab, 1961:611-644.
[2] RUDOFL A. Multi-way communication channels[C]. In Proc. 2nd Int. Symp. Information Theory, Tsahkadsor, Armenian S.S.R,1971:23-52.
[3] MEULEN V D. Three-Terminal communication channels[J].Advances in Applied Probability, 1971(3):120-154.
[4] KHOJASTEPOUR M A, SABHARWAL A. Bounds on achievable rates for general multi-terminal networks with practical constraints[D]. Houston: Rice University, 2003.
[5] LIU F, ZENG L S. Achievable DF rate for cascaded undirected wireless networks with TDD and hidden-terminal[C].Proc. IEEE/CIC International Conference on Communications in China, 2014:643-647.
[6] LIU F, WANG X F, ZENG L S. Fibonacci sequence and cascaded directed relay networks with time- division-duplex constraint[C]. Proc. IEEE International Conference on Communications, Sydney, Australia, 2014:5124-5129.
[7] 盧開澄,盧華明.圖論及其應用[M].北京:清華大學出版社,2005.

