摘 要: 自然通風建筑室內溫度受氣象因素、建筑材料等多種非線性因素的影響,應用機理建模難度較大且計算復雜,很難得到精確的數學模型。利用神經網絡不依賴模型和收斂速度快的優勢和特性,可以很好地解決該問題。本文對經典的BP(Back Propagation)和RBF(Radial-based Function Method)神經網絡建模方法進行對比研究,并對室內溫度進行短期的預測。結果表明,在兩種神經網絡未經過優化的情況下,RBF神經網絡在室內溫度預測的應用要優于BP神經網絡,基于RBF神經網絡的室內溫度預測方法在工程上有廣闊的應用前景。
關鍵詞: 自然通風;室內溫度;神經網絡;預測
0 引言
我國是能源消耗大國,建筑供熱能耗約占社會總資源消耗的四分之一,且隨著大型、高能耗建筑的不斷新建,這一比例還在逐年升高。為了實現建筑節能的目標,必須對建筑室內環境進行準確建模。建筑能量系統是一個非線性、多變量、分布式的復雜系統,在自然通風的條件下,室外氣象因素對室內溫度的影響是非線性的,這使得求解變得復雜[1]。神經網絡為解決上述問題提供了一個可行的方案。人工神經網絡是從微觀結構以及功能上對人腦神經系統進行模擬而建立起來的一類計算模型,能夠模擬人的部分形象思維能力,非常適合非線性預測[2]。目前在工業領域,BP(Back Propagation)和RBF(Radial-based Function Method)神經網絡應用比較廣泛,但在供熱系統中的應用還處于起步階段。因此,本文對這兩種方法分別進行應用,繼而選擇出具有良好應用價值的方法。
1 神經網絡的基本原理
1.1 RBF神經網絡的基本原理
1988年,Moody和Darken提出了一種神經網絡結構,即RBF神經網絡,它屬于前向型神經網絡,一個典型的RBF網絡拓撲結構如圖1所示[3]。

隱層和輸出層的輸入、輸出關系分別為:

其中a1、a2分別為隱層和輸出層的輸出向量;c、σ分別為高斯基函數的中心和寬度;||·||為歐式范數;W為隱層到輸出層的權值矩陣;b為輸出層的閾值向量。由式(1)可知,當輸入信號靠近基函數中心時隱層單元產生較大輸出。
1.2 BP神經網絡的基本原理

BP神經網絡是一種多層的前向型神經網絡。在BP網絡中信號是前向傳播的,而誤差是反向傳播的。一個典型的具有一個隱含層的反向傳播網絡拓撲圖如圖2所示。圖2中,X、Y分別為網絡輸入輸出向量,W1為輸入層和隱層的權值矩陣,W2為隱層和輸出層的權值矩陣,f(X)為隱層激活函數,一般為sigmoid函數,隱層和輸出層的激活函數為purlin線性函數,隱層和輸出層的輸入、輸出關系分別為:
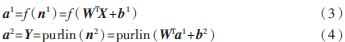
式中,n1,n2分別為隱層和輸出層的輸入向量;a1、a2分別為隱層和輸出層的輸出向量;b1,b2分別為隱層和輸出層的閾值向量。
BP神經網絡采用梯度下降法求連接權值及閾值的變化:
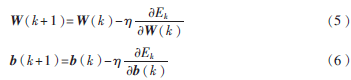
式中,Ek為誤差函數;η為學習效率;W(k+1)、W(k)分別為第k+1和第k步的權值矩陣;b(k+1)和b(k)分別為第k+1和第k步的閾值向量。學習過程是一個反復迭代的過程,當誤差達到預設誤差精度或最大訓練次數時,訓練中止,存儲權值和閾值[4]。
2 神經網絡的建立
對于自然通風的建筑而言,著重分析室內沒有供熱及其他設備散熱以及人體散熱的情況下的室內溫度。在這種情況下,室內溫度因受到室外氣象條件的影響,隨著室外溫度周期性的變化而變化,但是由于建筑圍護結構等蓄熱質的存在,室內溫度的波動相比室外溫度存在一個峰值上的衰減和延遲,其影響因素包括建筑材料、建筑形式、自然通風模式等。在特定的建筑中,建筑蓄熱質可認為是不變的,而氣象因素呈非線性變化。氣象因素包含了室外溫度、太陽輻射強度以及風速等。因此,將室外溫度、太陽輻射、風速作為輸入變量,考慮到上述存在的延遲,將采集時刻也包含在內,室內溫度作為輸出變量。對于RBF與BP神經網絡而言,為了使樣本更適合網絡學習,防止計算過程中出現個別數據溢出的不良現象,需要將各輸入和輸出向量做數據歸一化處理[5]:

網絡學習結束后還需要將得到的0~1之間的預測值反歸一化,這樣就還原成實際值了。
一個具有3層機構的BP神經網絡能夠擬合任意非線性函數,且增加層數并不一定增加網絡的精度,故選取3層BP神經網絡。學習效率定為0.01,誤差精度為10-3,最大訓練次數100。隱含層及神經元的數量的選取對構建BP網絡很重要,目前雖沒有一個權威的結論,但構建過程仍需要先驗知識的輔助。Norihito Kashiwagi等人的研究指出,有限數量的隱含層足以解決非線性和滯后問題[6]。張吉禮在研究了Kolmogorov定理后指出,隱含層節點數應該為2N+1(N為輸入層的節點數)[7]。彭嵐等人發現,第一、第二隱層的最佳節點數應為3∶1[8]。Lippman指出,第二隱層節點數應為2M(M為輸出層節點數)[9]。根據選擇輸入參數,輸入層共有4個節點,隱含層設置為10個節點,輸出層為1。
在RBF網絡中樣本確定后需要確定的參數只有誤差精度和擴展常數(spread)。spread為高斯基函數的分布密度,spread的值越大,需要的神經元越少。隱含層神經元個數的確定同樣是一個關鍵問題,傳統的做法是令其等于輸入向量的個數。本文選取誤差精度為10-3,spread值經過多次調試確定為0.009,建立并訓練網絡。
3 實驗及結果分析
本文以某高校一幢辦公樓為例,室內溫度測試點選在一間南向的房屋內,室外氣象條件由校園氣象臺提供,分別采集室外溫度、太陽輻射強度以及風速,這些數據每隔10 min進行一次存儲。選取5月28日~6月9日中的有效數據1 440條。將這些數據平均分為A、B兩組,一組進行訓練另一組進行測試,如表1和表2所示。

對于RBF與BP神經網絡,首先用A組數據的時間、室外溫度、輻射強度、風速作為輸入量,A組的室內溫度作為目標值進行訓練,訓練結束后獲得建筑室內溫度模型。然后用B組的時間、室外溫度、輻射強度、風速作為輸入量,模型會輸出預測的結果。最后,將模型輸出的預測結果與實際室內溫度值進行對比,得出預測效果。


圖3為BP神經網絡訓練后得到的預測值與實際值曲線圖,圖4為利用RBF神經網絡訓練后得到的預測值與實際值曲線圖,兩者都比較好地實現了對建筑室內溫度的建模和預測。在神經網絡的初期網絡輸出的溫度與實際溫度存在較大差異,但是隨著學習訓練的進行,網絡輸出溫度逐漸趨于實際溫度,誤差有明顯的減小趨勢。從圖5和圖6可見,BP預測絕對誤差最大為4,相對誤差最大不超過0.2;從圖7與圖8可以看到,RBF神經網絡預測的最大絕對誤差為3,相對誤差也不超過 0.15,且兩種預測方法訓練初期絕對誤差和相對誤差都較大,訓練后期誤差有減少的趨勢。從絕對誤差與相對誤差的曲線來看,初期RBF的絕對誤差與相對誤差略小于BP神經網絡,而在后期的訓練過程中BP神經網絡絕對誤差與相對誤差逐漸比RBF小。對比兩者的均方誤差(MSE)可得,BP神經網絡均方誤差為0.43,而RBF的均方誤差為0.48,略高于BP神經網絡。
可以看出,在預測精確度上,BP神經網絡與RBF神經網絡比較接近,二者都滿足建筑室內溫度環境的預測需要。總體來看BP神經網絡的精確度要略微高一些。但是,對于RBF網絡,隱層神經元的最優個數可以在訓練中獲得,而BP網絡要求隱層神經元預先設定,并且最優個數很難確定,同時,RBF每次訓練的結果都很穩定,BP神經網絡每次訓練結果并不同,有時會產生很大偏差,所以在網絡構建方面RBF神經網絡更簡單、方便。
4 結論及展望
本文提出將神經網絡運用于自然通風建筑的室內溫度建模及預測。實驗結果表明,利用室外氣象因素及時間序列對室內溫度進行神經網絡的建模是可行的且效果良好。在神經網絡的構建方面,RBF神經網絡的工作量要比BP網絡小,收斂速度快且泛化能力強,更適用于自然通風建筑的室內溫度建模預測。下一步將搭建Web網絡實驗平臺,利用這一神經網絡模型對自然通風建筑的建筑供熱能耗進行分析和預測,為建筑供熱節能奠定基礎。
參考文獻
[1] 李康吉.建筑室內環境建模、控制與優化及能耗預測[D].杭州:浙江大學,2013.
[2] 周敏,李世玲.廣義回歸神經網絡在非線性系統建模中的應用[J].計算機測量與控制,2007,15(9):1189-1191.
[3] 聞新,周露,王丹力,等.Matlab神經網絡應用設計[M].北京:北京科學出版社,2001.
[4] 魏海坤,徐嗣新,宋文忠.神經網絡的泛化方法[J].自動化學報,2001,27(6):806-813.
[5] 羅新,牛海清,林浩然,等.BP和RBF神經網絡在氣隙擊穿電壓預測中的應用和對比研究[J].電工電能新技術,2013,32(3):110-114.
[6] KASHIWAGI N, TOBI T. Heating and cooling load prediction using neural network system[C]. Proceeding of 1993 International Joint Conference on Neural Networks, Nagoya,Japan, 1993:939-942.
[7] 張吉禮.神經網絡控制原理與工程應用[M].哈爾濱:哈爾濱工業大學出版社,2004.
[8] 彭嵐,何大鵬,李友榮.基于BP神經網絡的工業鍋爐房負荷預測[J].工業加熱,2006,35(5):31-33.
[9] LIPPMAN R P. An introduction to computing with neutral networks[J]. IEEE ASSP Magazine,1987(4):4-32.

