0 引言

    全球定位系統（GPS）被廣泛應用于車載導航領域，當可見衛星數目達到4個或以上時，該系統可以提供連續、精確的導航信息，但GPS信號遮擋會造成定位精度降低。而慣性導航系統（INS）是個獨立運行系統，僅具有短期精度。由于傳感器累積誤差，INS的導航性能會隨著時間的推移而降低。

    為了克服各自系統的不足，現代車載導航系統通常將兩種方法相結合。GPS具有長時精度，因此被用來更新INS位置和速度分量，并抑制INS誤差累計。INS提供精確的短期信息，可以彌補GPS信號遮擋造成的短時間隔。卡爾曼濾波器(KF)是用于隨機模型和先驗知識已知情況下的信息融合算法^[1]，其缺點如下：(1)在低質量傳感器條件下，精確的數學模型難以獲得；(2)車載導航系統和測量設備的先驗信息難以精確確定。

    針對KF的不足，采用基于人工神經網絡(ANN)的方法，從而提高了車載導航系統在GPS信號間隔段內的性能。基于多層感知器(MLP)神經網絡的算法已被應用于戰術級INS^[2]。文獻[2]的研究表明,使用兩個MLP的位置、速度更新架構(PVUA)可以在水平方向上提供準確的位置信息。然而，基于MLP的PVUA系統直接處理INS信息，而不是誤差信息，因此其精度難以被準確評估。此外，MLP算法不能在實時處理中應用。EI-Sheimy提出了基于神經網絡的PVUA算法^[3]，它可以有效擬合非線性系統，相比KF算法該算法具有更優異的性能。Sharaf用徑向基函數(RBF)神經網絡代替MLP^[4]。文獻[3]、文獻[4]中所提兩種方法主要受運算量限制，需要在GPS信號間隔前的所有INS和GPS數據訓練ANN系統。因此，Sharaf和Hiliuta提出了自適應神經模糊推理系統(ANFIS)來實時融合INS和GPS數據^[5，6]。ANFIS算法的不足可能導致巨大的計算負擔。

    此外，低質量的INS受測量噪聲影響，信號主要包括高頻高斯白噪聲分量和低頻INS有用信息。因此，為了減弱INS傳感器噪聲的不良影響，可以應用小波技術去除高頻噪聲^[7]。A.m.hasn提出一種小波算法來分析比較在不同分辨率水平下INS和GPS的輸出^[8]。Tao Zhang提出了一種小波算法來輔助INS、GPS和磁力計組合導航系統中的BP神經網絡^[9]。Sameh給出了依靠小波技術提高INS和GPS導航精度的全面分析^[10]。

    為了優化上述基于ANN算法的性能，本文提出一種基于ANN和小波多尺度分析(WMRA)的新算法。該算法利用RBF神經網絡，實現簡單，訓練快速。當GPS良好工作時，將INS提供的信息作為輸入對ANN進行訓練，并輸出相關誤差信息。小波多分辨率分析被用于降低INS傳感器噪聲，以及在不同的分辨率水平下比較INS和GPS的輸出結果，從而精確訓練ANN。當處于GPS信號間隔時，ANN可以降低INS偏差。因此，相比傳統方法，本文所提方法具有更高的精度。

1 基于EKF和ANN的組合導航方法

1.1 組合導航方法

    基于EKF和ANN的組合導航系統模型如圖1所示。當GPS信號有效時，開關1閉合，開關2斷開，EKF融合INS與GPS的輸出結果進行估計，并給出INS的導航參數誤差。此時ANN把陀螺儀與加速度計的輸出作為其輸入，把EKF的輸出作為其理想輸出進行在線訓練。當GPS信號無效時，開關1斷開，開關2閉合，即EKF不工作，陀螺儀與加速度計的輸出作為已訓練好的神經網絡的輸入來預測INS的導航參數誤差，并對INS輸出的導航信息加以修正。

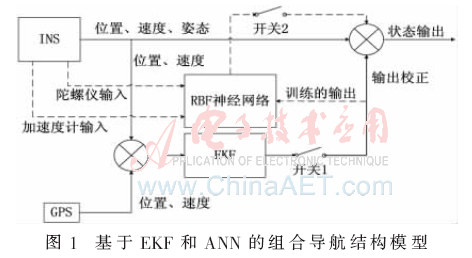
    用EKF估計系統狀態時存在誤差，因此訓練后的ANN不可能嚴格模擬出系統在各種環境條件下的輸出狀態。為了提高ANN的訓練樣本精度，本文采用小波變換方法對導航子系統數據進行預處理。

1.2 基于小波變換的預處理方法

    該方法首先采用小波變換對GPS和INS子系統輸出的導航數據進行高頻去噪，然后進行多尺度分析，獲取相同分辨率下兩者之間的差別，將其作為樣本數據訓練ANN。系統的結構框圖見圖2、圖3。

    如圖2所示，對GPS和INS三個方向上的位置和速度信息進行小波變換去噪，通過比較在相同分辨率下的GPS和INS位置和速度分量，確定精確的位置和速度誤差，并作為樣本數據訓練ANN。如圖3所示，在GPS信號失效時ANN的輸出作為EKF的輸入分量，用來修正INS的導航信息，獲得系統狀態的最優估計。

2 實驗結果性能分析

2.1 實驗設備

    為驗證所提出的車載導航濾波方法有效性，進行了車載實驗。車載實驗使用汽車上裝載的不同性能的GPS和INS設備，包括GPS RTK接收儀器Leica GS10和戰術精度的INS Crossbow的 AHR400CA設備，以及導航精度的INS Honywell的IMU1700設備。

    在車載實驗中，IMU1700和Leica GS10設備構成的組合導航系統，定位精度可在分米級別，用作參考路徑；GPS數據僅使用Leica GS10的偽距定位，與Crossbow低精度設備一起用來測試驗證本算法的有效性。

2.2 車載路線

    車載路線如圖4所示，逆時針方向繞行2圈，每圈約25 min。車載路線被設計為包含GPS無遮擋環境、半遮擋環境和全遮擋環境。其中全遮擋環境下GPS衛星接收數目小于4個。

    在車載實驗的初始階段，汽車來回繞8字形圈進行INS初始化，如圖4箭頭所示，持續大概6 min。其中前3 min的觀測值，用來作為陀螺和加速度計偏差的預測，而初始方向從車載的運行軌跡可粗略推算出。

2.3 車載實驗衛星可見性

    表1為車載實驗過程對GPS間隔進行的統計數據，從表中可以看出實驗過程中會出現GPS間隔（GPS可見衛星數目小于4），這是由于車輛在半遮擋環境或者全遮擋環境下造成的。

2.4 基于EKF和ANN的組合導航結果

    該方法采用ANN的輸出信息提供速度和位置誤差，當出現GPS間隔時可以取代GPS信息進行組合導航。ANN的輸出信息包含四種分量，即位置誤差和速度誤差在南北方向和東西方向的分量。ANN網絡隱層單元數目按照經驗應為3～10之間，具體選取需要考慮訓練誤差和學習步長。

    ANN的訓練學習函數通常是不固定的，根據模型和測量數據選擇最優。本文選取的是Levenberg–Marquardt學習函數。在本次車載實驗中，前400 s是處于GPS可見環境下的，因此用來對ANN進行訓練。擬定訓練步長200以內，誤差小于0.001，經過測試仿真選取隱層單元數目為8。

    為了顯示基于ANN的組合導航性能提升，選取了第4個GPS間隔段內、基于EKF與ANN的導航水平誤差，如圖5所示。第4個GPS間隔持續約為60 s。

    由圖5可以得出，基于EKF和ANN的組合系統精度明顯上升。同一GPS間隔時段內，導航位置最大誤差由12 m縮小到8.5 m。但是車載導航希望更高的導航定位精度，同時GPS和INS子系統輸出導航分量中含有大量高頻噪聲，因此采用小波變換對原始數據預處理。

2.5 采用小波變換預處理方法結果

    小波變換方法對GPS和INS的輸出導航分量去噪，并采用多尺度分析比較兩者的差別，將誤差分量作為輸入供ANN訓練使用。針對上一節同一時段的數據進行仿真分析，得到如圖6所示結果。

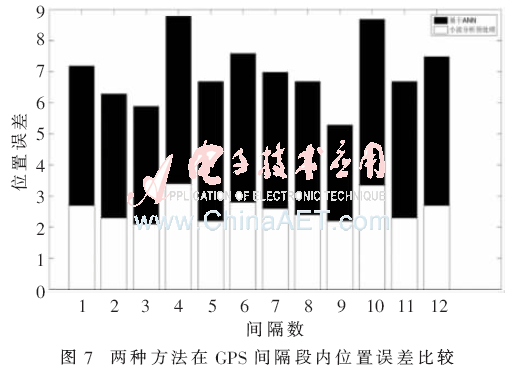
    由圖6可知，通過小波變換預處理后，位置最大誤差小于3.5 m。圖7對基于EKF和ANN的方法與經過小波分析預處理后的方法，在GPS間隔段內的位置誤差進行了比較。可以看出，每個GPS間隔內，經過小波變換預處理后，定位精度有較大提高。3 m以內的定位精度也滿足了車載導航的實際需求，證明了該方法的有效性。

3 總結

    本文將EKF與ANN方法相結合，提出了用于GPS和INS車載組合導航的新方法。當GPS接收機良好運行時，ANN模型被訓練。在GPS信號間隔期間，ANN輸出位置、速度誤差的替代值作為觀測值，顯著地控制了INS誤差的增大。WMRA有效濾出了INS傳感器輸出中的高頻噪聲分量。此外，它還可以在不同分辨率下對INS和GPS輸出分量進行比較。

    對所采用的方法進行了跑車實驗。在GPS信號間隔期間，基于該算法水平最大誤差小于3.5 m，速度最大誤差小于0.5 m/s，導航性能有較明顯的提升，滿足車載導航需求。因此本文所提出方法可以實現無縫銜接的車載導航能力，從而消除GPS信號間隔帶來的影響。

參考文獻

[1] SAADEDDIN K，ABDEL-HAFEZ M F，JARRAH M A.Estimating vehicle state by GPS/IMU fusion with vehicle dynamics[J].Journal of Intelligent & Robotic Systems Theory & Applications，2014，74(1-2)：147-172.

[2] NOURELDIN A，OSMAN A，EL-SHEIMY N.A neuro-wavelet method for multi-sensor system integration for vehicular navigation[J].Measurement Science & Technology，2004，15(2)：404-412(9).

[3] EL-SHEIMY N，CHIANG K，NOURELDIN A.The utilization of artificial neural networks for multisensor system integration in navigation and positioning instruments[J].Instrumentation and Measurement，IEEE Transactions on，2006(5)：1606-1615.

[4] SHARAF R，NOURELDIN A，OSMAN A，et al.Online INS/GPS integration with a radial basis function neural network[J].IEEE Aerospace & Electronic Systems Magazine，2005，20(3)：8-14.

[5] SHARAF R，TARBOUCHI M，EL-SHAFIE A，et al.Real-time implementation of INS/GPS data fusion utilizing adaptive neuro-fuzzy inference system[C].Proceedings of the 2005 National Technical Meeting of The Institute of Navigation，San Diego，CA，2005.

[6] HILIUTA A，LANDRY R，GAGNON F.Fuzzy corrections in a GPS/INS hybrid navigation system[J].Aerospace & Electronic Systems IEEE Transactions on，2004，40(2)：591-600.

[7] 楊麗.遺傳優化小波神經網絡在組合導航中的應用研究[D].南京：南京航空航天大學，2010.

[8] HASAN A M，SAMSUDIN K，RAMLI A R，et al.Comparative study on wavelet filter and thresholding selection for GPS/INS data fusion[J].International Journal of Wavelets Multiresolution & Information Processing，2011，8(3)：457-473.

[9] ZHANG T，XU X.A new method of seamless land navigation for GPS/INS integrated system[J].Measurement，2012，45(4)：691-701.

[10] NASSAR S，ELSHEIMY N.Wavelet analysis for improving INS and INS/DGPS navigation accuracy[J].Journal of Navigation，2005，58(1)：119-134.