0 引言

　　鋰離子電池廣泛應用于國防軍事領域，涵蓋了陸、海、空、天等諸多兵種，攸關信息產業和新能源產業的發展，更成為現代和未來軍事裝備不可缺少的重要能源。然而在其應用領域中仍有許多亟待破解的難題，電池健康狀態（State of Health，SOH）預測[1]就是一個在研究電池使用過程中急需解決的重要問題。

　　健康狀態是指電池從壽命開始到壽命結束期間所處的狀態，它通常以百分比的形式表示，健康狀態也可以被理解為電池經過長期使用后所處的退化程度。健康狀態預測是指根據檢測得到的電池電壓、電流、內阻、溫度等參數，通過一定的算法預測判斷電池所處的健康狀態以及可能出現的故障現象[1]。通過健康狀態預測，可以使得在電池永久損壞前有足夠的時間來采取適當的措施以預防事故的發生。

　　1999年Jaworski就提出用統計參數模型來預測無故障工作時間[2]。Blanke等建立了一種基于阻抗譜的電動/混合動力汽車車載電池容量預測模型[3]。Bhangu等將擴展卡爾曼濾波算法應用于電動車電池的SOH實時預測[4]。Kozlowski提出融合諸如自回歸滑動平均數和神經網絡等數據驅動算法來進行預測和診斷[5]。但當實際工作環境和負載條件與理想數據集不同時通過評估SOH來精確預測電池健康狀態仍然面臨技術難題[6]。為此，本文基于鋰離子電池集總參數模型，提出一種可以融合電池測量數據的狀態估計與預測算法，來實現其健康狀態的精確預測。

1 基于模型的鋰離子電池健康狀態預測流程

　　電池健康狀態的預測可以采用數據驅動、算法模型及兩者綜合的方式實現，此外也可采用電化學模型來描述電池內部動態過程[6]。基于阻容網絡電路仿真實現的動態模型，適用于鉛酸和鎳氫電池，對鋰離子電池而言還需要考慮非線性平衡電勢、放電比率、溫度、熱效應和瞬態功率響應等因素的影響[7]，為此需要測量與電解液比重成函數關系的電壓。

　　基于模型的預測使得產品在使用過程中能夠提早預防，避免事故發生，在汽車、航空和國防工業中已經出現大量的基于模型預測的應用。因為系統模型在早期設計階段已經被仿真，系統的可靠性和魯棒性將獲得最大幅度的提升。這些進展加速了基于模型的系統診斷和預測的一體化，由此產生了一種基于狀態的維護策略，并且提升了系統的可靠性。如果有一個準確的系統仿真模型，診斷和預測就可以與系統設計同時綜合起來。

　　一個系統導向的預測方法需要滿足下列情況[8]：故障檢測和基于檢測的方法能隨著系統元件退化而進行預測，能夠減小任務危險程度和提升決策支持。這種預測不僅能解決個別元件的狀況問題，還能處理這些狀況對任務準備和采取恰當手段的影響。

　　基于模型的預測是假設一個準確的數學模型是存在的，其方法是使用殘差作為特征，殘差是一個實際的系統傳感器測量數據和數學模型輸入之間的一致性檢查的結果。前提是存在故障的情況下殘差很大，在正常的干擾、噪音和仿真誤差的情況下殘差又很小。統計技術用于定義閾值，以檢測存在故障。基于模型的預測過程如圖1所示[8]。

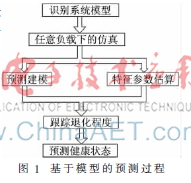
2 鋰離子電池集總參數模型

　　鋰離子電池由一對浸在電解液中的電極組成，化學驅動力來源于兩個電極之間的化學勢能差。例如在室溫20 ℃，1個大氣壓條件下測得理論開路電壓為E0，然而在實際使用過程中實際電壓與E0之間有一個電壓降，這個電壓降主要是由電阻壓降、活性極化、濃差極化三個方面引起的[6]。

　　完全表達內部電化學反應的鋰離子電池模型很難求解計算而且缺少工程實用性。為此，可用近似的集總參數來表達鋰離子電池內部不同因素引起的電壓降，得到如圖2所示的模型[6]。圖中RE表示引起電阻壓降的電解液電阻效應，電荷轉移電阻RCT和并聯的界面電容CDL表示活性極化，RW表示濃差極化。

　　應用集總參數模型在頻域中通過電化學阻抗譜測量方法能做出奈奎斯特圖，并由此更好地理解電池內部的降解過程，但需要特殊的測試設備并且滿足最優測試條件。應用集總參數模型在時域中能得到電池放電曲線，因此可用來對電池健康狀態進行評估和預測。表征電池健康狀態的兩個重要參數是電池的放電終止(End-of-Discharge，EOD)時間和壽命終止(End-of-Life，EOL)點。在此，選擇放電終止時間作為預測參數。

3 基于粒子濾波算法的鋰離子電池健康狀態預測

　　3.1 鋰離子電池健康狀態表征參量

　　放電終止用放電循環中與電荷損耗成函數關系的阻抗參數來表示。隨著電池的放電運行，內部電化學反應和電流流通將使得電池溫度明顯上升[9]，引起電解液離子的活性增加，導致Warburg阻抗RW下降。RW下降一段時間后自放電率將增加，這又會導致產生電解液阻抗RE。而且由于溫度的升高，電池內的反應物消耗速度將加快，特別是在放電循環的末期尤為明顯，這又會引起電荷轉移電阻RCT的增加，并導致電池電壓的突然下降，使電池失去工作能力，如圖3所示。因此EOD可以用如下公式進行計算[6]：

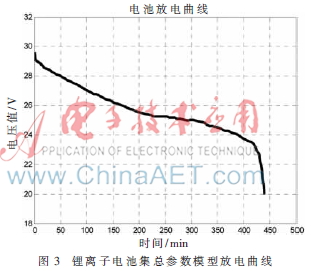
　　其中，Einit是放電循環的初始電壓降，是由測試數據估計出經驗系數。圖3所示為鋰離子電池集總參數模型放電曲線，  能很好地反應出電池電壓隨時間變化的關系，根據它可以預測出電池的放電終止時間。

　　3.2 基于粒子濾波算法的鋰離子電池健康狀態預測

　　公式化模型能用來描述鋰離子電池健康狀態，但有一系列未知參數需要識別，即使從測量數據能得到這些參數也不能直接應用，因為不同電池、同一電池的不同充電循環測得數據都可能不一樣，而且給定循環參數值可能是非穩定的[10]。對于電池健康狀態的預測，必須找到一種能容納非高斯噪聲的非準確、非線性、非穩態模型，粒子濾波提供了一種較為理想的解決方案[2]。

　　3.2.1 粒子濾波算法

　　粒子濾波（Particle Filter，PF）是指通過尋找一組在狀態空間傳播的隨機樣本對概率密度函數（Probability Density Function，PDF）進行近似，以樣本均值代替迭代運算，從而獲得狀態最小方差分布的過程[11]。當樣本數量N→∝時可以逼近任何形式的概率密度分布。與傳統蒙特卡洛方法比較起來，序列重要性采樣使得PF降低了精確預測近似分布所需的樣本數[12]，具有快速性和高的計算效率。

　　PF方法的基本原理是以一系列點來近似條件狀態概率分布p(zk/xk)，這些點被稱之為粒子（來自未知空間的樣本），包含了代表離散概率事件的權重因子[11]。

　　式（6）給出一個描述時間系統的演進非線性過程模型，式（7）是一系列可用的測量數據z1:k=(z1，…，zk)和狀態PDF的初始估計p(x0)。估計過程包括兩個主要步驟：預測和濾波。

　　預測過程用式（8）描述：

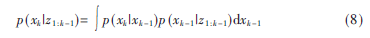
　　濾波環節用現態的觀測值zk和先驗狀態PDF來生成后驗狀態PDF：

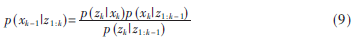
　　其中p(zk|z1:k-1)是規范化因子，與狀態xk獨立。后驗概率密度p(xk|z1:k)無法用解析法求解，這可用如式（11）所示的一系列樣本和第i次采樣相對應的規范化重要性權重因子來近似。

　　其中，重要性函數q(xk|x0:k-1，z1:k)是p(xk|xk-1)的近似估計。

　　3.2.2 EOD預測

　　基于粒子濾波算法的EOD預測狀態轉移方程為：

　　其中，i為時間索引項，fs為采樣頻率，E為在i時刻測得的電壓，wi和vi是相互獨立的高斯噪聲項。

4 實驗及結果分析

　　實驗選擇天津力神電池股份有限公司生產的TBP0306型衛星地面接收站鋰離子蓄電池組，額定容量9 Ah，標稱電壓25.2 V。

　　選定鋰離子電池組放電循環中的電壓變化為研究對象，利用式（12）、（13）作為狀態轉移方程，式（14）作為測量模型，粒子濾波算法估計的電壓平均值和實際輸出電壓曲線如圖4所示。

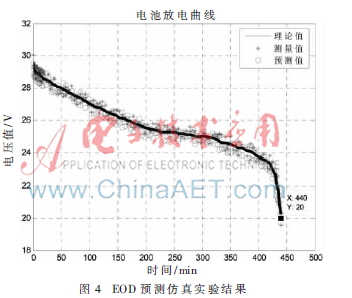
　　圖中曲線“－”表示運用方程（1）計算出的理論放電電壓值；點集“※”表示用測量模型(式14)仿真得到的測量電壓值；點集“○”為用粒子濾波算法預測的電壓值。預測過程仿真實驗中選用與實際環境條件下得到的測量數據近似粒子，粒子數為300，放電曲線計算過程中考慮了高斯噪聲項。通過仿真曲線可以看出，該鋰離子電池組的放電終止時間為440分鐘，即電池組在正常工作條件下可以工作440分左右。經過多次實驗后，對比仿真實驗結果，仿真曲線的一致性較高，殘差在5%之內。

　　從仿真結果可以看出，粒子濾波算法能對鋰離子電池組的放電終止時間給出正確的預測，進而可以預測電池組的健康狀態。

5 結論

　　本文介紹了一種基于模型的系統預測過程，其能預測多種操作模式下的系統剩余壽命。通過對鋰離子電池集總參數模型的分析，提出了利用粒子濾波來預測鋰離子電池的健康狀態參數。選擇放電終止時間作為預測參數，利用粒子濾波算法對鋰離子電池在放電循環中的電壓平均值進行估算并與實際輸出電壓曲線進行比較。數據比較表明，粒子濾波算法能對鋰離子電池健康狀態給出正確的預測。

參考文獻

　　[1] 陳召洪.“鋰想國”探秘：新能源汽車帶來的春之律動[R].萬聯證券新能源研究小組動力鋰電池深度研究報告.2010，09.

　　[2] SAHA B，GOEBEL K，CHRISTOPHERSEN J.Comparison ofprognostic algorithms for estimating remaining useful life of

　　batteries[J].Transactions of the Institute of Measurement and

　　Control，2009，31(3-4)：293-308.

　　[3] BLANKE H，BOHLEN O，BULLER S，et al.Impedance on lead-acidbatteries for state-of-charge，state-of-healthand cranking capability prognosis in elec-tricand hybrid electric vehicles[J].Journal of Power Sources，2005，144(2)：418-25.

　　[4] BHANGU B S，BENTLEY P，STONE D A，et al.Nonlinear observersfor predicting state-of-charge and state-of-health of lead-acid batteries for hybridelectricvehicles [J].IEEE Transactions onVehicular Technology，2005，54(3)：783-94.

　　[5] KOZLOWSKI J D.Electrochemical cellprognostics using fusiontechniques[C].Aerospace Conference 2003，IEEE Proceedings，2003，7：3257-3270.

　　[6] DALAL M，MA J，HE D.Lithium-ion battery life prognostichealth management system using particle filtering framework[J].Proceedings of the Institution of Mechanical Engineers，Part O：Journal of Risk and Reliability，2011，225(1)：81-90.

　　[7] GAO L，LIU S，DOUGAL R A.Dynamic lithium-ion batterymodel forsystem simulation[J].IEEE Transactions on Com-ponents and Packaging Technologies，2002，25(3)：495-505.

　　[8] Luo Jianhui，NAMBURU M，PATTIPATI K，et al.Model-based Prognostic Techniques[C].AUTOTESTCON 2003：330-340.

　　[9] SAHA B，GOEBEL K.Modeling Li-ion battery capacity depletion in a particle filtering framework[C].Annual Conference of the Prognostics and Health Management Society，San Diego，California，2009.

　　[10] 高安同，張金，陳榮剛，等.鋰離子電池荷電狀態估算及剩余壽命預測研究探討[J].電源技術，2014，38(6)：1066-1068.

　　[11] 胡士強，敬忠良.粒子濾波算法綜述[J].控制與決策，2005(04)：262-264.

　　[12] DOUCET D，FREITAS N D，GORDON N.Sequential  Monte Carlo methods in practice[M].Information Science and Statistics，Springer，2001.