文獻標識碼: A
文章編號: 0258-7998(2014)11-0105-04
0 引言
參數化功率譜模型估計方法中基于信號相關函數的自回歸(AR)模型具有多種良好的性能,在理論研究和工程應用中最為廣泛。研究表明,水聲、無線通信等信號常伴有較強的非高斯脈沖噪聲[1-4],?琢穩定分布能夠描述此類脈沖噪聲,在非高斯非線性的信號處理中應用廣泛。針對該類噪聲的特點,參考文獻[1]提出了基于分數低階矩(Fractional Lower Order Moment,FLOM)的共變譜,但是由于方法中待估信號仍需進行二階矩計算,在![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028224341700005745583.jpg) 值接近1時性能下降明顯。參考文獻[2]給出了分數低階協方差(Fractional Lower Order Covariance,FLOC)的方法,克服了譜估計方法的不足。參考文獻[3]提出了分數低階協方差系數,使AR模型系數的估計值收斂能力增強,提高了估計性能,但增加了預設分數低階值的數量,應用中影響了
值接近1時性能下降明顯。參考文獻[2]給出了分數低階協方差(Fractional Lower Order Covariance,FLOC)的方法,克服了譜估計方法的不足。參考文獻[3]提出了分數低階協方差系數,使AR模型系數的估計值收斂能力增強,提高了估計性能,但增加了預設分數低階值的數量,應用中影響了![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028250002500002986610.jpg) 譜估計的精度,對頻率分辨能力影響更大。
譜估計的精度,對頻率分辨能力影響更大。
近年來,相關熵理論[5]的提出為非高斯非線性信號處理帶來了新的思路,基于相關熵的信號處理方法在脈沖噪聲條件下的應用越來越受到重視[4]。相關熵函數是一種新的表征信號局部相似程度的度量形式[6]。由于相關熵對非高斯非線性過程并不敏感,相關熵及由其演化的最大相關熵準則已廣泛應用到多個方面[4-7]。本文將相關熵函數運用到AR模型參數估計中,建立了基于相關熵的AR模型參數估計方法,并通過AR模型參數得到![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028251413500001879511.jpg) 譜估計。本文方法無需預設分數低階值,仿真顯示在相同混合信噪比下能夠在更大的脈沖特性范圍內進行有效的
譜估計。本文方法無需預設分數低階值,仿真顯示在相同混合信噪比下能夠在更大的脈沖特性范圍內進行有效的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028250914300001404027.jpg) 譜估計。
譜估計。
1 ![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027640051300009374214.jpg) 穩定分布噪聲及
穩定分布噪聲及![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027641883200008870133.jpg) 譜
譜
1.1 ![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027640900500003434023.jpg) 穩定分布噪聲
穩定分布噪聲
?琢穩定分布是目前唯一符合廣義中心極限定理的分布類型[1],通常由特征函數進行表征。如果隨機變量?錐存在4個參數(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027642842200006061371.jpg) ,
,![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358027643730900002408327.jpg) ,?酌,a),其中0<
,?酌,a),其中0<![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027644669000004772442.jpg) ≤2,-1≤
≤2,-1≤![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358027645697800005753128.jpg) ≤1,a為實數,其特征函數:
≤1,a為實數,其特征函數:
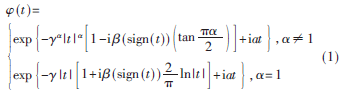
式中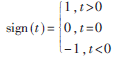 ,則稱X服從?琢穩定分布,記為
,則稱X服從?琢穩定分布,記為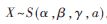 。
。
![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027652197700007733361.jpg) 稱特征指數,表征分布的脈沖特性,值越小分布的拖尾越厚,反之拖尾變薄。稱對稱參數,確定分布的偏斜程度,
稱特征指數,表征分布的脈沖特性,值越小分布的拖尾越厚,反之拖尾變薄。稱對稱參數,確定分布的偏斜程度, =0為對稱分布,稱為對稱
=0為對稱分布,稱為對稱![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358027652881700001143814.jpg) 穩定(S)分布,-1≤<0為左偏斜分布,0<
穩定(S)分布,-1≤<0為左偏斜分布,0< ≤1為右偏斜分布。為分散系數,表征樣本相對于均值的分散程度。a為位置參數,用于確定PDF的位置。
≤1為右偏斜分布。為分散系數,表征樣本相對于均值的分散程度。a為位置參數,用于確定PDF的位置。
除這3種情況外,穩定分布的PDF沒有封閉的表達式。
1.2 S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028228039800001537892.jpg) S分布下的模型
S分布下的模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028228925900008641511.jpg) 譜
譜
S?琢S分布具有很多優良的性質,應用廣泛。隨機過程X(n)的AR模型,可表示為[1]:
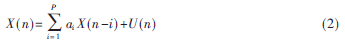
其中ai為AR模型參數,P為模型階數,U(n)~S(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028099599800006520429.jpg) ,0,
,0,![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358028100696500002574643.jpg) ,0)噪聲,如果
,0)噪聲,如果![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028229944000004823258.jpg) 滿足1<
滿足1<![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028230520800009873036.jpg) ≤2,則:
≤2,則:
E[X(n+l)|X(n)]=![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358028231321000008672349.jpg) (l)X(n)(3)
(l)X(n)(3)
其中?姿(l)為X(n+l)與X(n)的共變系數。由式(2)和式(3)可以得到AR模型的廣義Yule-Walker方程:
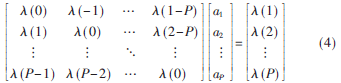
經過推導,S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028104496800009713535.jpg) S分布下的AR模型?琢譜表示為[1]:
S分布下的AR模型?琢譜表示為[1]:
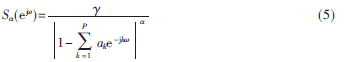
2 基于分數低階統計量的AR模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028232513400003059053.jpg) 譜估計
譜估計
2.1 基于FLOM的AR模型譜![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028107826900001635905.jpg) 估計
估計
基于FLOM的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028108929500001704211.jpg) 譜估計方法是通過隨機過程的共變系數來計算AR模型參數的。X(n)和X(n+l)的共變系數為:
譜估計方法是通過隨機過程的共變系數來計算AR模型參數的。X(n)和X(n+l)的共變系數為:
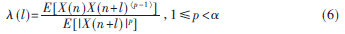
其中x〈p〉=sign(x)|x|p,p為分數低階的階數值。
對于有限的觀測序列X(n),參考文獻[1]給出了共變系數?姿(l)的估計值:
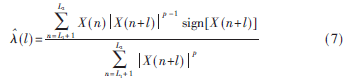
其中L1=max(0,-l),L2=min(N-l,N),l=-P:P(P為AR模型階數),p為分數低階的階數值,N為觀測序列數量。將式(7)代入式(4)可求得AR模型的參數估計值i(i=1,2,…,P)。將i代入式(5)可得不過,該方法不滿足各態遍歷定理,估計精度在較大脈沖條件下下降明顯[3]。
2.2 基于FLOC的AR模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028116032200004749847.jpg) 譜估計
譜估計
由于FLOM方法中共變系數![SK9J]YPKBWJFL9RK72PNLKE.jpg SK9J]YPKBWJFL9RK72PNLKE.jpg](http://files.chinaaet.com/images/2015/10/12/6358028236605400001966171.jpg) (l)具有理論上的局限性,參考文獻[2]提出了兩個S
(l)具有理論上的局限性,參考文獻[2]提出了兩個S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028235439500009365847.jpg) S隨機過程X1(n)與X2(n)之間的FLOC表達式:
S隨機過程X1(n)與X2(n)之間的FLOC表達式:
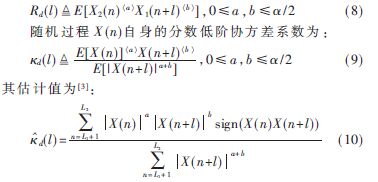
其中L1=max(0,-l),L2=min(N-l,N),l=-P:P,a和b為分數低階的階數值,N為樣本數量。將式(10)的估計值代入式(4)進行求解,即可得到AR模型的參數 i(i=1,2,…,P)。將
i(i=1,2,…,P)。將 i代入式(5)得到AR模型的
i代入式(5)得到AR模型的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028126168400007164781.jpg) 譜估計該方法估計精度得到了很大提高,頻率分辨能力也很強,但是其增加了分數低階取值參數,需對a和b兩個參數進行預先確定,給實際運用帶來不便,且影響估計精度。
譜估計該方法估計精度得到了很大提高,頻率分辨能力也很強,但是其增加了分數低階取值參數,需對a和b兩個參數進行預先確定,給實際運用帶來不便,且影響估計精度。
3 基于相關熵的AR模型![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028128034200003461172.jpg) 譜估計
譜估計
3.1 相關熵函數
Santamaria根據核空間向量的內積定義了一種廣義的相關函數[6](Generalized Correlation Function,GCF),也稱相關熵函數,具有與相關函數相似的性質。
若xt為一個隨機過程,t∈T,則xt的相關熵函數為:

由式(13)可知,相關熵函數包含了隨機變量(xt-xs)所有的偶數階矩,能夠更加準確地刻畫信號特性,同時各偶階矩都受到核尺寸的影響。在實際應用中,核尺寸值常用Silverman準則進行確定。高斯過程的Silverman準則[6]為:
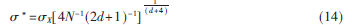
其中,確定的核尺寸值,X為隨機變量樣本的標準偏差,N為樣本數,d為樣本維數。
3.2 基于相關熵的AR模型參數估計
實際有限的信號樣本條件下,離散時間嚴格平穩隨機過程的相關熵函數可估計為[7]:
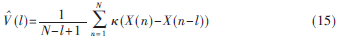
其中,N為樣本個數,?資(·)為高斯核函數,l=-P:P(P為AR模型階數)。同理,將所估計的相關熵函數值(l)代入式(4)得:
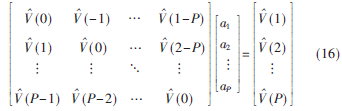
由于相關熵函數具有偶對稱的性質,式(16)左邊相關熵函數矩陣為P×P的正定Toeplitz矩陣[6],求解式(16)可以得到AR模型的參數i(i=1,2,…,P)。將i代入式(5)可得到AR模型的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028208856600005679219.jpg) 譜估。該方法不用預先設置分數低階值,能夠避免因設置的非最優性而對估計精度造成不良的影響。
譜估。該方法不用預先設置分數低階值,能夠避免因設置的非最優性而對估計精度造成不良的影響。
4 仿真實驗與分析
4.1 混合信噪比
在![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028243211600006008906.jpg) 穩定分布噪聲條件下,采用混合信噪比(MSNR)[2]來表示信號與噪聲能量之比:
穩定分布噪聲條件下,采用混合信噪比(MSNR)[2]來表示信號與噪聲能量之比:
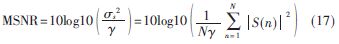
其中?酌為?琢穩定分布噪聲的分散系數,N為信號樣本數,S(n)為有用信號樣本。
4.2 單正弦信號的![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028212722100002120884.jpg) 譜估計性能
譜估計性能
設觀測序列為X(n)=S(n)+U(n)=Acos(2?仔fn)+U(n),n=1,2,…,N。其中S(n)為信號序列,U(n)為噪聲序列,A為信號幅度,f∈(0,0.5)為歸一化頻率,N為觀測序列長度。
U(n)設為標準S![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028217162000005368989.jpg) S分布,特征指數
S分布,特征指數![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028213396400009801325.jpg) =0.5,1.0,1.5,幅度A根據MSNR的取值相應設置,取MSNR=-3 dB,歸一化頻率f1=0.1,AR模型階數P=30。FLOM方法中p=1,FLOC方法中a=0.1,b=
=0.5,1.0,1.5,幅度A根據MSNR的取值相應設置,取MSNR=-3 dB,歸一化頻率f1=0.1,AR模型階數P=30。FLOM方法中p=1,FLOC方法中a=0.1,b=![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028215391300005932507.jpg) /2,而相關熵方法中并不需要提前設定這些參數。為消除信號隨機影響,實驗經過20次蒙特卡洛仿真后取均值。
/2,而相關熵方法中并不需要提前設定這些參數。為消除信號隨機影響,實驗經過20次蒙特卡洛仿真后取均值。
圖1分別給出了FLOM、FLOC和相關熵3種方法的仿真結果。FLOM法在脈沖水平較低時(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028216452600006942911.jpg) =1.5)估計性能良好,能夠準確估計出信號頻率。FLOC方法在中等(
=1.5)估計性能良好,能夠準確估計出信號頻率。FLOC方法在中等(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028214126200003458183.jpg) =1.1)和較低(
=1.1)和較低(![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028214755900008066630.jpg) =1.5)脈沖水平時估計效果均最為優異。本文方法由于對脈沖噪聲不是十分敏感,不僅能夠準確估計出有用信號頻率,而且在各種脈沖特性水平情況下均非常穩定。隨著脈沖特性逐漸提高,FLOM和FLOC法分別在?琢=1.1和?琢=0.5時相繼失效。
=1.5)脈沖水平時估計效果均最為優異。本文方法由于對脈沖噪聲不是十分敏感,不僅能夠準確估計出有用信號頻率,而且在各種脈沖特性水平情況下均非常穩定。隨著脈沖特性逐漸提高,FLOM和FLOC法分別在?琢=1.1和?琢=0.5時相繼失效。
4.3 雙正弦信號![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028217754200004461044.jpg) 譜估計的頻率分辨性能
譜估計的頻率分辨性能
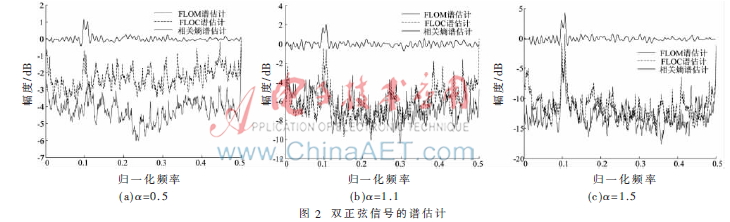
增加一個歸一化頻率為f2=0.11的同幅度信號,即S(n)=A(cos(2?仔f1 n+)+cos(2f2 n)),AR模型階數P=100,MSNR、p、a和b設置同上節,實驗方法不變。圖2分別給出3種![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028219135200009498638.jpg) 譜估計方法對信號頻率的分辨能力。
譜估計方法對信號頻率的分辨能力。![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028221870000002613033.jpg) =1.5時,3種方法均能準確分辨0.01的頻率差;
=1.5時,3種方法均能準確分辨0.01的頻率差;![2B1_YCHR]7PESX2`551D~G9.jpg 2B1_YCHR]7PESX2`551D~G9.jpg](http://files.chinaaet.com/images/2015/10/12/6358028218650700003065430.jpg) =1.1時,FLOM方法失效,FLOC方法性能降低;脈沖特性水平提高到?琢=0.5時,這兩種失效。本文提出方法在三種情況下均能分辨出相鄰兩個信號的頻率,并且頻譜也十分穩定。
=1.1時,FLOM方法失效,FLOC方法性能降低;脈沖特性水平提高到?琢=0.5時,這兩種失效。本文提出方法在三種情況下均能分辨出相鄰兩個信號的頻率,并且頻譜也十分穩定。
5 結論
脈沖噪聲存在于多種信號之中,常規AR譜估計方法性能下降明顯。雖然分數低階矩譜估計方法表現出了良好的性能,但需要提前設置分數低階矩的階值參數,具有一定的盲目性,影響了估計精度,其性能也隨著噪聲脈沖特性水平的提高逐漸下降。相關熵是表征信號間局部相似度的新度量形式,對信號的非高斯特性并不敏感。本文將相關熵函數引入脈沖環境下的AR模型參數估計中,仿真實驗表明,新方法具有不必預設分數低階參數、性能穩健的特點,與基于分數低階統計量的?琢譜估計方法相比,在大脈沖條件下仍能保持良好估計效果。
參考文獻
[1] MIN S,NIKIAS C L.Signal processing with fractional lowerorder moments: stable processes and their applications[J].
[2] XIN Y M,NIKIAS C L.Joint estimation of time delay andfrequency delay in impulsive noise using fractional lowerorder statistics[J].IEEE Transactions on Signal Processing,1996,44(11):1669-2687.
[3] 王首勇,朱曉波,李旭濤,等.基于分數低階協方差的ARSαS模型α譜估計[J].電子學報,2007,35(9):1637-1641.
[4] 邱天爽,張金鳳,宋愛民,等.脈沖噪聲下基于廣義類相關熵的DOA估計新方法[J].信號處理,2012,28(4):463-466.
[5] SANTAMARIA I,POKHAREL P P,PRINCIPE J C.Gener-alized correlation function:definition, properties,and appli-cation to blind equalization[J].IEEE Transactions on SignalProcessing,2006,54(6):2187-2197.
[6] LIU W F,POKHAREL P P,PRINCIPLE J C.Correntropy:a localized similarity measure[C].IJCNN′06.Vancouver,2006:4919-4924.
[7] 袁宵,唐濤,李禹,等.基于相關熵的MACH濾波器[J].國防科技大學學報,2012,34(6):153-157.

