多項式相位信號[1]是具有極低截獲概率的高動態時變信號，屬于非線性調頻信號的范疇，其廣泛應用在通信、雷達、聲納等系統中。二次調頻信號(QFM)是多項式相位信號的特殊情形，其階數為三。二次調頻-偽碼調相(QFM-PRBC)復合信號是一種脈內二次調頻、脈間調相的復合信號，與單一的偽碼調相信號相比，具有更低的截獲概率、更好的抗干擾性能。帶有信息碼的二次調頻-偽碼調相復合信號類似于經過調制的直擴信號，偽碼調相信號為擴頻序列，二次調頻為調制載波。與直擴信號相比，該信號存在于特種通信、抗干擾通信等高動態通信體制中，因此研究這種高動態信號的細微特征具有重要的實際意義。

    目前，國外鮮有對該類復合信號的研究公開。國內主要針對載波是正弦波、線性調頻和正弦調頻的偽碼體制復合信號的參數估計進行研究[2-5],而對于載波是二次調頻信號情形的研究則很少。在實際通信中偽碼序列的估計具有現實意義，對信號的捕獲和追蹤十分重要。雖然帶有信息碼的二次調頻-偽碼調相復合信號類似于直擴信號，但載波調制極其復雜，直擴信號的偽碼估計方法[6]無法有效地估計其偽碼序列，因此本文的重點是研究適合該類復合信號的偽碼盲估計方法。
  
 

　    (5)對搬移后的頻譜V(f)進行IFFT變換，取前半個周期序列經低通濾波器后可得正確的偽碼序列。
　　該算法的實質是通過FFT變換及頻譜搬移抑制一階系數的偏差，從而不會對偽碼估計產生影響。由于選取的任意一段偽碼周期的數據有相應的信息碼，當信息碼為正時，估計的偽碼序列完全正確，信息碼為負時，估計出來的偽碼呈相應的反碼，這并不影響偽碼估計的正確性。
　    由于在步驟(1)中進行的傅里葉變換的長度是偽碼周期長度的兩倍，使得恢復出來的正確偽碼序列的長度是原序列長度的一半，由于偽碼的參數是已知的，可對估計出來的偽碼序列擴展得到原長度的序列波形。步驟(5)中的低通濾波的作用是使恢復出的偽碼波形清晰，便于符號的提取。
3 仿真實驗及其分析
    為了進一步驗證該算法的性能，本文通過使用MATLAB仿真軟件對二次調頻-偽碼調相復合信號的偽碼盲估計過程進行仿真。設接收的信號為采樣后的信號。其中，采樣頻率fs=430 MHz，子脈沖寬度Tp=0.3 μs，子脈沖個數R=7，偽碼周期T2=2.1μs。采樣后的系數為a11=0.15,a22=0.2/m,a33=0.55/m2,m=T2 fs，為一個偽碼周期內的采樣點數。
    實驗1：仿真二、三階系數估計的均方誤差，并對比累加平均次數對系數估計的影響,信噪比范圍為-5~+15 dB，間隔為1 dB，分別進行300次Monte-Carlo仿真。
    圖1、圖2給出了基于累加平均的三次相位函數來估計二、三階系數的性能曲線。圖1是a22的估計性能，從中可看出，當累加平均的次數為10時，均方誤差在-1 dB時達到最小，且隨著信噪比的增大，均方誤差保持不變；當累加平均的次數為20時，均方誤差在-2 dB時達到最小，可見適當增大累加平均的次數可改善估計性能，該特性在圖2中也清楚地反映出來。圖2是a33的估計性能，從中可以看出隨著信噪比的增大，均方誤差呈遞減趨勢，當信噪比大于5 dB時遞減趨勢趨于緩慢，且經過累加平均處理的均方誤差小于未累加的。

    實驗2：對降階后的正弦波與偽碼調相復合信號進行偽碼的估計，其中不考慮估計系數偏差的影響，并且仿真不同子脈沖個數及信號長度對偽碼估計性能的影響，其中數據是經過300次Monte-Carlo仿真的平均結果。
    圖3給出了信噪比為2 dB時，經過低通濾波后恢復出來的偽碼序列波形。從圖中可以看出，恢復出來的偽碼序列與原序列相比，符號完全相同，只是長度減為原序列的一半，此時該偽碼周期對應的信息碼為正，當信息碼為負時，估計的偽碼序列呈反碼，這是由信息碼的符號影響的。由于恢復偽碼時采用了低通濾波器，使得恢復出來的偽碼波形的幅值呈現微小波動，但不影響符號的判定，通過下采樣及取符號可得偽隨機二進序列為{-1,1,-1,1,-1,-1,1}。

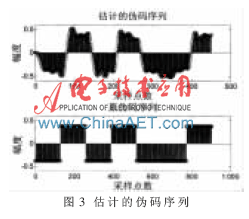
    圖4是在其他參數不變而子脈沖個數為7和15時的性能曲線，其中正確估計率是指偽碼完全估計正確的次數與總次數之比。從圖中可以看出,隨著信噪比的增大，偽碼估計的正確率逐漸增大；在同一信噪比下，子脈沖個數為15的正確率要遠大于子脈沖為7的正確率，比如信噪比為0 dB時，其正確估計率為0.877 1高于7個子脈沖的0.558 3。為了達到相同的估計性能，子脈沖個數為15的抗噪性能比7個的提高了約8 dB，由此可見當子脈沖個數為15時具有更好的估計性能。

　圖5顯示了在子脈沖個數為15的條件下不同采樣頻率對偽碼估計性能的影響(即信號長度的影響)。從圖中可以看出在同一信噪比下，采樣頻率越大，則信號長度越長，偽碼估計的正確率越高，且采樣頻率大的具有更好的抗噪性能。
    本文針對二次調頻-偽碼調相復合信號的偽碼盲估計問題進行討論，采用基于累加平均的三次相位函數估計二次調頻的二、三階系數，利用估計系數重構指數項，其與原復合信號相乘可實現降階。降階后的信號取實部可得正弦波與偽碼調相的復合信號，通過頻譜搬移的方法可恢復偽碼序列。仿真驗證了該算法的可行性與有效性，其結果表明，15個子脈沖的估計性能優于7個子脈沖，在SNR≥1 dB時，偽碼估計的正確率大于0.9，且適當增大采樣頻率可提高偽碼的估計性能。本文所提的偽碼盲估計算法為該類高動態復合信號的捕獲與追蹤奠定了基礎。
    由于該方法中間步驟較多，存在誤差傳播，且未考慮系數估計的偏差對偽碼估計的影響，后期將圍繞這方面深入研究，以便進一步提高偽碼估計的性能。
參考文獻
[1] PELEG S, PORAT B.Estimation and classification of polynomial-phase signals[J]. IEEE Transactions on Information Theory,1991,37(2):422-430.
[2] 熊剛，趙惠昌，林俊.偽碼-載波調頻偵察信號識別的譜相關方法(I)：偽碼-載波調頻信號的譜相關函數[J].電子與信息學報，2005,27(7): 1081-1086．
[3] 熊剛，趙惠昌，王李軍.偽碼-載波調頻偵察信號識別的譜相關方法(II)：偽碼-載波調頻信號的調制識別和參數估計[J].電子與信息學報，2005,27(7): 1087-1092．
[4] 熊剛，楊小牛，趙惠昌.基于平滑偽Wigner分布的偽碼與線性調頻復合偵察信號參數估計[J].電子與信息學報，2008,30(9):2115-2119．
[5] 張淑寧，趙惠昌，黃光明. 基于ZAM分布的偽碼調相與正弦調頻復合引信信號特征參數提取技術[J].宇航學報，2008，29(6):1965-1969.
[6] 張天騏，張傳武，林孝康，等. 直擴信號偽碼周期及序列的估計算法[J].系統工程與電子技術，2005,27(8):1365-1368.
[7] 田日才. 擴頻通信[M].第1版. 北京:清華大學出版社，2007.
[8] SHIMON P, BENJAMIN F. The discrete polynomial-phase transform[J]. IEEETransactions on Signal Processing,1995,43(8):1901-1914.
[9] O’SHEA P. A fast algorithm for estimating the parameters of a quadratic FM signal[J]. IEEE Transactions on Signal Processing, 2004,52(2):385-393.
[10] Wang Pu, Yang Jianyu, DJUROVIC I. Alg-orithm extension of cubic phase function for esti-mating quadratic FM  signal[C]. Acoustics, Speechand Signal Processing. Honolulu: ICASSP,2007:III-1125-III-1128.
[11] 何丹娜，張天騏，高春霞，等. 線性調頻-偽碼調相復合信號的偽碼盲估計新算法[J]. 電訊技術，2012, 52(6):906-912.