文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.175067
中文引用格式: 蘇艷,羊梅君. 用于秩虧MIMO系統的球形譯碼器研究[J].電子技術應用,2018,44(8):102-104.
英文引用格式: Su Yan,Yang Meijun. Research on sphere decoders for rank-deficient MIMO systems[J]. Application of Electronic Technique,2018,44(8):102-104.
0 引言
多輸入多輸出(MIMO)是無線通信中最有前景的技術之一,但是MIMO系統中的檢測實際上是很耗時的。最大似然(ML)搜索方法是十分耗時的,尤其是對于大天線陣而言[1]。迫零(ZF)[2]和最小均方誤差(MMSE)檢測器[3]相對不那么復雜,但性能較差。盡管球形譯碼器(SD)可簡化ML檢測,SD的平均復雜度仍然成指數級[4]。這種情況對于秩虧MIMO系統甚至更糟。固定復雜度球形譯碼器(FSD)[5]能夠將可變SD復雜度修復成可接受的階數,同時保持類似于ML的性能,因此備受關注。
傳統的FSD(FSD-ZF)遵循的是由預處理算法所決定的搜索順序。它將搜索分為兩個階段:FE階段位于前面p層,SE階段位于剩下的NT-p層。它有以下兩個缺陷:(1)如果NR<NT,FSD-ZF的誤比特率(BER)性能將嚴重變差;(2)FE階段中每層信號元素的選擇有賴于選定信號本身的后處理效果。本文將會討論適用于不同天線配置的FSD,并提出一新的RFSD算法(RFSD-s)。
1 MIMO通信系統模型
本文考慮的MIMO系統模型是在接收端有NR根天線、發射端有NT根天線的V-BLAST系統[6]。x為發射端發射信號向量,向量中的符號分別獨立取自M-QAM的星座點。接收端接收信號向量y由下式得出:

式中,w是復高斯白噪聲向量,H表示頻率平坦衰落信道。
2 穩健的固定復雜度球形譯碼器(RFSD-s)
2.1 沒有噪聲時的RFSD:RFSD-ZF

情況2:NT≤NR。在這種情況中,對FE階段的深度p沒有限制。因此,對任意整數p≥1,情況1中的算法同樣可使用。只要p≥NT-NR,那么RFSD-ZF便對天線的配置具有魯棒性。
2.2 簡化的RFSD-ZF:SRFSD-ZF

2.3 帶有噪聲信息的穩健FSD:FSD-MMSE
通過歸一化MMSE可得傳輸信號x的估計值如下:

式中,(Gi)j表示矩陣Gi的第j行。運行FSD-MMSE可以簡單地認為是可進行平行處理的擴展版MMSE-OSIC。MMSE既適用于NT≤NR,也適用于NT>NR。
3 仿真結果
RFSD-s的BER性能和復雜度可以通過對不同星座大小和MIMO配置進行仿真。
3.1 NT=NR的獨立MIMO信道
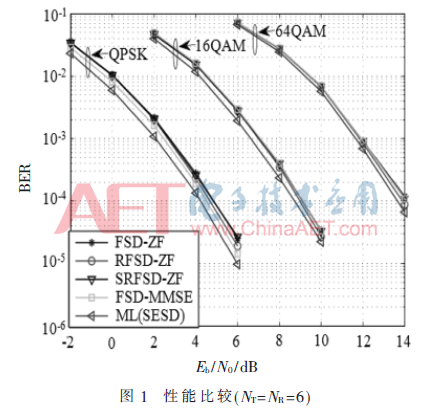
圖1表示的是模擬一6×6系統,分別使用了QPSK、16QAM和64QAM調制,都遵循擴展策略(1,1,1,1,1,M)得出不同Eb/N0下RFSD-s的BER性能。ML檢測是通過Schnorr-Euchner球形譯碼(SESD)實現的。(1,1,1,1,1,M)表明RFSD-s和FSD-ZF在FE階段(p=1)的M-QAM星座中擁有M種搜索路徑。可以觀察到RFSD-s和FSD-ZF都表現出幾乎準ML性能,尤其是大星座下。RFSD-ZF和FSD-MMSE的BER性能都略優于FSD-ZF。
3.2 NT>NR的獨立MIMO信道
圖2為模擬一4×5(NR×NT)系統,分別使用QPSK、16QAM和64QAM調制,RFSD-s與SESD[7]的BER性能比較。圖2中的BER性能提升是很顯著的。FSD-ZF和RFSD-s都遵循擴展策略(1,1,1,1,1,M)。在這種情況下,FSD-ZF的性能下降,RFSD-s仍然有準ML性能。

3.3 復雜度比較
在獨立信道中傳輸16QAM信號的4×5系統中,分別考慮實值加法/減法和實值乘法/除法。對于包含預處理的每個檢測算法來說,用于檢測復符號的平均浮點運算數量如圖3所示。FSD-ZF和RFSD-s都遵循擴展策略(1,1,1,1,16)。從圖中可以看到RFSD-s的復雜度遠低于SESD。盡管RFSD-s的復雜度略高于FSD-ZF,但FSD-ZF的BER性能顯著下降。SRFSD-ZF極大地減小了RFSD-ZF的復雜度,同時保留了較佳的BER性能。

4 結論
本文提出了用于秩虧MIMO系統的RFSD-s算法。相比較于SD和傳統的FSD,本文提出的RFSD-s具有兩個優勢:固定復雜度和穩健。在NT>NR和NT≤NR兩種情況下,RFSD-s能夠具有準ML性能,且復雜度更低、更固定。對于沒有或有噪聲信息的情況,分別提出RFSD-ZF和FSD-MMSE。針對不同情況進行了仿真(如不同調制方案和天線配置),驗證了算法的有效性。
參考文獻
[1] 魏利霞.MIMO系統的信號檢測算法研究[D].南京:南京郵電大學,2015.
[2] 薛宸.多活躍天線空間調制技術的低復雜度檢測算法[J].電子技術應用,2015,41(8):73-75.
[3] 郭鳴霄,徐鵬飛,王瑞山.MIMO系統的信號檢測算法分析[J].電子科技,2016,29(3): 65-67.
[4] JALDEN J,OTTERSTEN B.On the complexity of sphere decoding in digital communications[J].IEEE Trans.Signal Process.,2005,53(4):1474-1484.
[5] BARBERO L G,THOMPSON J S.Fixing the complexity of the sphere decoder for MIMO detection[J].IEEE Transactions on Wireless Commun.,2008,7(6):2131-2142.
[6] 唐元元,張德民,劉哲哲,等.TD-LTE系統中軟輸出球形譯碼檢測算法研究[J].電子技術應用,2012,38(11):55-58.
[7] CUI T,TELLAMBURA C.An efficient generalized sphere decoder for rank-deficient MIMO systems[J].IEEE Communications Letters,2005,9(5):423-425.
作者信息:
蘇 艷,羊梅君
(華南理工大學廣州學院 電子信息工程學院,廣東 廣州510800)

