宋海聲，呂耕耕，劉岸果

　　（西北師范大學 物理與電子工程學院，甘肅 蘭州 730070）

       摘要：提出了一種新算法，有效地減少了最近鄰域法和貪婪算法在構建旅行商問題可行解過程中引入不合理長邊的問題。該算法先借助一種由偽凸包算子所得到的分層模型對旅行商問題中的城市分布進行分析，之后通過將分層模型中相對外層的點逐個添加到內層的規則得到可行解。借助仿真實驗求解TSPLIB標準庫中的40實例，并與最近鄰域法和貪婪算法進行對比，結果表明分層融合算法具有更高的精度，其平均求解質量達到8.47%。

　　關鍵詞：旅行商問題；偽凸包；分層模型；分層融合算法

　　中圖分類號：TP301.6文獻標識碼：ADOI： 10.19358/j.issn.1674-7720.2017.06.005

　　引用格式：宋海聲，呂耕耕，劉岸果. 一種基于分層模型的TSP構建算法［J］.微型機與應用，2017,36（6）：13-15，21.

0引言

　　*基金項目：甘肅省自然科學基金（1606RJZA065）旅行商問題（Traveling Salesman Problem, TSP）是在1954年由美國學者Dantzig［1］提出的，是已被證明的NPHard組合優化問題［2］。由于其在郵遞員投遞路線選擇、生產作業排序VLSI芯片設計、電路板鉆孔、機器人控制、X光設備定位、電子地圖和計算機網絡等眾多領域有廣泛應用價值，因此近些年來產生了大量的關于TSP的文獻。其中大多數文獻主要集中于啟發式算法的研究，可以分為構建型和以構建型為基礎的改進型兩類。比較常見的改進型算法有遺傳算法［3］、蟻群算法［4］、粒子群算法［5］、免疫算法［6］、模擬退火算法［7］、禁忌搜索算法［8］等，其求解質量高，速度比較慢；而構建型算法具有簡潔、求解速度快的特點。經典的構建算法有最近鄰域法（the Nearest Neighborhood Algorithm, NN）［9］、貪婪算法（Greedy Algorithm, GA）［10］、插入法［9］等。

　　由于最近鄰域法、貪婪算法和插入算法的構建結果中均含有不合理的長邊，因此本文在繼承最近鄰域法、貪婪算法的思想后，通過建立分層模型來規避這一問題，提出了分層融合算法（Hierarchical Fusion Algorithm, HFA）。通過實驗求解TSPLIB標準庫中的40實例并與NN和GA算法進行對比，結果表明本文算法求解TSP具有更高的精度。

1TSP的描述

　　TSP可以描述為：在目標城市個數和任意兩城市之間距離都已知的情況下，求解一條遍歷所有城市一次且僅一次并返回到起點城市的最短線路。該問題可以用如下的數學模型描述：

　　設N表示城市個數，D表示距離矩陣，dij表示兩城市間的距離，Inf為一足夠大的正數,i，j為下標表示城市，Tour表示線路的集合,Tp(l)表示線路Tp中的第l個城市，Len(Tp)為線路Tp總長度，那么有：

　　顯然，使得Len(Tp)取得最小值的線路Tp就是TSP的最優解。根據不同的劃分標準TSP大致可以分為三類：

　　（1）按距離矩陣是否為對稱矩陣，分為對稱TSP和非對稱TSP；

　　（2）按任意3個城市間距離值是否滿足三角不等式，分為三角不等式TSP和非三角不等式TSP；

　　（3）按城市的坐標位置是否完全符合歐幾里得平面規則（兩城市之間的距離可以通過坐標計算得出），分為歐幾里得TSP和非歐幾里得TSP。本文在未加聲明時的TSP均為歐幾里得TSP。

2分層融合算法

　　2.1分層模型

　　分層模型是指將問題的處理過程分解為多個具有結構相似性或功能獨立性的過程。建立分層模型可以讓問題的描述變得簡單，并使得問題的求解過程更具條理性。本文針對TSP建立分層模型并提出以下假設：

　　（1）使用坐標點表示城市的位置，且所有的城市都分布在二維平面上；

　　（2）不存在具有相同坐標的兩個點，若坐標相同則按一個點處理；

　　（3）任意一個點，不能同時出現在兩個不同的層中；

　　（4）各個層必須采用相同的方式得到。

　　2.2偽凸包算子

　　本文采用偽凸包算子得到的偽凸包結構進行分層模型的建立，其步驟如下：

　　（1）找出剩余城市的坐標矩陣tempX和剩余城市的個數ccity，按照剩余城市的橫坐標從小到大的排序得到剩余城市在橫坐標方向的排序xsq；

　　(2)當ccity<4時，返回xsq和ccity,否則，執行步驟(3)；

　　(3)按照剩余城市的縱坐標從小到大地排序得到剩余城市在縱坐標方向的排序ysq并取得端點西west=xsq(1)，東east=xsq(ccity)，南south=ysq(1)，北north=ysq(ccity)；

　　（4）初始化層layer=zero(1,N),層中城市個數cl=0；

　　(5)從西到北取得縱坐標增大的點并添加到layer中，更新cl；

　　(6)從東到北取得縱坐標增大的點并反向添加到layer中，更新cl；

　　(7)從東到南添加縱坐標減小且未曾添加到layer中的點到layer中，更新cl；

　　(8)從西到南取得縱坐標增大且未曾添加到layer中的點并反向添加到layer中，更新cl，返回layer和cl。

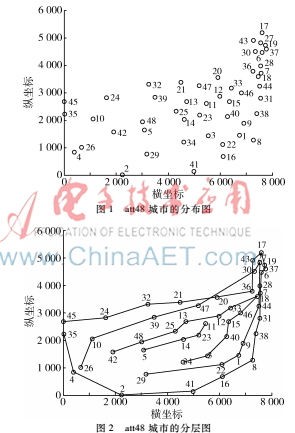
　　圖1是TSPLIB標準庫中att48城市的分布圖。圖2為分層模型所得到的att48城市分層圖，其中每一條多段線表示一個層。

　　2.3分層融合算法求解TSP

　　本文提出的分層融合算法建立在分層模型基礎之上，采用偽凸包算子得到TSP的分層模型，之后將分層模型中相對外層的城市加入到相對內層的層中完成融合。其中融合過程只限于兩層之間并且是從最內層向最外層進行的。分層融合算法求解TSP的過程可以分為兩個階段：第一階段使用偽凸包算子進行分層模型的構建；第二階段將得到的分層模型按照融合規則進行融合求出構造解。

　　第一階段：得到分層模型。

　　(1)初始化城市個數N，剩余城市的集合CITY=1:N，剩余城市個數ccity=N，城市坐標矩陣X。

　　(2)如果ccity>0，創建層記錄矩陣xLayers=zeros(ccity,N)并令層個數clayers=0，跳到步驟(3)；否則，提示錯誤。

　　(3)當ccity>0時，重復執行步驟(4)；否則返回分層模型矩陣Layers=xLayers(1:clayers,:)。

　　（4）采用偽凸包算子得到一層，更新剩余城市的集合CITY，ccity，clayers++。

　　第二階段：對分層模型進行融合。

　　（1）初始化得到第一階段所生成的分層模型矩陣Layers和層個數clayers。

　　（2）當clayers>1時；重復執行步驟（3）；否則，返回Layers(1,:)。

　　（3）分取得相對內層inlayer=Layers(clayer,:)和相對外層outlayer=Layers(clayer-1,:)，利用融合規則算子將兩層融合并將得到的結果賦給Layers(clayer-1,:)。

　　其中步驟（3）中所用到的融合規則算子詳細步驟如下：

　　①取得相對內層inlayer、相對外層outlayer、outlayer中城市的個數coutlayer以及inlayer中城市的個數cinlayer。

　　②當coutlayer>0時，重復執行步驟②；否則，返回inlayer。

　　③隨機從outlayer中選擇一個點作為將要添加的點addpoint。

　　④當cinlayer<3時，neighbourhood=inlayer;否則，從inlayer中選擇2個距離addpoint最近的點的集合作為neighbourhood。

　　⑤計算addpoint分別插入到neighbourhood中兩點兩側時的距離增量，將addpoint插入到距離增量最小的位置，coutlayer--，更新inlayer。

3算法測試

　　實驗求解了TSPLIB標準庫中的40個實例，通過比較NN、GA與HFA三種算法的求解質量，對算法的性能進行了測試。實驗平臺為MATLAB 7.10.0（R2010a），CPU為AMD A83500M，內存為2.0 GB，主頻為1.5 GHz。三種算法求解TSP實例的結果對比表如表1所示。其中實例名稱指的是TSP的名稱和該問題所包含的城市個數；最優路徑長度指的是實例已知的最優路徑長度；平均解和最優解分別指的是平均求解質量和最優求解質量，計算方法為：（解得路徑長度/最優路徑長度-1）*100%。需要注意的是，GA為確定算法，每次求出的結果都相同，所以只求解一次；而NN和HFA為不確定算法，所以進行了多次實驗。當城市個數n≤100時，進行n次求解；當100<n≤1 000時，進行100次求解；當n>1 000時，進行50次求解。

　　由表1可知，在求解質量上NN的平均求解質量最差，為26.02%；NN的最優求解質量和GA的求解質量相當，為18%左右；本文提出的分層融合算法求解質量明顯優于NN和GA。其平均求解質量和平均最優求解質量的均值分別為8.47%和4.99%，說明算法的魯棒性和求解質量同時得到提高，相對于GR+MVODM的性能更好［11］。

4結論

　　本文針對旅行商問題提出了分層融合算法，借助分層模型從整體入手有效避免了經典構造算法后期引入長邊的問題，從新的方向給出了旅行商問題構造解方式。該算法的優點在于求解質量高，建立了可重復使用的分層模型；不足之處在于偽凸包算子構建的層模型過于單一，各層之間進行融合時鄰域制約了構造解的多樣性。

參考文獻

　　［1］ DANTZIG G, JOHNSON S. Solution of a largescale travelingsalesman problem［J］. Operations Research, 1954, 2(4):393410.

　　［2］ GAREY M R, JOHNSON D S. Computers and intractability: a guide to the theory of NPcompleteness［M］.W.H. Freeman and Company， 1979.