熊濤
(南京郵電大學 自動化學院，江蘇 南京 210023)
摘要：基于非自治級聯系統理論，以非完整移動機器人為研究對象，研究多剛體系統的一致性問題，提出了一種新的分布式控制器。通過引入持續激勵擾動項，驗證了無論參考信號是否為持續激勵信號，所提出的控制器都能實現系統一致性的目的，且能一致到期望的參考值。利用李雅普諾夫方法對系統進行了穩定性分析。最后，對所提控制器進行數值仿真，結果驗證了所提出的控制器的有效性。
關鍵詞：非自治級聯系統；多剛體系統；持續激勵；非完整移動機器人
0引言
多剛體系統的一致性控制在多機器人合作控制、交通車輛控制、無人機編隊和網絡資源分配等領域有著廣泛的應用。多剛體系統姿態同步的控制方法主要包括：主從式控制法、基于行為的控制法以及虛擬結構控制法。文獻［1］中，WANG P K和HADAEGH F Y提出了主從式（LeaderFollower）控制法，該控制方法將同步問題轉化為一般的跟蹤問題，優點是可以單獨分析某個剛體的跟蹤性能，而缺點是一旦Leader發生故障或失效，其他剛體將失去參考信號，無法完成同步目標，造成系統混亂。文獻［1］作為該領域的開創性成果，研究了多領導者情況下的多剛體姿態協調控制，運用了近鄰控制器的概念，使系統達到了全局漸近穩定。BALCH T和ARKIN R C提出了基于行為（Behaviourbased）的控制法［2］，根據相鄰剛體的姿態變化來調整自身的變化，優點是某個剛體的故障或失效并不會影響到整個剛體群的運動，而只是影響相鄰剛體的運動。文獻［3］憑借局部信息交換，設計有效的控制律，解決了一隊剛體的姿態對齊問題。 REN W和BEARD R W提出了虛擬結構（Virtual Structure）控制法［4］，假設剛體群中存在虛擬的單個剛體，每個剛體都根據該虛擬剛體調整自身的姿態。文獻［4］中提出的集中式虛擬結構法使剛體群依賴于唯一的虛擬剛體，容易使其成為單個失效點，而文獻［5-7］提出的分布式虛擬結構法則避免了該缺點。因此，后來的姿態同步問題多運用分布式控制法。本文針對平面二維多剛體系統，基于圖論、非自治級聯系統理論和非線性系統穩定性理論等方法，對多剛體系統的一致性控制問題進行探討。
符號說明:令R表示實數集合，Rn表示n維實數列向量集合，Rm×n表示m×n實數矩陣集合，xT表示實數向量x的轉置，diag{x1,x2,…,xN}表示對角元素為x1,x2,…,xN的對角矩陣，IN表示N階單位矩陣，G表示圖。
1問題描述
本文以非完整移動機器人為研究對象，考慮由N個具有相同機械結構的非完整移動機器人組成的系統，運動方程由以下方程組表示：
其中，i=1,2,…,N。當i=d時，表示移動機器人組的期望參考軌跡，ud、ωd是已知的時變函數。根據相關圖論知識，這N個移動機器人可以表示為圖G=(V,E)的N個節點。通過輸入和狀態的轉化，系統(1)可被轉化為如下級聯形式：
其中，xi1=θi，xi2=xi，xi3=yi，ui1=ωi，ui2=uicosθi。當i=d時，表示參考機器人方程的級聯形式。
根據上述系統模型，控制目標可以概括為：對于每一個追隨者，基于其本身及其鄰居的狀態，設計一個控制器，使系統中的機器人狀態達到一致，且都一致于期望狀態。但是在實際情況中，由于外部干擾、通信時延等因素的影響，要達到理想的一致是比較困難的，因此，實際的控制目標為：在合適的控制器和通信拓撲下，系統 (1) 中所有機器人的狀態收斂到期望值的一個鄰域內，即對系統(2)設計控制律使得：
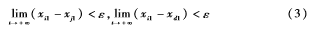
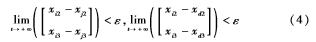
其中，i，j=1,2,…,N，ε是一個大于0的常數，代表誤差范圍。
系統(1)寫成矩陣形式為：
根據李代數相關秩的條件［8］，很容易證明系統 (5) 是可控的。然而，一個無漂移常規系統光滑穩定的必要條件是系統輸入的數量等于狀態的數量，因此，找不到靜態光滑或連續的反饋控制器來穩定系統 (1) 。查閱文獻［9］可知，運用線性時不變連續狀態反饋可以實現系統的一致性。本節接下來將會研究已知期望參考軌跡的多剛體系統的一致性問題。
2控制律設計
基于前述級聯系統的形式及前期工作中已有的控制律：
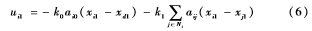
其中，k0>0,k1>0是正常數，aij是系統通信拓撲結構圖的鄰接矩陣的元素，aij=1表示剛體i可以接收剛體j的狀態信息，ai0=1表示剛體i可以接收參考剛體的狀態信息；相反地，aij=0和ai0=0表示剛體i和剛體j以及參考剛體之間沒有通信，無法得知它們的狀態信息。
結合協調控制律ui2：
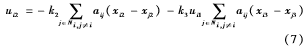
其中，k2>0，k3>0是正常數。
通過仿真研究可以看到，所有狀態無法都達到一致，這說明基于積分器系統或線性系統的一致性結果不能直接沿用到非完整移動機器人系統中。基于此，本文針對兩種不同期望的參考信號重新設計了控制律。
定義1［10］：存在正常數α1、α2和δ使以下不等式對所有t>0成立：
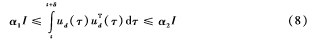
則稱ud為持續激勵。
(1)控制律ui1的設計
當ud1是持續激勵信號時，顯然，系統(1)的所有狀態都是可控的。仍然采用控制器(6)來控制(1)的第一個子系統。
當ud1→0（或甚至ud1=0）時，首先定義剛體i與其鄰居之間的平均距離為：
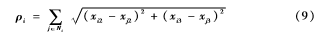
構造控制律ui1如下：
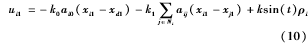
(2)控制律ui2的設計
首先，定義矩陣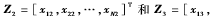
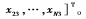,…基于非完整移動機器人系統控制方面的研究結果，無論ui1收斂到持續激勵信號或者是零，構造如下控制律：
其中，L∈Rn×n是系統無向連通圖的Laplacian矩陣。
從公式(11)的結構可以看出，如果ud1→0（或甚至ud1=0），那么所有xi1達到一致的速度快于Z2和Z3的一致速度，所以狀態xi3將達不到一致。但由于控制律ui1設計時引入的持續激勵擾動項ksin(t)，使系統保持可控，此時，運用所提出的控制律ui2可以使所有狀態變量都達到一致。
3穩定性分析
定理1如果φ(t)是一個持久激勵信號，k2>0和k3>0是常數，且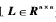
是系統無向連通圖的Laplacian矩陣，那么系統：
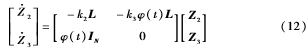
將達到指數一致。
證明：考慮無向圖G的Laplacian勢能相關函數作為Lyapunov函數：
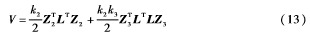
當G是連通圖時，上式為半正定，對其求導得：
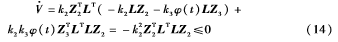
可以看出，其導數為負半定。
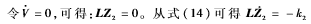
由于φ(t)是持續激勵信號，因此易得到LZ3=0。所以，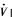
的最大不變集為：
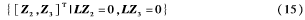
根據LaSalle不變集原理以及穩定性理論，［Z2,Z3］T指數收斂到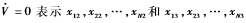
將達到指數一致。
定理2(當ud1是持續激勵信號時的一致性定理)假設系統通信拓撲結構是無向連通的，且至少有一個剛體能接收參考信號xd1的信息，則系統(1)在控制器(8)和(13)的控制下能達到一致。
證明：在控制器(6) 和(11)的控制下，閉環系統可以寫成如下形式：
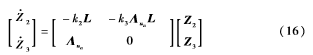
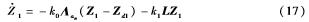
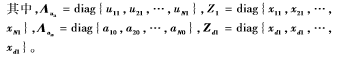
將系統(16)中的ui1用ud1來替代，則系統(16)可視作系統：
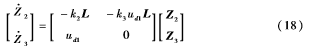
被
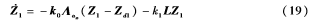
級聯，級聯項為：
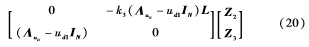
(1)如果系統的通信拓撲結構是連通的，且至少有一個剛體可以接收參考信號系統(2)的信息，則子系統將指數一致到ud1。
(2)根據定理1，當ud1是持續激勵信號時，子系統(18)將達到指數一致。
(3)級聯項(20)滿足［Z2,Z3］T的線性增長條件。
那么，基于以上3個條件，并根據非自治級聯系統的理論［10-12］，系統的通信拓撲結構是聯通的，且至少有一個剛體可以接收參考信號時，系統中的N個剛體在控制器(6)和(11)的控制下能夠達到期望的一致。
定理3（當ud1→0（或ud1=0）時的一致性定理）假設系統通信拓撲是無向連通的，且至少有一個剛體能接收xd1的信息，則系統(1)在控制器(10)和(11)的控制下達到一致。
證明:
(1)當ρi≥ε時
這種情況下，在控制器ui1的設計中引入持久激勵信號來保證整個系統的可控性，例如控制器(10)中的ksin(t)。對于子系統(19)，在連通通信拓撲結構下，ui1將收斂到ksin(t)。對于子系統，在控制器(10)的控制下，根據非自治系統的級聯理論，以及φ(t)=ksin(t)時定理1的指數一致結果，可得出ρi<ε。
(2)當ρi<ε時
在這種情況下，系統的通信拓撲結構是連通的，且至少有一個剛體能接收參考信號，當ρi在ε領域內自由取值時，系統(19)能收斂到原始的參考信號。那么，在控制器(10)和(11)控制下，多剛體系統的實際一致性問題得到解決。
基于定理2和定理3，通過證明可知，在重新設計的控制器中，無論ud1是否是持續激勵信號，多剛體系統都能達到一致性。
4仿真結果
本節將所提出的控制器與前期工作所設計的控制器進行比較。在現有的控制律(6)和(7)下，基于無向連通拓撲結構，k0=1,k1=1,k2=5,k3=6。從圖1中可以看到，無法讓第三個狀態達到一致。
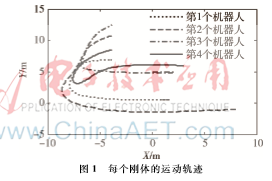
由于參考信號趨于零的情況下非完整移動機器人系統的一致性研究較少，為了闡述本文所提出的控制器的有效性，以下將進行兩種不同參考信號的仿真。
（1）ud1=0
選取系數：k0=1,k1=1,k2=5,k3=6，誤差范圍為：ε=0.000 01。系統初始狀態為：
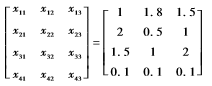
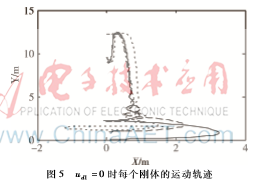
基于定理3中提出的一致性協議，仿真結果顯示如圖2~圖5，從圖中可以看到，每個機器人狀態都能達到一致。
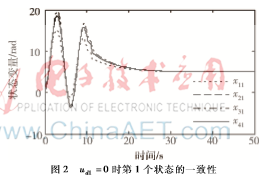
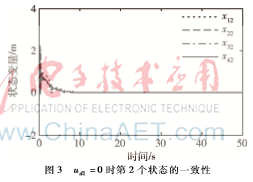
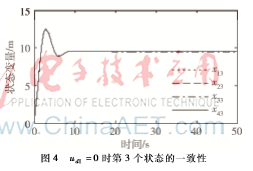
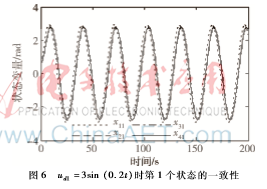
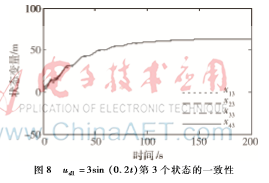
（2）ud1=3sin (0.2t)
這種情況下，參考信號為一個持久曲線信號，取k0=8,k1=1,k2=5,k3=6，系統初始狀態為：
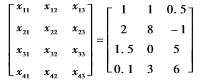
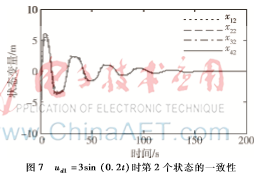
仿真結果如圖6~圖9，基于定理2中的一致性協議，仿真結果表明每個剛體都能達到一致，從運動軌跡圖中可以看到，所有的剛體最后都收斂到一起，并呈一定的曲線運動，從仿真圖中可以看出本文所提控制器能有效實現系統一致性。
5結論
本文利用非自治級聯系統理論，提出了一種具備無論系統參考信號是否為持續激勵信號都能實現系統一致性的分布式控制器。該控制器的設計通過在控制律中引入持續激勵擾動項，改善了前期工作的缺點，在參考信號不為持續激勵信號時，也能讓系統達到一致性。最后，將所提控制方法應用到兩種不同參考信號的情況中，仿真結果驗證了所提出的控制方法的有效性。
參考文獻
［1］ WANG P K C,HADAEGH F Y. Coordination and control of multiple microspacecraft moving in formation ［J］. Journal of the Astronautical Sciences, 1996, 44(3): 315-355.
［2］ BALCH T,ARKIN R C. Behavior based formation control for multirobot teams ［J］. IEEE Transactions on Robotics and Automation, 1998, 14(6): 926-939.
［3］ Ren Wei. Distributed attitude alignment in spacecraft formation flying ［J］. International Journal of Adaptive Control and Signal Processing, 2007, 21(23): 95-113.
［4］ Ren Wei, BEARD R W. Virtual structure based spacecraft formation control with formation feedback ［C］. AIAA Guidance, Navigation, and Control Conference and Exhibit. 2002: 2002-4963.
［5］ Ren Wei, BEARD R W. Decentralized scheme for spacecraft formation flying via the virtual structure approach ［J］. Journal of Guidance, Control, and Dynamics, 2004, 27(1): 73-82.
［6］ Zou Anmin, KUMAR K D, Hou Zengguang. Attitude coordination control for a group of spacecraft without velocity measurements ［J］. IEEE Transactions on Control Systems Technology, 2012, 20(5): 1160-1174.
［7］ ABDESSAMEUD A, TAYEBI A, POLUSHIN I G. Attitude synchronization of multiple rigid bodies with communication delays ［J］. IEEE Transactions on Automatic Control, 2012, 57(9): 2405-2411.
［8］ ISIDORI A. Nonlinear control systems ［M］. Springer Science & Business Media, 1995.
［9］ Dong Wenjie, FARRELL J A. Cooperative control of multiple nonholonomic mobile agents ［J］. IEEE Transactions on Automatic Control, 2008, 53(6): 1434-1448.
［10］ Zhou Jiakang,Ma Guangfu, Hu Qinglei, et al. Delay depending decentralized adaptive attitude synchronization tracking control of spacecraft formation［J］. Chinese Journal of Aeronautics, 2012, 25(3): 406-415.
［11］ PANTELEY E, LORIA A. On global uniform asymptotic stability of nonlinear time varying systems in cascade ［J］. Systems & Control Letters, 1998, 33(2): 131-138.
［12］ 齊玉峰. 非線性級聯系統的穩定性分析及控制設計［D］. 天津:天津工業大學, 2006.