馬方超

　　（同濟大學 電子與信息工程學院， 上海 201804）

　　摘要：在進行集成電路系統的仿真時，如何加快含有互連線寄生效應所產生的延時信息的計算變得尤為重要。采用模型降階的方式對具有互連線寄生效應的電路系統系數矩陣進行降階，以達到加快含有互連線延時信息的互連電路仿真速度的目的。通過泰勒級數展開的高階逼近技術，將傳遞函數中的e－sτ項進行多項式展開逼近，而后采用高階Arnoldi算法進行降階，所以降階算法繼承了傳統矩匹配算法的保持無源性和結構性的優點，又能保證一定的精確度。算法最初的目標降階數采用Hankel奇異值決定，減少了降階的迭代次數，大大縮減了計算時間。

　　關鍵詞：互連線寄生效應；泰勒級數展開；高階逼近；矩匹配

0引言

　　集成電路是整個信息產業發展的基礎,而電子設計自動化(EDA)則是支持集成電路高速發展的支柱。在早期的小規模電路中，互連線的尺寸遠小于信號波長，相對于門上時延，互連線的時延很小可以忽略不計。但隨著工藝的不斷進步，互連線尺寸逐漸縮小，電路工作頻率進入GHz水平，使得互連線寄生效應也越來越明顯，互連線的時延與門上時延更加接近，因此互連線的時延已經不可忽略。

　　常見的互連線寄生效應主要由趨膚效應、襯底效應和串擾等組成。為了精確描述互連線寄生效應，一般采用寄生參數提取的方式，即獲取互連線的等效模型及其等效參數。本文電路模型針對互連線寄生效應中的趨膚效應采用部分元等效電路(PEEC)的方法對趨膚效應進行分析，完成互連線寄生電阻與寄生電感的參數提取。模型還會考慮互連線與襯底間的電容耦合效應，互連線間的串擾和襯底損耗等因素，使得互連線等效電路模型更加精確。對于大規模集成電路中的互連線而言，寄生參數提取之后的電路仿真需要求解的電路節點數會達到千萬以上的量級，如果使用傳統的Spice進行仿真則時間過長。因此在計算含時間延遲的電路模型時引入模型降階的思想，以達到簡化電路模型從而大大加快計算速度的目的。

　　模型降階方法是分析互連線電路的有效方法之一［1］。模型降階中比較成熟的一類算法是基于矩匹配的算法，例如傳統的SPRIM算法［2］，其通過塊Arnoldi降階的方式在保證了系統無源性的前提下更能完全地保證電路系統的結構性，使得模型降階算法在實際中加快電路仿真速度有了現實意義。針對互連線寄生效應所帶來的互連線延時問題，本文將傳統的矩匹配降階算法改進為更加適合計算處理該種含有互連線時延信息的電路系統的仿真算法。

1互連線電路模型

　　因為要滿足制造工藝原則，芯片內部的互連線實質上是一條條具有不同長度、厚度和寬度的導線［3］。在現實研究仿真中，由于工作在高頻中的互連線的寄生效應（如趨膚效應、串擾等）越來越顯著，如何快速地建立一種高速精確的互連線模型成為集成電路仿真中的首要工作。

　　1.1PEEC模型

　　對于一個雙互連線模型［4］,在考慮到互連線的趨膚效應與襯底損耗兩種情況下，本文給出與實際情況非常接近的PEEC模型。PEEC模型是基于PEEC法的等效電路模型，PEEC法通過對互連線單元切割的方式，能夠精確計算在趨膚效應影響下的互連線自身的寄生電阻Rs與寄生電感Ls。將襯底效應與襯底損耗、線間串擾等因素一起考慮到等效電路中，可以得到等效模型如圖1所示。其中Csub與Rsub為襯底電性損耗模擬，Cox1與Cox2為互聯線與襯底形成的電容等效，Cm為線間串擾。

　　1.2PEEC模型延時計算

　　本文采用Elmore方法對互連線延時τ進行計算，因為采用PEEC提取的電路模型實質上是RLC樹狀模型（不考慮襯底損耗對延時造成的影響）。此時：

　　τ=2t=2(1.047e－ξ0.85+1.39ξ)/ω

　　其中ζ為阻尼參數，ξ=12RCRL，ω為臨界頻率，ω=1LC。

2降階算法推導

　　通過泰勒級數展開的方式，將傳遞函數中含有的e－sτi項進行展開逼近，而后采用高階Arnoldi算法實現降階。因此降階后的矩陣擁有了SPRIM降階算法的保持無源性和結構性的優點，又確保了很好的精確度。又因為算法最開始通過對hankel矩陣奇異值進行分析求取初始最優降階數，減少了降階算法的迭代次數，大大加快了計算速度。

　　2.1傳遞函數轉化

　　對于一個含有k個τj時延的n維p口電路網絡，其傳遞函數為［5］：

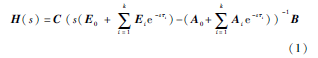
　　與不含延時計算的常規電路系統的傳遞函數相比，加入互連線本身延時計算的傳遞函數增加了∑ki=1Eie－sτi和∑ki=1Aie－sτi兩部分，其中這兩部分中的Ei和Ai對應的是引入延時部分的位置信息，是含有非零元素極少的稀疏矩陣，而e－sτi部分反映的是該延時部分的延時大小。本文使用泰勒級數展開，通過對e－sτi進行多項式展開之后取高階逼近，使傳遞函數轉化為不含e－sτi項的形式。

　　2.2零階逼近

　　在s域中將e－sτi在s=0處泰勒級數展開：

　　系統的hankel奇異值為：σi=λi(RL)。當σR<<σR+1時，選取r0=R為初始最優目標降階數。

　　2.3高階逼近

　　對e－sτi進行r階逼近時有：

　　矩陣降階過程如下：

　　令G=m0－1B,Lj=m0－1mj，K0=G

　　可以得到：K1=L1K0，K2=L1K1+L2K0，…，Kr=∑rj=1(LjKr－j)。

　　令：K=［K0,K1,K2,…,Kr］,可以得到其r階的Krylov 子空間為［6］:

　　Kq(L1,…,Lr,G)≡colsp(K)(4)

　　由給定的Krylov子空間(4)和最優降階數r求得降階矩陣Xk：

　　colsp(Xk)=Kq(L1,...,Lr,G)

　　通過降階矩陣Xk對傳遞函數中的系數矩陣進行降階：

3實驗仿真驗證

　　本文實驗采用兩條并行的單位長度的金屬線，等效為一個2×2的PEEC模型，如圖2所示，每條互連線由20段PEEC單元等效模型組成，其中CL是負載電容。

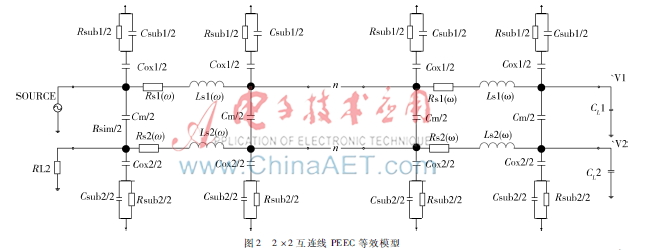
　　使用hankel奇異值的方法求得初始最優降階數為14，經迭代后求得最終最優目標降階數為16。使用本文提出的降階算法以及傳統降階算法與降階前傳遞函數的頻域響應對比，如圖3所示。不同方法對應的電路仿真的CPU運行時間對比如表1。

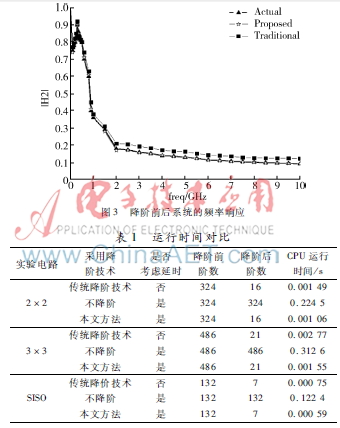
　　由圖3可以看出在頻域上，本文提出的降階算法降階前后頻率響應幾乎一致,圖中表現為三角形曲線與五角星圖3降階前后系統的頻率響應曲線幾乎完全重合。改進后的降階算法與傳統的降階算法相比，在處理含有時延信息的計算上更為精確。由表1可以看出，采用本文所提出的算法，在電路仿真速度上提高了近200倍。

參考文獻

　　［1］ 蔣耀林.模型降階方法［M］.北京：科學出版社， 2010.

　　［2］ FREUND R W. SPRIM: structurepreserving reducedorder interconnect macromodeling［C］. In IEEE/ACM International Conference on Computer Aided Design, 2004: 8087.

　　［3］ 揚帆.集成電路分析中的模型降階方法研究［D］.上海：復旦大學，2008.