摘? 要: 針對基-2 FFT處理算法,采用分塊存儲思想,將存儲器、處理機數據交換網絡模型進行優化。優化后的網絡模型數據通路數僅為20,降低為原來的4%以下,且不隨FFT計算點數增多而增加。整個設計在Virtex系統芯片XCV800上實現。?
??? 關鍵詞: 實時信號處理;并行計算;FFT;網絡模型?
?
??? 實時信號處理系統[1]廣泛應用于圖像處理、語音處理、智能儀表、通信以及自動控制等領域。FFT/DFT作為數字信號處理(DSP)系統中常用的積分變換算法被普遍使用。同時FFT運算的計算量很大,往往構成實時信號處理的計算瓶頸。本文以空間太陽望遠鏡的相關跟蹤系統為研究背景[2],考慮我國可應用到航天環境的高可靠性的電子系統其主頻往往不高于25MHz,所以采用并行計算的策略。通過對計算資源與速度的平衡分析,選擇在FPGA內構造兩個蝶形處理器實現并行計算。兩個處理機采用共享存儲器模式[3]。如果在存儲數據與處理機之間采用傳統數據總線方式,需要總線仲裁器對總線的請求進行分時應答,難以實現數據從源節點到目標節點的實時傳輸;而采用點對點任意連接的網狀結構會使設計復雜度大幅增加。因此,本文針對FFT運算特點,設計了存儲器與并行機的網絡模型。該網絡模型沒有數據傳輸延遲,但結構得到了極大簡化。?
1 并行FFT結構分析?
??? 本文針對32×32點序列的圖像進行FFT變換。可以采用行列變換的形式,對于每行/列數據可以用基-2算法[4]進行計算。基-2算法計算的核心為蝶形運算。為了實現并行處理,在FPGA內部構造出兩個蝶形運算模塊,結構如圖1。?
?
?
??? 圖1中RAM為FPGA塊存儲器,存放原始數據和FFT之后的最終結果。“Base-2 Core”為蝶形運算單元,圖中為兩個蝶形運算單元并列構成雙核結構,其中每個蝶形運算單元的輸入和輸出都是兩個數據通道。Input Buffer是存儲器與蝶形運算單元之間的數據緩存,它逐行接收從存儲器RAM發來的數據,然后按一定順序發送給兩個處理單元,并緩存中間結果。Output Buffer為輸出緩存,它將FFT最后一級的計算結果進行緩存,等待主存儲器RAM空閑時再發送過去。?
2 處理機與存儲器網絡模型?
??? 雙核處理器的數據輸入和輸出都是4個通道,每個通道均為復數形式的18位浮點數據(共計36位寬度)。4個通道同時工作意味著有相對應的4個并行的存儲器通道。而輸入序列是存儲在輸入緩存中的兩行/列共64點數據。如果輸入緩存采用FPGA內部的Block Ram方式實現,則難以實現4個通道同時工作。因為32點的基-2FFT共分5級運算,每一級運算請求的數據順序不同,即使構造4端口的存儲器也無法實現同時讀取任意4個數據。如果用FPGA內部的查找表(LUT,Look Up Table)實現分布式存儲,則存儲器與雙核處理器組成的網絡結構如圖2。?
?
?
??? 圖2中上方的圓形區域代表存儲的數據,下方的圓形區域代表雙核處理器的4個通道。如果每個數據都可能進入雙核處理器的每一個輸入端,則數據通路如同圖2的網絡結構。假設上方的數據點數為M,下方的數據通路為N,則連接復雜度計算公式為:?
????
?
其中,P為通路個數,不同方向表示不同的通路,即公式中的系數2。對于本文情況,數據點M為64,計算通路N為4,所以連接復雜度為512。?
3 基于PN算子的網絡模型簡化?
??? 在基于FFT的蝶形運算中,并非所有數據都有進入任何數據通道的可能性,而是按照一定的規律順序進入4個計算通道。根據并行FFT算法,并行FFT可以表示為如下遞歸形式[5]:?
????
?
其中,xi為第i級變換;C為和差算子;
為旋轉因子的乘積運算;PN為完全混合算子。其中C和的作用是完成蝶形運算,而PN的作用是將數據進行重排。因此可以根據數據重排規律進行網絡優化。?
??? PN算子的作用是將序列(a,b,c,d)轉化為序列(a,c,b,d)。假設輸入序列和輸出序列均轉化為二維形式:?
????
?
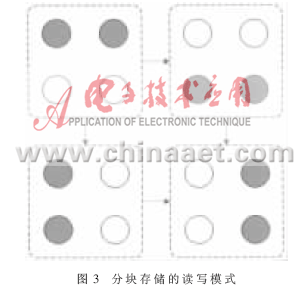
??? 這樣完全混合算子的作用相當于矩陣的轉置。因此設計上既不采用FPGA內部Block Ram設計輸入緩存,也不用分布式存儲方法,而是利用分塊存儲的方式。假設將存儲器分為4塊,則基于完全混合算子的數據讀寫方式如圖3所示。?
?
?
??? 圖3中圓形區域表示存儲的分塊,4個存儲區域構成一個緩存整體。為了實現矩陣的轉置,將讀和寫的控制分開,讀取序列為上半區和下半區,寫入序列為左半區和右半區。圖中實心圓形為活動存儲單元,空心圓形為非活動存儲單元。圖中上兩個矩形分別代表讀取的兩種模式,下兩個矩形則代表寫入的兩種模式。通過讀取和寫入的不同實現了序列的轉置。圖3中同時只有兩個存儲區域活動代表雙核處理器的一個計算單元,即兩個計算通道。另外兩個計算通道情況相同。基于以上設計模型,實際的數據連接模型如圖4。
?
?
??? 圖4中,上面8個圓形為存儲區域,下面4個圓形為計算通路。根據建模分析所有的連接情況如圖中的網絡,其中箭頭代表方向。該圖形左右對稱,分別代表兩個相同的處理單元。它們之間的交叉線表示在FFT最后一級運算時存在數據交換。經初步分析,優化后的網絡模型的數據復雜度僅為20。這樣通過將輸入緩沖存儲器劃分為8個模塊后,可以使設計的復雜度減少25.6倍,即降低為原來的4%以下。而且,隨著計算點數的增加,網絡的規模保持不變。根據這種方法得到單處理器和多處理器的復雜度如表1所示。?
?
?
4 實驗結果?
??? 根據優化模型分別設計相應的輸入緩存Input Buffer和輸出緩存Output Buffer。分別對這兩個單元進行控制信號仿真,仿真波形見圖5、圖6。?
?
?
?
??? 圖5、圖6中“rl”為行列變換轉換控制信號。對于輸出緩存,“we”和“en”分別為寫和讀控制信號。可以看出,在行變換和列變換的狀態下,分別對應16次讀寫信號。整個FFT的時間可以從緩存的工作狀態估算出來,即190μs～300μs之間,約110μs。?
??? 對于32×32點的二維FFT,每行/列變換需要分為5級運算,每次蝶形運算同時有4個數據到達。因此完成一次二維FFT共需要32×32×2×5/4=2 560個時鐘周期。工作在25MHz的主頻下,計算時間約為102μs。估算時間與仿真波形時間相近,可見整個計算過程中數據交換不存在網絡延時。?
??? 綜上所述,在FPGA片內實現并行計算時,存儲器采用FPGA內的“Block RAM”很難滿足多通道數據計算的需求,而分布式存儲模式則隨FFT計算點數增多而消耗過多資源。通過對特定FFT算法進行分析,改為分塊式存儲,將網絡模型進行了簡化,使存儲單元與處理器之間的數據通道數縮減為20,并且不隨FFT計算點數的增多而增多,將資源消耗控制在一定規模以內。整個并行FFT計算在Virtex XCV800上實現,經測試,計算時間僅為110μs,符合設計需求。?
參考文獻?
[1] 蘇濤,何學輝,呂林夏,等.實時信號處理系統設計[M].西安:西安電子科技大學出版社,2006?
[2] 布朗,施密特.空間太陽望遠鏡評估研究報告[M].中國科學院北京天文臺,1997.?
[3] 曾泳泓,成禮智,周敏.數字信號處理的并行算法[M].長沙:國防科技大學出版社,1999.?
[4] 胡廣書.數字信號處理[M].北京:清華大學出版社,1997.?
[5] 蔣增榮,曾泳泓,余品能.快速算法[M].長沙:國防科技大學出版社,1993.