摘 要: 在無線傳感器網(wǎng)絡(luò)中,傳感器節(jié)點的分布通常具有隨機(jī)性和密集性,監(jiān)測區(qū)域會出現(xiàn)覆蓋盲區(qū)或者覆蓋重疊。為此,推導(dǎo)出了無線傳感器最優(yōu)覆蓋模型計算最少節(jié)點個數(shù)的公式,對遺傳算法中的適應(yīng)度函數(shù)公式做了改進(jìn),將多重覆蓋率和覆蓋率的組合作為適應(yīng)度函數(shù)。根據(jù)遺傳算法的相關(guān)內(nèi)容和流程圖,利用遺傳算法對覆蓋策略做了仿真模擬,證明了所選用的方法的正確和優(yōu)越性。
關(guān)鍵詞: 無線傳感器網(wǎng)絡(luò);覆蓋;節(jié)點;遺傳算法
無線傳感器網(wǎng)絡(luò)WSN(Wireless Sensor Network)最早來源于軍事領(lǐng)域,1978年,卡內(nèi)基—梅隆大學(xué)就在美國國防高級研究項目組(DARPA)的資助下成立了分布式傳感器網(wǎng)絡(luò)工作組,專門研究以WSN為基礎(chǔ)的軍事監(jiān)視系統(tǒng)。該系統(tǒng)是傳感器技術(shù)、嵌入式計算技術(shù)、現(xiàn)代網(wǎng)絡(luò)及無線通信技術(shù)、分布式信息處理技術(shù)等的綜合應(yīng)用。
遺傳算法[1]GA(Genetic Algorithm)是模擬達(dá)爾文的遺傳選擇和自然淘汰生物進(jìn)化過程的計算模型,是一種通過模擬自然進(jìn)化過程搜索最優(yōu)解的方法。該算法最早是1975年由美國Michigan大學(xué)HOLLAND J教授提出來的,它是一種基于自然選擇和群體遺傳機(jī)理的高度并行、隨機(jī)、自適應(yīng)搜索算法。GA模擬了自然選擇和自然遺傳過程中發(fā)生的繁殖、交叉和基因突變現(xiàn)象,將每一個可能的解看作是群體中的一個個體,并將每一個個體編碼成字符串的形式,根據(jù)預(yù)定的目標(biāo)函數(shù)對每個個體進(jìn)行評價,給出一個適應(yīng)值,利用遺傳算子選擇、交叉、變異等過程對這些個體進(jìn)行組合,得到一群新個體。這一群新個體由于繼承了上一代的一些優(yōu)良性狀,所以明顯優(yōu)于上一代,這樣就逐步向著更優(yōu)解的方向進(jìn)化。
遺傳算法的主要優(yōu)點[2]是從代表問題可能潛在解集的一個種群開始并行操作的,而不是從一個初始點開始尋優(yōu),在一定程度上避免了搜索過程收斂與局部最優(yōu)解。其中一個種群則由經(jīng)過基因編碼的一定數(shù)目的個體組成。初代種群產(chǎn)生之后,按照適者生存和優(yōu)勝劣汰的原理,逐代演化產(chǎn)生出越來越好的近似解,在每一代根據(jù)問題域中個體的適應(yīng)度大小挑選個體,并借助于自然遺傳學(xué)的遺傳算子進(jìn)行組合交叉和變異,產(chǎn)生出代表新的解集的種群。
1 傳感器網(wǎng)絡(luò)最大覆蓋度的理想模型

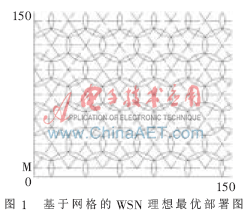
2 最優(yōu)部署模型節(jié)點數(shù)目公式
針對基于網(wǎng)格的WSN理想最優(yōu)部署圖,要求解所使用的最少節(jié)點數(shù)目Ns,并不能簡單地利用矩形長邊的節(jié)點個數(shù)與寬邊的節(jié)點個數(shù)相乘的積得出。因為由圖可以看出,每列的節(jié)點并不是一一對齊的,而是錯落排列的。根據(jù)右邊界位置的不同,區(qū)域中每行節(jié)點的數(shù)目也不同。在右邊界選擇可以改變的情況下,每行節(jié)點的數(shù)目有時相同有時不同。在推導(dǎo)節(jié)點數(shù)目Ns時,要對右邊界位于不同位置的情況分別進(jìn)行討論。在圖1的基礎(chǔ)上,為了便于對Ns進(jìn)行推導(dǎo),在原圖上增添了一些輔助線,作出求解最優(yōu)模型節(jié)點數(shù)目的分析圖,如圖2所示。將各點坐標(biāo)標(biāo)注其上,底邊橫坐標(biāo)從0開始,每隔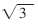 R依次標(biāo)注。左邊界從R/2開始,每隔3R/2依次標(biāo)注。把矩形各角依次標(biāo)注字母A、B、C、D。
R依次標(biāo)注。左邊界從R/2開始,每隔3R/2依次標(biāo)注。把矩形各角依次標(biāo)注字母A、B、C、D。
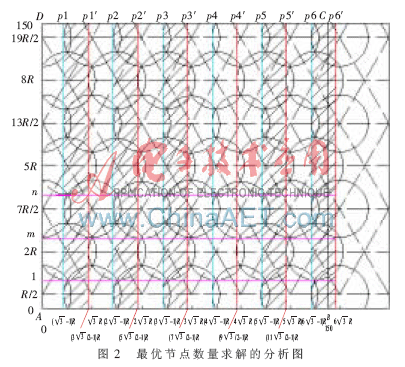
假設(shè)傳感器的感知半徑為R,被監(jiān)測矩形區(qū)域的長為L,寬為W,節(jié)點的行數(shù)為Ws,每行節(jié)點的數(shù)目為Ls,所有節(jié)點的數(shù)目為Ns。由圖2可以看出,由底邊向上算起,作第2行圓的下切線一條輔助線l,則底邊到l的距離為:



3 基于遺傳算法的最優(yōu)覆蓋策略
3.1 算法網(wǎng)絡(luò)模型

3.2 算法適應(yīng)度函數(shù)的求解
在監(jiān)測區(qū)域A的面積和傳感器的感知半徑一定的情況下,要使得節(jié)點數(shù)目最少且覆蓋度最大就是要使節(jié)點的分布盡量均勻,使得A內(nèi)的多重覆蓋的區(qū)域最小。所謂多重覆蓋區(qū)域[4]就是區(qū)域被兩個或兩個以上的傳感器節(jié)點覆蓋(覆蓋重數(shù)≥2)。因此,問題就轉(zhuǎn)化為在一定的覆蓋度的前提下,如果能使重疊面積最小,才能使用最少的傳感器節(jié)點且分布更加均勻。將具有多重覆蓋區(qū)域的面積設(shè)為So,將m個活動節(jié)點的面積相加即為展開后的總面積,則可以寫作m×Asi=mπRs2。對于監(jiān)測區(qū)域A有如下公式:
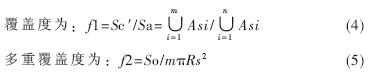
遺傳算法的適應(yīng)度函數(shù)[5]尤為重要,它的選擇直接關(guān)系算法最后的仿真實驗結(jié)果的準(zhǔn)確性,本模型統(tǒng)一由式(4)和式(5)兩個子函數(shù)構(gòu)成,并分別加上一個權(quán)值w1、w2,保證w1+w2=1,具體值可以由網(wǎng)絡(luò)設(shè)計者針對網(wǎng)絡(luò)的需要來決定。
F=w1×f1+w2(1-f2) (6)
遺傳算法就是要使得適應(yīng)度函數(shù)取最大值,而本文的目標(biāo)是使多重覆蓋度越小越好。因此對于f2函數(shù)應(yīng)該取相反值,可以得到(6)的適應(yīng)度函數(shù)。本文對遺傳算法的適值函數(shù)F做了改進(jìn),由面積占有率的函數(shù)表達(dá)式組成,式(5)比用節(jié)點的利用率[5]表示能獲得更好的效果。
4 仿真實驗
本實驗采用MATLAB 7.0對遺傳算法求解最優(yōu)覆蓋節(jié)點的方法進(jìn)行仿真。
設(shè)監(jiān)測區(qū)域為150×150的二維平面,傳感器的感知半徑R=15,初始群體隨機(jī)部署節(jié)點個數(shù)n=150,對于以上取值也滿足算法的要求,n遠(yuǎn)大于上面所計算出的Ns的數(shù)值。基于遺傳算法進(jìn)行求解,交叉概率一般在[0.4,0.99]中選取,因為在優(yōu)化過程中,交叉概率太大容易破壞種群中的優(yōu)良模式,太小雖然容易找到全局最優(yōu)解但進(jìn)化的速度太慢。變異概率選取一般是要求小于0.1。考慮以上原因,實驗選取交叉概率定為0.8,變異概率定為0.05,其目的就是既可以使節(jié)點最好的遺傳上一代的優(yōu)秀節(jié)點又防止節(jié)點出現(xiàn)節(jié)點局部最優(yōu)而使算法過早地收斂。根據(jù)遺傳算法的流程圖和以上實驗選取的參數(shù)因子,可以進(jìn)行算法的仿真。實驗中對每運行100代的相關(guān)數(shù)據(jù)(包括覆蓋度、多重覆蓋度、活動節(jié)點的個數(shù)等信息)都做了數(shù)據(jù)記錄,圖3(a)、3(b)、3(c)、3(d)依次為算法初始狀態(tài)、100、200和300代時的仿真圖,圖中所顯示的節(jié)點均是處于活動狀態(tài)節(jié)點的分布情況。本文選取運行代數(shù)為300代時作為最后的最優(yōu)部署圖。
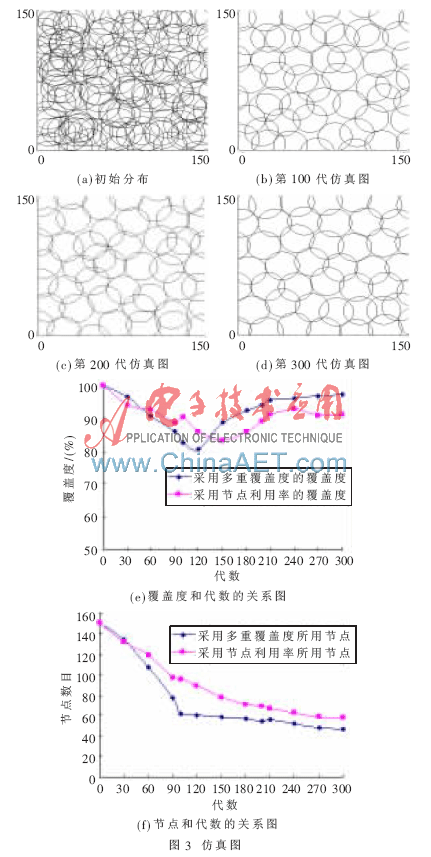
有些遺傳算法[6]是采用了覆蓋度和節(jié)點利用率作為適應(yīng)度函數(shù),從而達(dá)到在滿足覆蓋度要求的前提下使節(jié)點數(shù)目最少的目的。本文利用覆蓋度和節(jié)點利用率作為適應(yīng)度函數(shù)做了仿真實驗,在算法其他參數(shù)不變的前提下,將式(6)中以多重覆蓋率作為適應(yīng)度函數(shù)改為節(jié)點利用率的函數(shù),對實驗進(jìn)行重新模擬,同樣將實驗運行到第300代,并記錄了與上面實驗同樣的相關(guān)數(shù)據(jù)信息,分別從覆蓋度和活動節(jié)點這兩個數(shù)目與上面的實驗做比較分析,可以得到圖3(e)和3(f)的比較圖。
從圖3(e)中可以看出,隨著代數(shù)的增加,選用覆蓋率和多重覆蓋率的組合作為適應(yīng)度函數(shù)要比選用覆蓋率和節(jié)點利用率的組合作為適應(yīng)度函數(shù)所得到的覆蓋度高。并且改進(jìn)前的波形曲線有時有震蕩的現(xiàn)象,即得到的覆蓋度的結(jié)果會出現(xiàn)不穩(wěn)定的現(xiàn)象。改進(jìn)后的波形基本接近正態(tài)分布曲線,整個實驗過程很穩(wěn)定,不會出現(xiàn)覆蓋度忽高忽低的現(xiàn)象。
從圖3(f)中可以看出,隨著代數(shù)的增加,選用覆蓋率和多重覆蓋率的組合作為適應(yīng)度函數(shù)所用的節(jié)點數(shù)目要比選用覆蓋率和節(jié)點利用率的組合作為適應(yīng)度函數(shù)的節(jié)點淘汰速度要快。并且到300代時,改進(jìn)后的算法所用節(jié)點數(shù)目為47個,比改進(jìn)前的算法所用節(jié)點數(shù)目58個要少,所以改進(jìn)后的算法更加接近最優(yōu)模型中節(jié)點的數(shù)目。由圖3(e)、3(f)可以看出,在整個實驗的過程中,改進(jìn)后的算法的節(jié)點數(shù)目基本一直都小于改進(jìn)前的節(jié)點的數(shù)目,即使實驗運行到某一代停止了,改進(jìn)后的算法依然要明顯優(yōu)越于改進(jìn)前的算法。
本文改進(jìn)的遺傳算法通過以上仿真實驗數(shù)據(jù)對覆蓋度和節(jié)點數(shù)目的比較,可以明顯地看出,本實驗選用的多重覆蓋度代替節(jié)點利用率作為適應(yīng)度函數(shù)的遺傳算法是切實可行的。也達(dá)到了所要求的在滿足一定的覆蓋度的前提下,減少節(jié)點利用率的實驗?zāi)繕?biāo)。
參考文獻(xiàn)
[1] WARNEKE B, LAST M, LIEBOWITZ B. Smart dust: communicating with a cubic-millimeter computer[J]. IEEE Computer Magazine, 2001,34(1):44-51.
[2] CHONG Chee-Yee, KUMAR S P. Sensor Networks: Evolution[J]. Opportunities and Challenges Proceedings of the IEEE, 2003,9(8):1247-1256.
[3] SLIJEPCEVIC S, POTKONJAK M. Power efficient organization of wireless sensor networks[C]. In: Glisic S, ed. Proc. of the IEEE Conf.on Communications. Helsinki: IEEE Press,2001:472-476.
[4] ZHANG H, HOU J C. Maintaining sensing coverage and connectivity in large sensor networks[J]. Wireless Ad Hoc and Sensor Networks, 2005,1(1):89-124.
[5] 蔣杰,方力,張鶴穎,等.無線傳感器網(wǎng)絡(luò)最小連通覆蓋集問題求解算法[J].軟件學(xué)報,2006,17(2):175-184.
[6] 劉華峰,金士堯.三維無線傳感器網(wǎng)絡(luò)綜述[J].計算機(jī)應(yīng)用,2007,27.

