張大勇1，凌強1，計煒梁1，張俊斌2，徐酉亮2，熊遠波2，吳藝英2

　　（1.中國科學技術大學 自動化系，安徽 合肥 230027； 2.白城兵器實驗中心 輕武器部，吉林 白城 137001）

　　摘要：針對周期噪聲與窄帶噪聲，基于DSP硬件平臺，進行主動降噪系統設計與實現。主要工作為次級通道辨識、對算法定點化處理和基于DSP的實時降噪實現。所提出的定點化方法大大提高了定點DSP的運算速度，保證了降噪的實時性。其中降噪程序采用自適應算法中的前饋濾波X最小均方算法，DSP采用德州儀器公司的16位定點DSP TMS320VC5509A，使用TLV320AIC23B作為音頻處理芯片，取得了明顯降噪效果。

　　關鍵詞：主動降噪；濾波-X-最小均方算法；定點化

0引言

　　一直以來，噪聲污染都是各國十分關注的問題，同時它還是一個越來越嚴重的環境污染問題。交通噪聲、工業噪聲、建筑噪聲等給人的生理和心理健康帶來嚴重危害。這些噪聲使人聽力下降、易于疲勞、注意力下降、工作效率降低。因此，在噪聲越來越嚴重而人們越來越追求身體健康與生活質量的情況下，對噪聲的降低，在理論研究和工程實踐中都將具有廣泛的研究價值和廣闊的市場前景。

　　傳統的噪聲控制方法主要有吸聲、隔聲和使用消聲器等被動降噪（Passive Noise Control）方法［1］，其本質是利用聲波與材料的機械作用，使聲能變為熱能等其他形式的能量以減少噪聲。隨著信號處理技術和電子技術的高速發展，主動噪聲控制（Active Noise Control）有了明顯的進展［2］。其原理是根據2個聲波相消性干涉或聲波輻射抑制的方法，通過人為地制造1個控制聲源 (次級聲源)，使其發出的聲音與原來的噪聲源(初級聲源)輻射噪聲大小相等、相位相反，使兩者作用結果互相抵消，從而達到降噪的目的。本文即采用主動降噪思想，使用前饋濾波X最小均方（FXLMS）算法［3 4］，并借助DSP平臺構造一個主動降噪系統。

　　本文首先通過DSP平臺產生白噪聲對次級通道進行辨識，然后對浮點程序進行定點化處理，最后通過揚聲器產生反噪聲來抵消外界噪聲。針對單頻噪聲和窄帶噪聲進行降噪處理，能夠在C55x系列DSP平臺上實現實時性；而且通過對浮點算法進行定點化處理，大大提高了在DSP平臺上的運算速度；通過提高采樣率，可以對最高7 kHz的高頻噪聲進行降噪，以適應噪聲可能存在的變化。

1次級通道辨識

　　前饋X-濾波最小均方算法（FXLMS）算法即在基本的LMS算法的基礎上考慮了次級通道S(z)的影響。如圖1所示，次級通道指從產生聲音信號并通過揚聲器輸出，到通過拾音裝置采集并獲得聲音信號的通道S(z)。原始噪聲d(n)疊加在自適應濾波器輸出的噪聲抵消信號y(n)上，誤差信號e(n)被誤差麥克風檢測到。但y(n)到e(n)的聲音次級通道函數S(z)會改變噪聲抵消信號y(n)，因此，需要對次級通道進行建模，構造S^(z)對次級通道進行補償。　

　　具體的次級通道包括揚聲器中的D/A轉換器、重構濾波器、功放，揚聲器到拾音裝置聲器之間的通道，拾音裝置中的誤差傳聲器、前置放大、抗混疊濾波器以及A/D轉換器。設定次級通道為30階，為了更準確地辨識次級通道，本文根據最小均方算法進行運算。

　　如圖2所示，次級通道的辨識過程如下。

　　（1）通過DSP平臺產生白噪聲y(n)并由音頻編解碼芯片aic23讀取，然后通過抵消揚聲器發出白噪聲。

　　（2）通過抵消麥克風采集步驟（1）中抵消揚聲器發出的白噪聲信號。

　　（3）利用步驟（1）中的白噪聲信號計算自適應濾波器的輸出信號r(n)，求取公式如下：

　　式中u(n)表示步驟（1）產生的白噪聲信號序列，si(n)表示自適應濾波器系數，n為當前時刻，M為濾波器階數，i為濾波器的階數序號。

　　（4）計算誤差信號，其求取公式如下：

　　e′(n)=v(n)－r(n)(2)

　　式中v(n)為誤差麥克風采集到的聲音信號，r(n)為步驟（3）中自適應濾波器的輸出。

　　（5）利用最小均方準則更新自適應濾波器的系數，其求取公式如下：

　　si(n+1)=si(n)+μe′(n)u(n－i),

　　i=1,…,M－1(3)

　　式中：迭代步長μ取值0.05，濾波器階數M取30階。

　　（6）判斷迭代次數是否大于T（T取10 000）次，當迭代次數大于T時，停止迭代，完成對次級通道的辨識，此時就得到了次級通道的系數。

2對浮點程序定點化處理

　　現有的DSP處理器中，無論從運算速度還是設備成本看，定點處理器較浮點處理器都有一定的優勢［5］，因此本設計采用了C55x系列的16 bit定點DSP TMS320C5509A。但是由于定點DSP處理浮點數據比較慢，因此對浮點程序進行了定點化處理。定點化可以直接著手進行，也可以在完成浮點算法的基礎上對降噪程序進行改造，本設計采用后者。

　　采用定點數表示實際的浮點數，浮點數和定點數的轉換公式如下：

　　浮點數(X)轉換為定點數:

　　XQ=(int)X*2Q（4）

　　定點數(XQ)轉換為浮點數:

　　X=(float)XQ*2－Q（5）

　　對浮點算法定點化時，加減法的運算規則不變，乘法運算時要將乘積除以2n，而乘除法運算時要將被除數乘以2n，由于對2n進行乘除運算均可以用移位運算替代，因此可以大大提高運算速度。

　　不同的Q格式所表示的數的范圍不同，精度也不同。Q越大，數值范圍越小，但精度越高。例如，Q0(Q=0)的數值范圍是-32 768~+32 767，其精度是1，而Q15的數值范圍為-1~0.999 969 5，精度為1/32 768=0.000 030 51，因此數據范圍和精度是一對矛盾。

　　如圖3所示，本設計中針對浮點程序的定點化處理流程如下。

　　（1）定標方式選取為Q15。

　　（2）利用式X15=(int)X*215將已知的浮點數據轉換為定點數據。所謂已知的數據是指能直接采集到的輸入信號（如采集麥克風采集到的噪聲信號，誤差麥克風采集到的誤差信號），以及一些需要設定的參數（如迭代步長μ）。

　　（3）將需要計算才能得到的浮點數據求取公式進行定點化改造。例如浮點算法中e′(n)的求解公式為：

　　e′(n)=v(n)－r(n)

　　定點化后e′(n)的求解公式為:

　　e′15(n)=v15(n)－r15(n)（6）

　　r15 (n)為反噪聲信號r(n)的定點化形式,v15 (n)為誤差麥克風采集的誤差信號v(n)的定點化形式，可由步驟（2）求得，即：

　　v15(n)=(int)v*215(7)

　　(4)用定點化算法對次級通道進行再次辨識并測得次級通道的整形系數。通過DSP平臺產生白噪聲，并通過噪聲抵消揚聲器輸出，對次級通道進行辨識，得到次級通道整形系數。

　　(5)判斷數據精度是否滿足要求。將步驟（4）中所測的次級通道的系數與浮點算法得到的系數進行比較。如果次級通道的整形系數除以215后與浮點系數的誤差在-0.003~0.003之間，則數據精度符合要求，定點化結束。如果不滿足這個條件，就需要改變定標格式對定點化進一步改進，進入步驟（6）。

　　（6）使用Q16~Q31定標方式，并進入步驟（2）再次進行定點化改造。

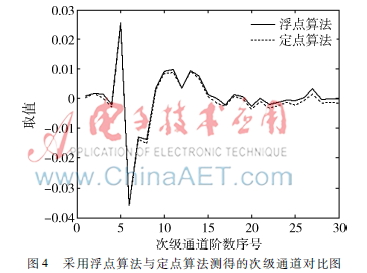
　　采用浮點算法與定點算法測得的次級通道對比圖如圖4所示，圖中實線表示浮點算法得到的次級通道的浮點系數。由于定點算法中次級通道采用的是Q15格式，因此虛線是定點算法學習到的系數除以215之后的數值，次級通道設定為30階，采樣率為1 kHz。可以發現，兩條曲線幾乎重合，它們的最大誤差是0.001 9，在-0.003~0.003之間。因此采用Q15定標方法的定點算法后，精度滿足要求。

3利用揚聲器產生反噪聲來抵消外界噪聲

　　定點程序的精度滿足要求時，即開始進行降噪的階段。對于外界單頻與窄帶噪聲，通過抵消揚聲器發出反噪聲，可以達到良好的降噪效果。

　　如圖5所示，降噪實現過程如下。

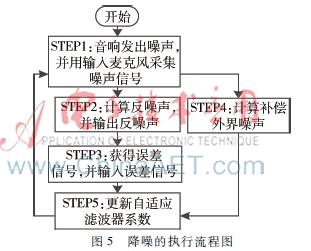
　　（1）由音響輸出噪聲并通過采集麥克風采集該噪聲信號。

　　（2）利用步驟（1）采集的噪聲信號計算需要的反噪聲信號y(n)，并利用抵消揚聲器發出，其求取公式為：

　　式中x(n)為在n時刻采集到的外界噪聲，wi(n)為自適應降噪濾波器在n時刻的系數，N為自適應降噪濾波器的階數。

　　（3）由誤差麥克風采集誤差噪聲信號e(n)。

　　（4）計算利用步驟（1）中采集到的噪聲信號經過次級通道進行補償后的值，其求取公式為：

　　式中ci(n)次級通道的系數，x(n)為在n時刻采集到的外界噪聲，M為該自適應濾波器系數。

　　(5)利用最小均方準則更新自適應降噪濾波器的系數wi(n)，其求取公式如下：

　　wi(n+1)=wi(n)－μ*e(n)*x′(n－i)

　　i=0,…,N－1(10)

　　式中e(n)為步驟（3）中采集得到的誤差噪聲信號，i為濾波器階數序號，μ為迭代步長，x′(n)為步驟（4）中得到的噪聲信號的補償值。通過不斷調節自適應濾波器系數濾就可以對外界噪聲進行實時降噪處理。

4實驗結果

　　利用音響發出7 kHz音頻作為外界噪聲，利用CCS軟件的Graph功能對得到的數據進行作圖并截圖，采樣率設為16 kHz，結果如圖6和圖7所示。由圖6與圖7可以看出，降噪前噪聲幅值為1 300，降噪后最大值為300，換算為降噪比為：

　　20lg(1 300/300)=12.7dB

　　降噪效果比較明顯。同時，噪聲在開啟降噪到迭代250次穩定，需要的時間是：

　　250/16000=0.015 625 s

　　由于人耳的反應時間是0.1 s左右，因此降噪可以取得很好的實時效果。

5結論

　　本文利用前饋FXLMS算法進行ANC程序設計，提出了一種針對浮點FXLMS算法定點化的方法，通過在德州儀器公司的定點DSP C5509A上實施，大大提高了定點DSP的運算速度，使降噪可以具有實時性；同時，還可以對高頻噪聲取得良好的降噪效果。為了增強系統的性能，在今后的工作中可以考慮限制自適應濾波器系數的波動范圍［4］，或者采用變步長的改進算法［6 7］,以增強系統的魯棒性。

參考文獻

　　［1］ 周亞麗. 有源噪聲與振動控制［M］. 北京：清華大學出版社, 2014.

　　［2］ 陳克安. 有源噪聲控制［M］. 北京：國防工業出版社, 2003.