摘 要: 針對基本果蠅優化算法在求解高維函數時存在求解精度低、迭代收斂速度較慢等問題,提出一種基于差分演化的果蠅優化算法。該算法將差分演化策略融合到果蠅優化算法中,對每代產生的群體進行變異、交叉、選擇操作,增加種群的多樣性,使其能更快、更有效地求解高維函數問題。對12個基準函數進行了仿真驗證,結果表明,與基本的果蠅優化算法和差分演化算法相比,新算法在收斂速度、求解精度上都具有明顯的優越性。
關鍵詞: 果蠅優化算法;差分演化;多樣性
0 引言
果蠅優化算法(Fruit Fly Optimization Algorithm,FOA)是一種新的全局優化進化算法[1]。該算法源于對果蠅覓食行為的模擬[2],由于該算法參數較少,結構簡單,實現容易,因而一經提出便得到了一些學者的研究和應用[3-6]。然而,果蠅優化算法和其他全局優化算法一樣,受參數的影響很大,也容易陷入局部最優。目前關于改善果蠅優化算法性能的研究成果相對較少,迫切需要展開更深入研究。
果蠅優化算法中所有個體都向最優的位置聚集,這一行為導致種群多樣性的丟失,特別是對于高維多極值復雜優化問題,易出現求解精度低、迭代收斂速度較慢等問題。針對這一問題,本文將差分演化策略融合到果蠅優化算法中,對每代產生的群體進行若干次的變異、交叉、選擇操作,從而增加種群的多樣性,使其更快、更有效地求解復雜函數問題。
1 基本果蠅優化算法和差分進化算法
1.1 基本的果蠅優化算法
果蠅優化算法是一種基于果蠅覓食行為推演出的尋求全局優化的新方法。果蠅本身在感官知覺上優于其他物種,尤其是在嗅覺與視覺上。首先果蠅利用嗅覺搜集空氣中的氣味,然后飛向食物位置附近,再利用視覺發現食物與同伴聚集的位置,并且往該方向飛去。
依據果蠅搜索食物特性,將果蠅優化算法歸納為以下幾個必要的步驟[2]:
(1)初始化種群。給定種群規模Sizepop和最大迭代數Maxgen,在搜索空間中隨機初始化果蠅群體位置X_axis和Y_axis;
(2)設置果蠅個體利用嗅覺搜尋食物的隨機方向與距離:
Xi=X_axis+RandValue(1)
Yi=Y_axis+RandValue(2)
式中,RandValue為搜索距離。
(3)計算個體與原點之距離Disti和味道濃度判定值Si,其值為距離Disti的倒數:

Si=1/Disti(4)
(4)將味道濃度判定值Si代入味道濃度判定函數(或稱為適應度函數),求出果蠅個體位置的味道濃度Smell(i)(適應值):
Smell(i)=Function(Si)(5)
(5)找出該果蠅群體中味道濃度最佳的果蠅個體(最小化問題):
[bestSmell bestindex]=min(Smell(i))(6)
式中,bestSmell為最佳味道濃度值;bestindex為最佳位置序列。
(6)記錄并保留最佳味道濃度值bestSmell與其X、Y坐標,這時果蠅群體利用視覺向該位置飛去:
Smellbest=bestSmell(7)
X_axis=X(bestindex)(8)
Y_axis=Y(bestindex)(9)
(7)進入迭代尋優,重復執行步驟(2)~(5),并判斷最佳味道濃度是否優于前一迭代最佳味道濃度且當前迭代次數小于最大迭代次數,若是則執行步驟(6)。
1.2 差分進化算法
差分進化(Differential Evolution,DE)算法[7]是一種隨機的并行直接搜索算法。其基本原理:對個體進行方向擾動,以達到使個體函數值下降的目的。通過對種群中兩個隨機選擇的不同向量來干擾現有向量,得到臨時種群;對臨時種群進行評價,計算臨時種群中每個個體的目標函數值;對臨時種群進行比較、選擇,選取目標函數值小的新種群。DE算法以差分策略為主要特征,不同的差分策略實現不同的變異操作。本文選取rand/1/bin策略。如下所示:
(1)變異操作。選取rand/1/bin策略。從種群中隨機選擇3個不同個體xp,xq,xr,則:
vi(t)=xp+F(xq-xr)(10)
式中,F為縮放因子。
(2)交叉操作。此操作可以增加種群的多樣性。如下所示:
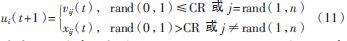
式中,CR為交叉概率,CR∈[0,1];rand(1,n)為[1,n]之間的隨機整數。
(3)選擇操作。由適應值函數對向量進行比較選擇,如下所示:
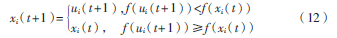
2 融合差分算法的混合果蠅算法
在果蠅優化算法迭代過程中,一旦發現最優個體,種群中的所有個體都向這個最優位置聚攏,這一特性減少了種群的多樣性。如果該個體不是全局最優,極易使種群陷入局部最優。本文提出的融合差分演化的混合果蠅算法(簡稱DFOA),結合差分演化策略,對每代產生的群體進行若干次差分演化操作(變異、交叉、選擇),增加種群的多樣性,更快、更有效地求解極值。
具體步驟如下:
(1)初始化算法所需的參數;
(2)按式(1)、(2)初始化果蠅群體;
(3)按式(3)~(5)對果蠅個體進行操作;
(4)按照式(6)得到最佳的果蠅位置和最佳味道濃度值;
(5)對果蠅種群按照式(12)~(14)進行m代的差分演化操作,將得到的個體作為最佳果蠅個體;
(6)記錄并保留新的最佳味道濃度值Smellbest與X、Y的坐標X_axis、Y_axis。
(7)重復執行步驟(2)~(6)的操作,直到達到最大迭代次數,或者達到目標精度要求。
從步驟(5)中可以知道,差分演化代數m可以不同。種群中差分進化代數m表明執行變異、交叉、選擇操作的次數,這些操作決定了種群的變異次數,與種群的多樣性有關。
3 實驗及結果分析
3.1 實驗設計

為了驗證本文DFOA算法的性能,設計了3類測試函數:(1)DE優化實驗;(2)DFOA優化實驗;(3)FOA優化實驗。實驗選用12個常用的優化算法比較基準函數(求解最小值)。函數表達式、搜索區間、理論極值如表1所示。其中F7、F10表達式如下所示:

3.2 對比實驗與結果分析
3.2.1固定迭代次數,評估算法性能
本文將迭代次數固定為1 000,函數維數為30,種群個數設置為50,差分迭代次數為10。參數F取為0.5,CR取為0.1~0.9之間的自適應交叉概率。記錄DE、FOA和DFOA三種算法經過20次獨立運行后,12個基準測試函數的運行結果,如表2所示。
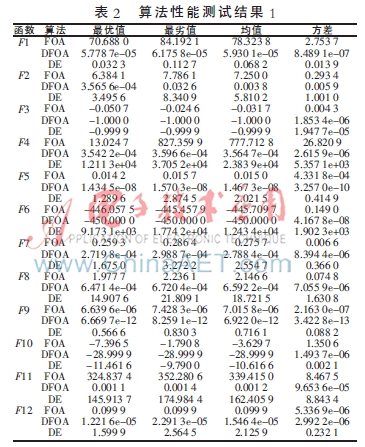
從表2中可以看出,DFOA不論是在最優值、優化均值和穩定性上都比FOA和DE算法好很多。對于復雜問題,改進的算法在精度、收斂速度上都有顯著的提高。
3.2.2 差分迭代次數對算法的影響
種群中差分進化代數m表明執行變異、交叉、選擇操作的次數,這些差分操作決定了種群的變異次數,與種群的多樣性有關,因此關系到DFOA的性能。不同的差分迭代次數使算法的結果也不相同。參數的設置如上述所示。獨立運行20次結果如表3所示。

由表3可知,m值越大,算法的收斂精度就越高,但缺點是程序執行的速度會變慢。因此,必須考慮到優化問題的復雜程度,適當選擇m值。
4 結束語
基本的果蠅優化算法在尋優過程中,所有個體都向最優值聚攏,這一行為導致種群多樣性的丟失,特別是對于高維復雜優化問題,易出現求解精度低、迭代收斂速度較慢等問題。針對這一問題,本文將差分演化策略融合到果蠅優化算法中,對每代產生的群體進行若干次差分演化操作,增加種群的多樣性。并通過12個基準函數進行仿真驗證,結果表明:相較于FOA、DE,新算法能更快、更有效地求解復雜函數問題。
參考文獻
[1] PAN W T. A new fruit optimization algorithm: taking the financial distress model as an example[J]. Knowledge-Based Systems, 2012,26(1):69-74.
[2] 潘文超.果蠅最佳化演算法[M].臺北:滄海書局,2011:10-12.
[3] XING Y F. Design and optimization of key control characteristics based on improved fruit fly optimization algorithm [J]. Kybernetes, 2013, 42(3): 466-481.
[4] LI H Z, GUO S, Li C J, et al. A hybrid annual power load forecasting model based on generalized regression neural network with fruit fly optimization algorithm[J]. Knowledge-based systems,2013,37(1):378-387.
[5] 劉成忠,黃高寶,張仁陟,等.局部深度搜索的混合果蠅優化算法[J].計算機應用,2014(4):1060-1064.
[6] 韓俊英,劉成忠.自適應調整參數的果蠅優化算法[J].計算機工程與應用,2014(7):50-55.
[7] STORN R, PRICE K. Differential evolution—a simple and efficient adaptive scheme for global optimization over continuous spaces[J]. Technical Report, International Computer Science Institute, 1995(8): 22-25.

